Экспериментальная установка

Общий вид прибора для измерения вязкости по методу Стокса показан на рис. 3. Для измерений используется стеклянный цилиндрический сосуд В, наполненный исследуемой жидкостью 11 (раствор глицерина). Диаметр сосуда ≈3 см, длина ≈40 см. На стенках сосуда нанесены три метки на расстоянии ≈10 см друг от друга. Верхняя метка должна располагаться ниже уровня жидкости с таким расчетом, чтобы скорость шариков к моменту прохождения этой метки успевала установиться. Измеряя расстояние между метками с помощью линейки, а время падения с помощью секундомера, определяют скорость шарика . Сам сосуд В помещён в рубашку Д, омываемую водой из термостата. В установившемся режиме температура жидкости 11 равна температуре воды в термостате.

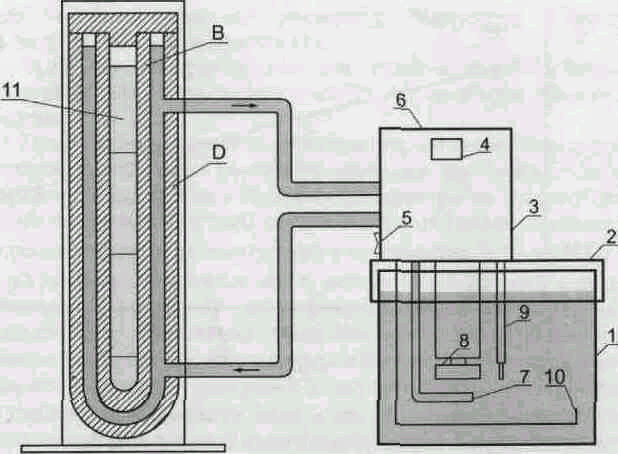
Рис. 3. Общий вид установки для измерения вязкости по методу Стокса

Радиусы шариков измеряются отсчётным микроскопом. Для каждого шарика рекомендуется измерить несколько различных диаметров и вычислить среднее значение. Такое усреднение целесообразно, поскольку в работе используются шарики, форма которых может несколько отличаться от сферической. Плотность используемых стеклянных и стальных шариков известна (см. «Приборы, оборудование и их характеристики»).

Опыты по определению вязкости жидкости проводятся при нескольких температурах в интервале от комнатной до 50–60°С.

Плотность жидкости определяют для каждого значения температуры по графику (рис. 4).

Для точного задания и поддержания требуемой постоянной темпе­ратуры при проведении измерений в данной работе используется водяной термостат (описание его работы см. приложение 5), который состоит из резервуара 1, крышки 2 и блока управления 3. На передней стороне блока управления расположен световой индикатор 4 контроля температуры. На задней стороне – сетевой выключатель 5. На верхней крышке находятся три кнопки управления 6. В нижней части блока смонтирован нагреватель 7, крыльчатка водяного насоса 8, датчик температуры и уровня воды 9. На блоке расположены две трубки, которыми термостат соединён с рубашкой Д. Другие две трубки – для пропускания водопроводной воды через змеевик 10 (для охлаждения термостата).

Рис. 4. Зависимость плотности раствора глицерина от температуры

Теория эксперимента

По формуле Стокса (4) можно определить скорость установившегося падения шара в вязкой жидкости. Тяжелый шар в вязкой жидкости лишь в самый первый момент начнет падать ускоренно; по мере же возрастания скорости его падения возрастает и сила трения F, которая начинает уравновешивать силу тяжести , действующую на шар. Когда такое уравновешивание сил достигнуто, шар падает равномерно с постоянной скоростью .

Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют три силы (рис. 5):

Х

Рис. 5. Силы, действующие на шарик, движущийся в жидкости

1. Сила тяжести , где – плотность материала шарика, V – объем шарика, а g – ускорение свободного падения;

2. Сила Архимеда , где – плотность жидкости;

3. Сила вязкости (сила Стокса), зависящая от скорости , где r – радиус шарика, – его скорость.

Найдём уравнение движения шарика в жидкости. По второму закону Ньютона

.

В проекции на ось Х (рис. 5) при установившемся падении шарика (а=0)

.

Подставляя в это равенство выражения для сил, получим

. (5)

Отсюда

, (6)

Во втором равенстве мы подставили значение объема шарика .

Величина

(7)

называется временем релаксации. Для установления скорости необходимо, чтобы время падения шарика в жидкости более чем в три раза превосходило время релаксации.

Измеряя на опыте установившуюся скорость падения шариков , и величины , можно определить вязкость жидкости по формуле, следующей из (6):

. (8)

Указания. Описанная выше методика определения вязкости основана на формуле Стокса и правильна лишь в том случае, если выполнены предположения, сделанные при выводе этой формулы. Самым надежным способом проверки теории является следующий. Шарики с разными радиусами движутся в жидкости с разными скоростями и с разными временами релаксации. Если во всем диапазоне встречающихся в работе скоростей и времен релаксации вычисленные по формуле (8) значения оказываются одинаковыми, то формула (4) правильно передает зависимость сил от радиуса шарика. Зависимость (или независимость) от r служит чувствительным индикатором правильности теории и надежности эксперимента.

Результаты опыта имеет смысл обрабатывать лишь в том случае, если значения не обнаруживают систематической зависимости от r. Если такая зависимость наблюдается, то чаще всего это связано с влиянием стенок сосуда. В этом случае вместо формулы (8) следует использовать более точную формулу

, (9)

где R — радиус сосуда. Для небольших шариков отличие (9) от (8) лежит в пределах точности эксперимента и может не приниматься во внимание. (Формула (9) верна для шариков, движущихся вблизи осевой линии сосуда, при условии r<<R.)

Полезно исследовать применимость формулы Стокса не только экспериментально, но и теоретически. При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Как известно, характер обтекания определяется значением числа Рейнольдса

. (10)

Обтекание является ламинарным лишь при не очень больших значениях R_e (<10). По результатам опыта следует вычислить числа Рейнольдса для разных размеров шариков и различных температур жидкости. Полезно также вычислить время релаксации .