Контрольные вопросы

1. Что называется теплопроводностью твердого тела?

2. Что называется коэффициентом теплопроводности твердого тела?

3. Почему в работе вместо 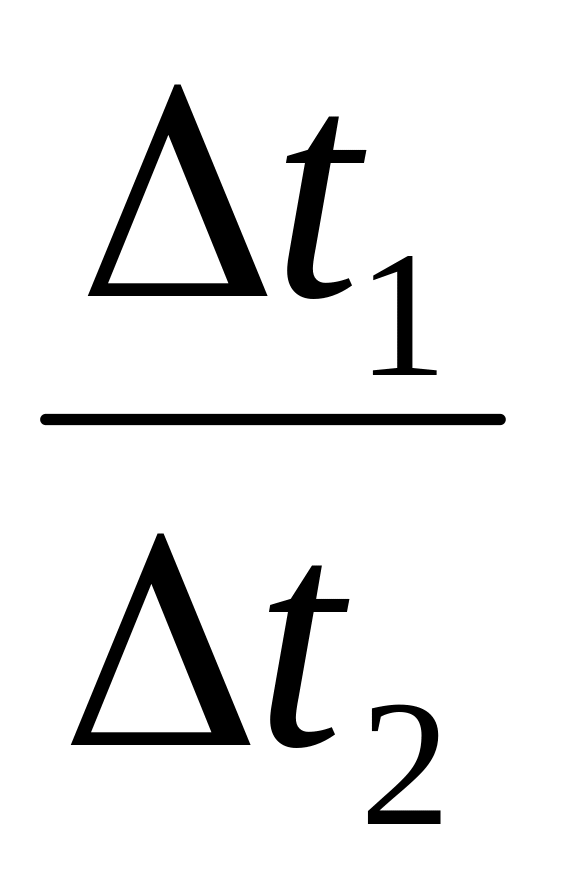подставляется величина .

4. Резину в эксперименте заменили войлоком, как изменится исследуемого образца.

5. Почему снятие показания приборов производится после прохождения некоторого времени после включения установки?

6. Изменится ли значение , если площадь образца увеличить вдвое.

7. Изменится ли значение , если толщину пластины увеличить вдвое.

Лабораторная работа №4

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

ПО МЕТОДУ СТОКСА

Цель работы: Познакомиться с классическим методом определения коэффициента вязкости жидкости (методом Стокса), определить зависимость этого коэффициента от температуры и на этой основе определить энергию активации жидкости.

Литература:

1. Радченко И.В. Молекулярная физика. – М.: Наука, 1965, гл. 15, §§ 1–4.

2. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. I. Физические основы механики. Молекулярная физика. Колебания и волны. – М.: Физматгиз, 1961, гл. IX, §§ 78, 95.

3. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 704 с.

4. Введение в технику эксперимента/ Составитель: Беленко И.А. –   БелГУ, 2004. – 124 с.

Приборы, оборудование и их характеристики:

1. Стеклянный цилиндр с исследуемой жидкостью (80-ти %-ный водный раствор глицерина) с нанесенными на нем метками:

Диаметр сосуда 3 см, длина 40 см;

Расстояние между двумя ближайшими метками ≈10 см;

2. Термостат TW – 2.03;

3. Электронный секундомер «Интеграл ЧС – 01»;

4. Отсчётный микроскоп;

5. Набор стальных и стеклянных шариков (диаметром около 1 мм):

плотность стальных шариков 7,6·10³ кг/м³;

плотность стеклянных шариков 2,5·10³ кг/м³.

Теория метода

По своим свойствам жидкости сходны как с газами, так и с твердыми телами. Подобно газам жидкости принимают форму сосуда, в котором они находятся. Подобно твердым телам они обладают сравнительно большой плотностью, с трудом поддаются сжатию.

Двойственный характер свойств жидкостей связан с особенностями движения их молекул. В газах молекулы движутся хаотично, в их расположении отсутствует порядок. В кристаллических твердых телах частицы колеблются около определенных положений равновесия – узлов кристаллической решетки. В жидкостях, как и в кристаллах, каждая молекула находится в потенциальной яме электрического поля, создаваемого окружающими молекулами. Молекулы колеблются со средней частотой, близкой к частоте колебаний атомов в кристаллических телах (~10¹² Гц), и с амплитудой, определяемой размерами объема, предоставленного им соседними молекулами. Глубина потенциальной ямы в жидкостях больше средней кинетической энергии колеблющейся молекулы, поэтому молекулы колеблются вокруг более или менее стабильных положений равновесия. Однако у жидкостей различие между этими двумя энергиями невелико, так что молекулы нередко выскакивают из «своей» потенциальной ямы.

В отличие от твердых тел, жидкости обладают «рыхлой» структурой. В них имеются свободные места – «дырки», благодаря чему молекулы могут перемещаться, покидая свое место и занимая одну из соседних дырок. Таким образом, молекулы медленно перемещаются внутри жидкости, пребывая часть времени около определенных мест равновесия и образуя как бы нерегулярную и меняющуюся со временем пространственную решетку. На современном языке принято говорить, что в жидкости присутствует ближний, но не дальний порядок, расположение молекул более или менее упорядочено лишь вблизи каждой молекулы, но становится незаметным на расстоянии.

Как уже отмечалось, для того чтобы перейти в новое состояние, молекула должна преодолеть участки с большой потенциальной энергией, превышающей среднюю тепловую энергию молекул. Для этого тепловая энергия отдельной молекулы должна (вследствие флюктуаций) возрасти по сравнению со средним значением на некоторую величину W, называемую энергией активации. Вследствие этого переходы молекул из одного положения равновесия в другое происходят сравнительно редко и тем реже, чем больше энергия активации.

Количество молекул, имеющих энергии больше W, в соответствии с формулой Больцмана экспоненциально зависит от W. Я.И. Френкель показал, что температурная зависимость вязкости жидкости должна выражаться формулой

. (1)

Второй множитель меняется с температурой гораздо быстрее, чем первый, а сама формула носит приближенный характер. Поэтому без большой ошибки первый множитель можно заменить константой:

. (2)

Из формулы (2) следует, что вязкость жидкости при повышении температуры должна резко уменьшаться. Если отложить на графике логарифм вязкости в функции 1/Т, то согласно (2) должна получиться прямая линия, по угловому коэффициенту которой можно определить энергию активации молекулы W исследуемой жидкости. Экспериментальные исследования показывают, что в небольших температурных интервалах эта формула неплохо описывает изменение вязкости с температурой. При увеличении температурного интервала согласие получается плохим, что представляется вполне естественным, поскольку формулы (1) и (2) выведены при очень грубых предположениях.

Во всех реальных жидкостях при перемещении одних слоев относительно других возникают более или менее значительные силы трения. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряю­щая сила. Наоборот, со стороны слоя, движущегося медленнее, на более быстрый слой действует задерживающая сила. Эти силы, носящие название сил внутреннего трения, направлены по касательной к по­верхности слоев. Величина силы внутреннего трения тем больше, чем больше площадка поверхности слоя, которую мы рассматриваем, и зависит от того, насколько быстро меняется скорость те­чения жидкости при переходе от слоя к слою.

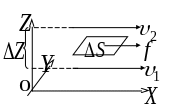
Рис. 1. Возникновение сил вязкого трения.

Пусть два слоя (рис. 1), отстоящих друг от друга на расстоянии , текут соответственно со скоростями и . Положим . Направление, в котором отсчитывается расстояние между слоями , перпендикулярно к ско­рости течения слоев. Величина , которая показывает, как быстро меняется скорость при переходе от слоя к слою, носит название градиента скорости. Сила внутреннего трения пропорциональна градиенту скорости, так что

(3)

Величина , зависящая от природы жидкости, называется коэф­фициентом внутреннего трения или коэффициентом вязкости жидкости. Чем больше коэффициент вязкости, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают.

Рассмотренное нами течение жидкости носит название ламинар­ного (по-латыни – слоистого), так как слои жидкости как бы сколь­зят друг относительно друга. При движении жидкости по трубе с увеличением скорости течение теряет ламинарный характер и ста­новится беспорядочным. Возникают составляющие скорости, перпен­дикулярные к оси трубы. В каждой точке жидкости происходят беспорядочные отклонения вектора скорости от его среднего значе­ния. Такое движение носит название турбулентного. Переход от ламинарного к турбулентному движению в трубах или каналах ведет к резкому возрастанию сопротивления.

При обтекании вязкой жидкостью тел с увеличением скорости течение меняет свой характер и становится завихренным. Поток жидкости, отрывающийся от поверхности обте­каемого тела, распадается на отдельные вихри. Вихри, образующиеся позади тела (рис. 2), уносятся потоком и постепенно затухают.

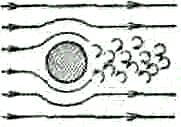Рис. 2. Образование вихрей

Таким образом, при движении тела в вязкой среде возникает сопротивление. Происхождение этого сопротивления двояко. При малых скоростях и удобообтекаемой форме тела, когда не возникает вихрей, сила сопротивления непосредственно обусловлена вязкостью жидкости. Слой жидкости, прилегающий к твердому телу, «прилипает» к его поверхности и увлекается им полностью. Следующий слой увлекается за телом с меньшей скоростью.

Для определения вязкости жидкости в данной работе используется метод Стокса, основанный на измерении скорости свободного падения шарика в жидкости. Суть его заключается в следующем.

На всякое тело, двигающееся в вязкой жидкости, действует сила сопротивления. В общем случае величина этой силы зависит от многих факторов: от вязкости жидкости, от формы тела, от характера обтекания и т. д. Стоксом было получено строгое решение задачи о ламинарном (безвихревом) обтекании шарика безграничной жидкостью. В этом случае сила сопротивления F определяется формулой

, (4)

где – коэффициент вязкости жидкости, – скорость шарика, r – его радиус.