10. Химические источники тока

Химическими источниками тока (ХИТ) называются устройства, в которых энергия Гиббса пространственно разделенных окислительно-восстановительных процессов превращается в электрическую энергию. Все используемые на практике ХИТ делятся на две группы:

– гальванические элементы (первичные ХИТ), позволяющие однократное использование их активных материалов;

– аккумуляторы (вторичные ХИТ), работоспособность которых после разряда может быть восстановлена зарядкой от внешнего источника постоянного тока.

Конструктивное выполнение ХИТ может быть разнообразным, но в принципе они состоят из двух электродов – проводников электричества первого рода, разделенных электролитом, то есть проводником второго рода. Знаки электродов и общепринятые их названия соответствуют протекающим на них окислительному (анод, минус) и восстановительному (катод, плюс) процессам. При работе ХИТ получающиеся на аноде электроны «перетекают» по внешней цепи к катоду. Природа и направление потока ионов в электролите работающего ХИТ определяется в каждом конкретном случае. Главной величиной, характеризующей служебные характеристики ХИТ, является электродвижущая сила (ЭДС, Е). Она определяется разностью потенциалов катода и анода

,

каждый из которых рассчитывается по уравнению Нернста (см. главу 8). Рассмотрим несколько примеров гальванических элементов и аккумуляторов.

Простейший пример – медно-цинковый элемент

(10.1)

изобретенный в 1836 г. английским ученым и изобретателем Д.Ф. Даниелем. Этот элемент – первый в мире устойчивый источник постоянного электрического тока (рис. 3). Металлические пластины (цинк и медь) опущены в водные растворы сернокислых солей. Электролиты разделены полупроницаемой перегородкой (мембрана, солевой мостик), исключающей перемешивание электролитов, но позволяющей проходить ионам . Катодный процесс в этом элементе – восстановление меди из раствора сернокислой меди

;

Рис. 3. Схема элемента Даниеля–Якоби

равновесный электродный потенциал медного катода (при раздвинутой внешней цепи, I = 0)

(10.2)

где стандартный электродный потенциал (25 °С, = 1) = +0,337 В; – активность ионов меди в растворе электролита. (Здесь и далее активность определена для концентрации, выражаемой в моль/л). Анодный процесс – окисление и растворение цинка, его равновесный потенциал

, , (10.3)

где = –0,763 В; – активность ионов цинка. Суммарный потенциалобразующий процесс (реакция) в работающем элементе

,

а электродвижущая сила элемента Даниеля.

. (10.4)

Замечание. Для приблизительных расчетов ЭДС можно в уравнении (10.4) отношение активностей заменить отношением концентраций, моль/л

или , (10.5)

тогда

. (10.6)

Рассмотрим более сложный пример – марганцово-цинковый гальванический элемент (МЦЭ)

. (10.7)

В этом элементе анод – чистый металлический цинк, электрохимически растворяющийся при работе элемента

. (10.8)

Потенциал анодного процесса

. (10.9)

Катод в этом элементе представляет собой графитовый стержень (пластину), на который напрессована активная смесь оксида с графитом. Катодный процесс

, (10.10)

а электродный потенциал в предположении, что активности , и равны единице,

. (10.11)

Электродвижущая сила элемента

, (10.12)

то есть ЭДС зависит от концентрации ионов в электролите и рН электролита. Если теперь при определении суммарной потенциалобразующей реакции сложить анодную (10.8) и катодную (10.10) реакции, то получившееся уравнение

будет ошибочным. Это объясняется протеканием в элементе пяти вторичных процессов. Один из них

(10.13)

приводит к образованию на цинковом электроде труднорастворимой соли. «Освободившиеся» ионы с получающимися в катодном процессе ионами образуют слабый электролит

, (10.14)

который разлагается

. (10.15)

Марганцево-цинковый элемент – герметично замкнутая система, поэтому газообразный аммиак вступает в реакцию образования

. (10.16)

И, наконец, получающийся на катоде оксид образует кристаллогидрат

. (10.17)

Комбинирование реакций первичных (10.8) и (10.10) и вторичных (10.13–10.16) реакций позволяет определять суммарную реакцию уравнением

. (10.18)

В качестве примера вторичного ХИТ рассмотрим работу свинцового аккумулятора (изобретен в 1859 г., теория свинцового аккумулятора разработана в 1882 г.)

.

Процесс на левом электроде

(10.19)

протекает при работе (разряде) аккумулятора слева направо (анодный процесс) с образованием труднорастворимой соли , произведение растворимости которой , а при зарядке – справа налево (катодный процесс). Для работающего аккумулятора потенциал анода

(В). (10.20)

Процесс на правом электроде

(10.21)

протекает при работе аккумулятора слева направо (катодный процесс) и его потенциал

(В). (10.22)

При зарядке процесс (10.21) протекает справа налево (анодный процесс). Суммарный потенциалобразующая реакция в работающем свинцовом аккумуляторе

. (10.23)

ЭДС аккумулятора (В)

(10.24)

зависит от концентрации серной кислоты и уменьшается по мере работы из-за расхода кислоты.

Другими (кроме ЭДС) служебными характеристиками ХИТ являются:

– полное внутреннее сопротивление ;

– разрядное напряжение ;

– зарядное напряжение ;

– разрядная емкость – количество электричества, которое может быть получено от ХИТ

, в простейшем случае при ;

– расход активных веществ в расчете на 1 А·ч;

– коэффициент (доля) использования активных веществ;

– зарядная емкость , ;

– мощность – количество отдаваемой энергии в единицу времени;

– саморазряд – бесполезная потеря емкости при разомкнутой внешней цепи.

Снимаемое в реальных условиях эксплуатации напряжение разряда меньше определяемой по уравнению Нернста равновесной электродвижущей силы (см., например, уравнения 10.4, 10.12, 10.24) из-за поляризационных эффектов

.

Расход активных веществ при работе ХИТ рассчитывается по законам Фарадея. Для примера покажем расчет расхода активных веществ при работе свинцового аккумулятора. Уравнения анодного (10.19), катодного процесса (10.21) и суммарной потенциал-образующей реакции (10.23) записаны на два Фарадея электричества, поэтому расходы активных веществ на получение 1 А·ч электричества следует оценивать следующим образом.

Массы израсходованных свинца, его оксида и серной кислоты

;

;

.

Массы получающихся воды и труднорастворимой соли

;

.

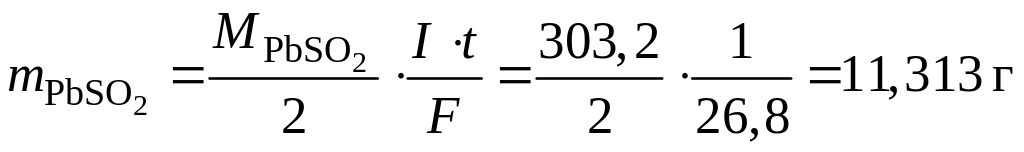При работе ХИТ выделяется или поглощается теплота, поэтому величины электродных потенциалов и ЭДС зависят от температуры. Эти зависимости определяют в виде ряда

, (10.25)

. (10.26)

Величины первого и второго термических коэффициентов приведены в справочниках. В приближенных расчетах величинами вторых коэффициентов пренебрегают и считают потенциалы и ЭДС линейными функциями температуры.

Влияние температуры на характеристики ХИТ можно оценить, если связать электродвижущую силу и изменение энергии Гиббса для потенциалобразующей (суммарной) химической реакции в ХИТ. Рассмотрим простой пример. Для гальванического элемента Даниэля

ЭДС определяется соотношением

. (10.27)

Возможность и направление протекания потенциалобразующей реакции этого гальванического элемента

определяется уравнением изотерм химической реакции

. (10.28)

Соотношения между ЭДС и термодинамическими характеристиками реакции определяются следующими уравнениями:

, (10.29)

, (10.30)

где – стандартное изменение энергии Гиббса; K – константа равновесия реакции; n – число электронов.

Так как ХИТ работают в узком температурном интервале, близком к стандартной температуре Т = 298 К, можно без большой ошибки считать

и .

С учетом известных термодинамических соотношений

можно получить такие уравнения

, (10.31)

, (10.32)

. (10.33)

В этих формулах – работа гальванического элемента, а – теплота, выделяющаяся или поглощающаяся при работе ХИТ. Если формулу (10.32) записать в виде

, (10.34)

то видно, что при химический источник тока превращает в полезную работу не только теплоту реакции, но и некоторое количество энергии, поглощаемое в виде теплоты из окружающей среды.