1. Теория электролитической диссоциации

Электролиты – твердые и жидкие вещества, молекулы которых в результате электростатического взаимодействия с молекулами полярного растворителя распадаются (диссоциируют) на ионы. Часто для краткости электролитами называют водные растворы кислот, оснований и солей, солевые и оксидные расплавы. Существование в растворах электролитов заряженных частиц определяет специфические свойства таких систем и, в первую очередь, их высокую электропроводность и протекание окислительно-восстановительных процессов на поверхности электродов, опущенных в раствор. С. Аррениус в 1884–87 гг. первым высказал предположение об увеличении числа частиц в растворе в результате диссоциации электролитов и на основании этого разработал элементарную теорию электролитической диссоциации, применимую для описания равновесий в растворах слабых электролитов.

Важнейшими характеристиками раствора электролита являются константа диссоциации и степень диссоциации. Степень диссоциации определяет долю молекул (молей) электролита, распавшихся на ионы, по отношению к числу молекул (молей) электролита, введенных в раствор. Степень диссоциации изменяется в пределах от =0 до =1. Плохо диссоциирующие электролиты <<1 называют слабыми. Для сильных электролитов 1. Константа диссоциации (константа равновесия процесса электролитической диссоциации) связана со степенью диссоциации.

Например, для водных растворов бинарных одно-однозарядных (HCl, HNO₃, CH₃COOH, NaCl и др.) и двух-двухзарядных электролитов (ZnSO₄, CuS, AlPO₄ и др.) для процесса диссоциации

константы диссоциации определяются уравнениями

(1.1)

В этих уравнениях , , и т.д. – равновесные концентрации ионов и непродиссоциировавших молекул электролитов, моль/л; – концентрация введенных в воду молекул электролита («начальная» концентрация, концентрация «по приготовлению», концентрация «до диссоциации»), моль/л. Для сильных электролитов константа диссоциации большая величина и степень диссоциации близка к единице (например, при 25 С K_д(HCl)=10⁷, 1; K_д(HNO₃)=37, =0,995 при =0,3 моль/л). Для слабых электролитов константа диссоциации мала, а степень диссоциации составляет несколько процентов (например, для уксусной кислоты CH₃COOH K_д=1,8510^–5, =0,013 или 1,3% для =0,1 моль/л). Поэтому для слабых электролитов при приближенных расчетах в уравнении (1.1) в знаменателе пренебрегают слагаемым  по сравнению с единицей

(1.2)

Однако, для сильно разбавленных растворов и слабых электролитов степень диссоциации близка к единице , поэтому уравнение (1.2) становится неверным.

Для тройных электролитов уравнение, связывающее константу диссоциации со степенью диссоциации, имеет другой вид. Например, для сильного электролита

. (1.3)

Для слабого электролита

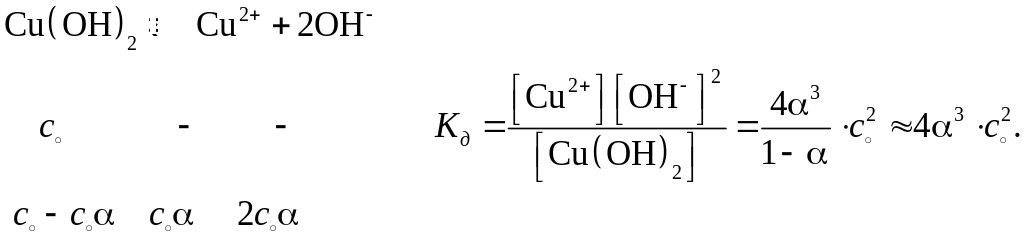(1.4)

Для более сложных электролитов

(1.5)

(1.6)

Замечания.

1. Записанные выше уравнения процессов диссоциации, строго говоря, следует понимать не как равновесие между ионами и непродиссоциировавшими молекулами электролита, а как равновесие между обособленными гидратированными ионами, относительно независимо перемещающимися в растворе, и ионами, образующими пары.

2. Сложные электролиты в водных растворах диссоциируют ступенчато, например:

а)

суммарный процесс получается сложением ступенчатых

б)

суммарный процесс

Это обстоятельство следует учитывать при точных расчетах, а экспериментально определенную степень диссоциации следует считать кажущейся.

3. Увеличение числа частиц при диссоциации определяется степенью диссоциации:

Число i, определяющее во сколько раз увеличивается число частиц, называется изотоническим коэффициентом Вант-Гоффа. В общем случае

(1.7)

где  – число ионов, получающихся при диссоциации молекулы электролита.

С учетом диссоциации известные закономерности, справедливые для растворов неэлектролитов, должны быть скорректированы:

– закон Рауля

(1.8)

– эбулиоскопический эффект

(1.9)

– криоскопический эффект

(1.10)

– осмотическое давление

(1.11)

Здесь все формулы написаны для бинарного раствора; n₁, n₂ – числа молей компонентов; p₁ – давление паров растворителя; – повышение температуры кипения раствора электролита; _m – понижение температуры замерзания раствора; E, K – эбуллиоскопическая и криоскопическая постоянные растворителя; с₂, с_m2 – молярная и моляльная концентрации электролита.