Уравнение изотермы адсорбции Гиббса
В теории Гиббса адсорбцией называется самопроизвольное изменение концентрации компонентов системы в поверхностном слое по сравнению с концентрацией в объёмах фаз.
Адсорбционная способность веществ оценивается удельной адсорбцией Гi , которая определяется соотношением:
Гi = Nis / S, [моль /м2]. (14)
Nis - избыток i - компонента в поверхностном слое с площадью
S = 1.
Фундаментальное уравнение, описывающее адсорбцию при Т = const, через химический потенциал (μ) имеет следующий вид:
dσ + Σ Гi dμi = 0. (15)
Для двухкомпонентных растворов уравнение (15) преобразуется в следующее:
dσ + Г1μ1 + Г2μ2 = 0. (16)
где Г1 ,μ1 - величины, характеризующие первый компонент (растворитель); Г2 ,μ2 - величины, характеризующие второй компонент (растворённое вещество).
В уравнении (16) σ определяется экспериментально, Гi в этом уравнении однозначно не определить, примем, что разделяющая поверхность фиксируется в таком положении, чтобы Г1 = 0. Тогда уравнение (16) примет вид:
Г2 = - dσ / dμ2. (17)
Подставим dμ = RT (da/a) в уравнение (17) получим уравнение Гиббса.
Индекс «2» опущен, так под Г понимается удельная адсорбция растворённого вещества.
а dσ
Г = - ---- ----.
R∙T da (18)
Для разбавленных растворов активность коэффициент активности
γ ± = 1 (активность а ± = γ ± ∙С). С – концентрация раствора.
С dσ
Г = - ---- ----.
R∙T dС (19)
Здесь: Г – удельная адсорбция; σ – поверхностное натяжение раствора с концентрацией С; R - газовая постоянная (Дж/моль К); Т – температура в К.
Знак и величина удельной адсорбции растворённого вещества определяется производной dσ/ dС .
Из (19) видно, что Г>0 при dσ/ dС < 0. Концентрация растворённого вещества в поверхностном слое больше, чем в объёме. То есть при добавлении этого вещества в раствор поверхностное натяжение снижается.
Эти вещества, менее полярные, чем растворитель (обычно это вода), понижают поверхностное натяжение, Они адсорбируются положительно.
При добавлении веществ, более полярных, чем растворитель поверхностное натяжение увеличивается dσ/ dС > 0 и Г<0. Эти вещества называют поверхностно-инактивными, их концентрация в поверхностном слое меньше, чем в объём. Это соли, их ионы притягивают ионы воды с большей силой, чем молекулы воды друг к другу.
Вещества, способные изменять поверхностное натяжение жидкостей, называются поверхностно – активными (ПАВ). Это вещества, молекулы которых содержат полярную группу (NO2- , -NH2 ,- ОН, - СООН, -О - , - SO2 OH) и неполярный радикал. Такие молекулы называются дифильными
и изображаются символом ○─────, в котором кружочком обозначается полярная часть молекулы, а прямая или волнистая линия - неполярная часть. Если в данном растворителе полярная часть диссоциирует, то поверхностно – активное вещество называют ионогенным, в противном случае – неионогенным. Например, спирты или органические кислоты: СН3 - (СН2)n - ОН; СН3 - (СН2)n - СООН.
Полярные группы обладают большим сродством к полярным жидкостям, в частности к воде, они лиофильны (гидрофильны). Углеводородные радикалы неполярные, они лиофобны (по отношению к воде - гидрофобны).
Учитывая уравнение (19), можно определить удельную адсорбцию. Построят зависимость σ = f(С), по графику находят dσ/ dС - тангенс угла наклона в данной точке, либо определяют произведение С ∙ (dσ/d С), оно равно отрезку АВ на оси ординат. См. рис. 21а. и рис. 21б.
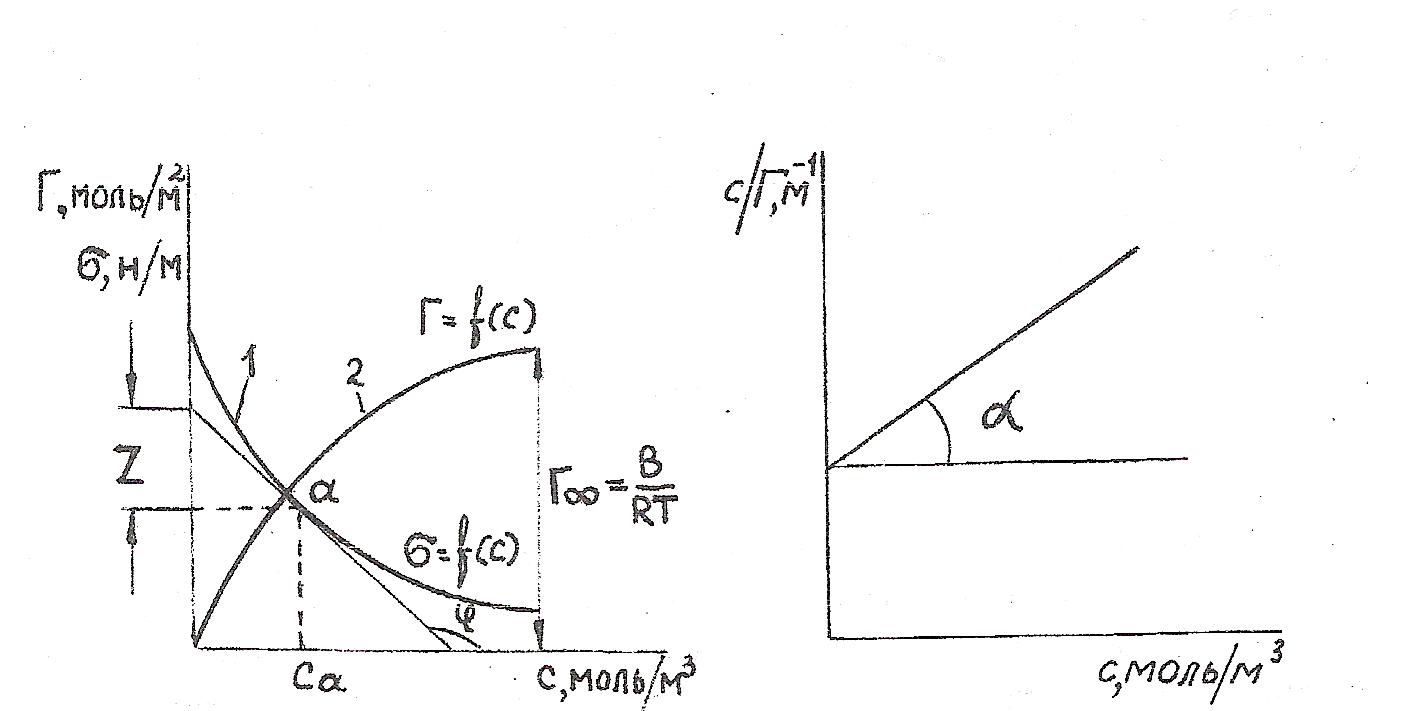
а. б.
Рис. 21а. Зависимость поверхностного натяжения (кривая 1) и удельной адсорбции от концентрации ПАВ (кривая 2).
Рис. 21б. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра.
Б. А. Шишковский в эмпирическом уравнении показал, что поверхностное натяжение снижается с возрастанием концентрации ПАВ.
Δ = σ0 - σ = σ0 ∙В ∙(С/А + 1), (20)
где А и Б – эмпирические константы.
Дифференцируя это уравнение, получаем:
-dσ/dС =В∙σ0/ (А +С). (21)
Подставим (21) в (19).
В ∙σ0 С/А
Г = ---- ---------- .
R∙T 1 + С/А
Обозначим В∙σ0 / RT через Г∞ - предельная адсорбции при высоких концентрациях, а 1/А через к, получим:
Г = Г∞ ∙ к ∙ С / (1 + к ∙С). (22)
Таким образом, получается уравнение Ленгмюра. Из него становится понятен смысл констант (А и В) в уравнении (20).При высоких концентрациях раствора, когда С>> A В∙σ0 / R∙T= Г∞ , В = Г∞ ∙R∙T/ σ0, т. е. постоянное предельное значение для каждого гомологического ряда (рис. 22).
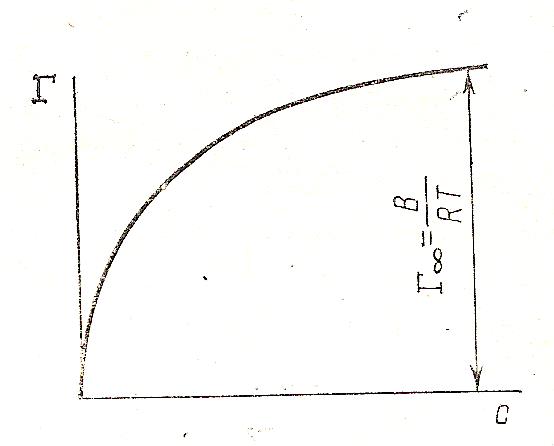
Рис. 22. Изотерма адсорбции по уравнению 22.
Тогда константа А – адсорбционная способность вещества при малых концентрациях.
Уравнение (22) было получено для адсорбции газов на твёрдых телах. Для адсорбции на границе раствор – газ им был сформулирован принцип независимости поверхностного действия Ленгмюра (1915г.).
Для своей теории он сформулировал допущения.
1. Адсорбция локализована (молекулы не перемещаются по поверхности).
2. Поверхность эквипотенциальна, т.е. во всех точках одинаковое поверхностное натяжение.
3. Адсорбируемые молекулы не взаимодействуют между собой.
Эти принципы он перенёс к поверхности раздела фаз газ- жидкость.
Он предположил, что при адсорбции ПАВ полярные группы, обладающие большим сродством к полярной фазе, например, к воде, они втягиваются в воду. В то время как, неполярная группа (радикал) выталкивается в неполярную среду (воздух). При этом происходит уменьшение свободной энергии, площадь раздела фаз увеличивается, ограничивая размеры поверхностного слоя толщиной в одну молекул. При малых концентрациях ПАВ углеводородные цепи «плавают» на поверхности, а полярная группа погружена в воду.
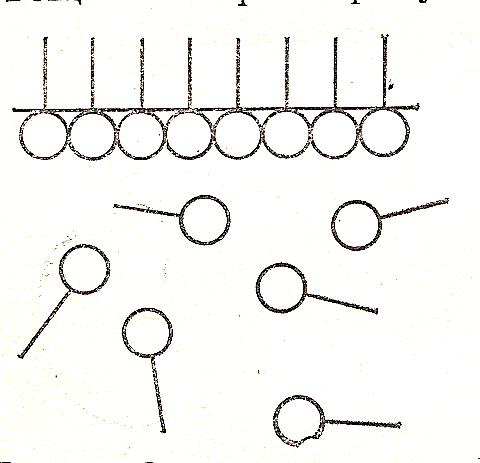
Рис.23. Схема мономолекулярного слоя при Г = Г∞ .
Такое положение возможно из-за гибкости углеводородной цепи. С ростом концентрации, число молекул в поверхностном слое увеличивается, цепи поднимаются вертикальное положение. Значение поверхностного натяжения уменьшается, приближаясь к его значению ПАВ в его чистом растворе.
Образуется мономолекулярный слой, так называемый «мономолекулярный частокол» (рис 23). На поверхности раздела может адсорбироваться один слой молекул с плотной «упаковкой», поэтому значение удельной адсорбции Г отвечает её предельной величине - Г∞ (за счёт образования на поверхности насыщенного монослоя ПАВ). Эта теория в дальнейшем была подтверждена рентгенографией. По величине предельной адсорбции Г∞ можно определить размеры ПАВ: площадь поперечного сечения
So = 1/ Г∞ ∙Na. (23)
и длину молекулы
δ = Г∞ ∙М / ρ. (24)
Здесь Na = 6, 02205 1023 моль-1 (постоянная Авогадро), М и ρ –молекулярная масса и плотность ПАВ.
Правило Дюкло – Траубе.
Было обнаружено, что каждый последующий член гомологического ряда
сильнее понижает поверхностное натяжение, чем предыдущий (при С→0).
. ( dσ/dC)k+1 /( dσ/dC)k = Gk+1 /Gk = a, (25)
где (- dσ/dC) С→0 = G поверхностная активность вещества; число атомов углерода в неполярной молекуле ПАВ; а – константа для каждого гомологического ряда ( обычно от 3, 0 до 3,5). Рис.24.
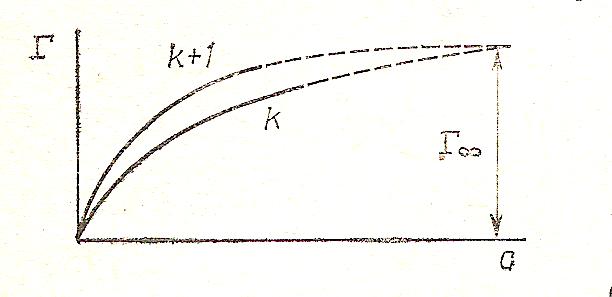
Рис. 24. Изотермы адсорбции ПАВ одного гомологического ряда на поверхности растворов.
Причина заключается в том, что с увеличением длины углеводородной цепи уменьшается растворимость, и тем самым увеличивается стремление молекул вещества перейти из объёма в поверхностный слой.
Из соотношения (19) и (25) видно, что при Сk+1 = Сk
Gk+1 /Gk = Гr+1 /Гk , т.е. удельная адсорбция последующего члена гомологического ряда больше, чем предыдущего. При высоких концентрациях удельная адсорбция всех членов гомологического ряда стремится к предельному значению. Это подтверждается постоянство константы
В = Г∞ ∙RT/ σ0, т.е. при высоких концентрациях в растворе образуется насыщенный монослой. При такой ориентации удельная адсорбция определяется площадью поперечного сечения молекулы ПАВ, одинаковой доя каждого члена гомологического ряда. Исследования показали, что константа «а» увеличивается с ростом k.