2.4. Время полупревращения или полураспада

Для характеристики реакций часто пользуются временем полупревращения или полураспада t_1/2, равным промежутку времени, в течение которого реагирует половина взятого количества вещества. Особенно это важно для реакций первого порядка, к которым принадлежат реакции радиоактивного распада.

Для реакции I порядка, при С = 0,5 С₀ подстановкой в уравнение получаем (10):

Т.е. время полупревращения не зависит от количества или концентрации исходного вещества и обратно пропорционально константе скорости реакции.

Для реакции второго порядка C = С₀ – С = 0,5 С_0, подставим в уравнение

(16):

12

В данном случае время полупревращения обратно пропорционально начальной концентрации исходного вещества.

Для реакции третьего порядка С = С₀ – С = 0,5 С₀, подставляем в уравнение

(19):

Здесь время полупревращения обратно пропорционально квадрату начальной концентрации исходных веществ (при условии равенства исходных концентраций веществ А₁ и А₂ и А₃).

2.5. Способы определения порядка реакции для элементарных и формально простых реакций в закрытых системах

Рассмотрим простую реакцию n₁-го порядка по А₁ и n₂ по А₂:

Порядок реакции определяют, используя только опытные данные изменения концентрации реагирующих веществ со временем.

Зависимость скорости реакции от концентрации вычисляется по уравнению:

Общий порядок равен:

где n₁– порядок по А₁ и n₂ – по А₂, k – константа скорости реакции.

Если реакция (23) элементарная, то порядок реакции совпадает со стехиометрическими коэффициентами (а = а₁ + а₂).

Для того, чтобы скорость реакции зависела только от одного исходного вещества, используют метод избыточных концентраций.

Метод избыточных концентраций (или метод Оствальда)

13

Проводят серию опытов, в каждом из которых изучается влияние концентрации только одного из исходных веществ на скорость реакции. Для этого все остальные исходные вещества, берутся в

таком избытке по сравнению с исследуемым веществом, чтобы их концентрация была практически постоянной.

При протекании реакции считаем, что меняется только концентрация А₁, а концентрация А₂ остается постоянной, тогда:

где:

Затем берем избыток А₁ по сравнению с А₂ и получаем:

где:

Затем определяем порядок реакции по одному из ниже описанных методов.

Способы расчета порядка по данному веществу разделяются на дифференциальные и интегральные.

Дифференциальный способ.

На опыте получают зависимость концентрации вещества от времени. Скорость реакции определяют при помощи графического дифференцирования (путем проведения касательных в разных точках кинетической кривой). Т.е. находят тангенс угла этой касательной – это производная концентрации по времени (скорость образования данного вещества в данный момент времени).

1. Способ логарифмирования.

Прологарифмируем уравнение:

получим:

14

Тогда отрезок на оси ординат даст значение lnk, а тангенс угла наклона прямой – это порядок n₁ реакции по веществу А₁.

Аналогично проводят расчет с веществом А₂, тогда общий суммарный порядок n = n₁ + n₂.

Основной недостаток метода – большая погрешность при определении тангенса угла наклона, достоинство – простота расчета.

Интегральные способы.

В этих способах используют выражения для зависимости концентрации вещества от времени, получаемые опытным путем или после интегрирования уравнений:

или

1. Способ подстановки.

Интегрируем уравнения (8), (14), (18) в пределах от 0 до t и от С₀ до С

при n = 1, 2, 3

получаем:

при n = 1

при n = 2

при n = 3

где С₀ – начальная концентрация.

Подставляя в эти уравнения значение концентраций исследуемого вещества в разные моменты времени, вычисляем k. Порядок реакции будет соответствовать тому уравнению, где значение k останутся постоянными.

15

Рассчитывая порядок по данному исходному веществу, перечисленными ниже способами, определяем определяем общий порядок реакции, а затем константу скорости реакции

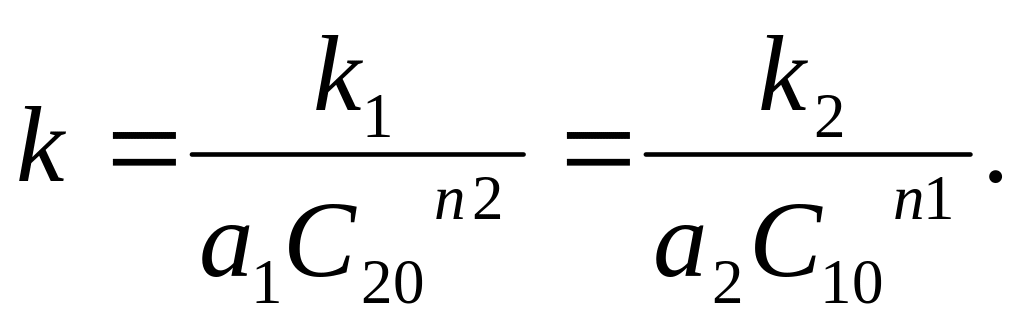
2. Графический метод.

Ниже приведены дифференциальные уравнения скоростей реакций различных порядков и их решения.

Порядок Уравнение скорости Решение уравнения

реакции

n = 1

n = 2

n = 3

Отложив на оси абцисс время t, а на оси ординат lnC, 1/С и 1/С² для изучаемой реакции получают зависимости, и та из них, которая соответствует порядку данной реакции, будет прямой.

3.Определение времени полупревращения.

Подставляя в уравнение (20), (21) и (22)

С = 0,5 С₀, получаем:

при n = 1

при n = 2

16

при n = 3

Проводим несколько опытов при разных начальных концентрациях. Как видно, при n = 1 время полупревращения не

зависит от C₀; при n = 2 – обратно пропорционально С₀; а при n = 3 – обратно пропорционально квадрату С₀.

По характеру этих зависимостей делаем вывод о порядке реакции.

4. Способ Вант - Гоффа.

Если порядок нецелочисленный, то общее уравнение для t_1/2:

Логарифмируя это уравнение, получим:

,

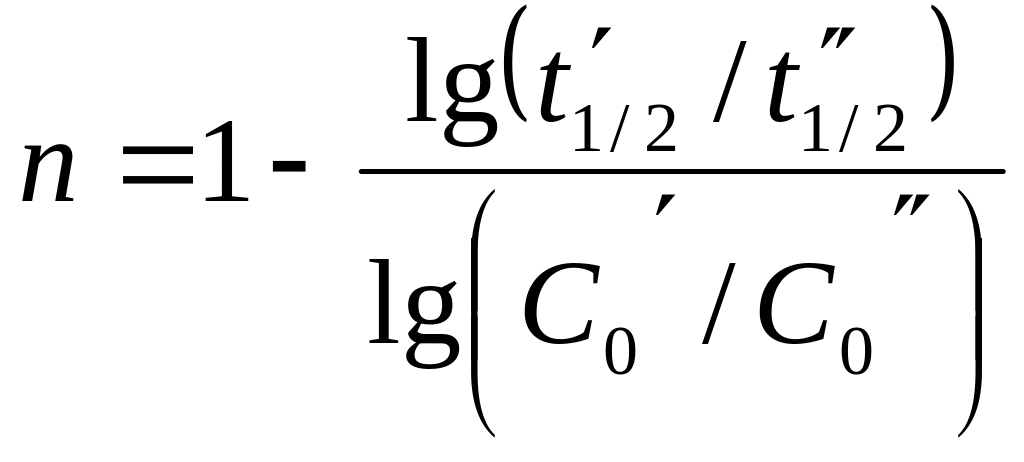где C'₀ и C"₀ – два значения концентраций компонентов соответствующих t'_1/2 и t"_1/2.