9. Транспортная задача

Транспортная задача возникает при формализации множества различных прикладных задач. Здесь будет рассмотрена одна из наиболее простых прикладных задач. Пусть в m пунктах (складах) у поставщиков имеется однородный груз в количестве a₁, a₂,…,a_m единиц соответственно. Имеющийся груз необходимо доставить n потребителям, чьи потребности в грузе соответственно равны b₁, b₂,…,b_n. Известны стоимости c_ij перевозки одной единицы груза от i –го поставщика j –му потребителю. Требуется составить план перевозок, при котором у поставщиков будет вывезен весь груз, а потребителям доставлено ровно столько, сколько нужно. При этом требуется, чтобы суммарная стоимость перевозок была минимальной.

Обозначим x_ij – количество единиц груза, перевозимого от i –го поставщика j –му потребителю, i =1,…,m, j =1,…,n. Естественно предположить, что x_ij ≥0 (Груз везут от поставщиков потребителям, а не наоборот). Обозначим

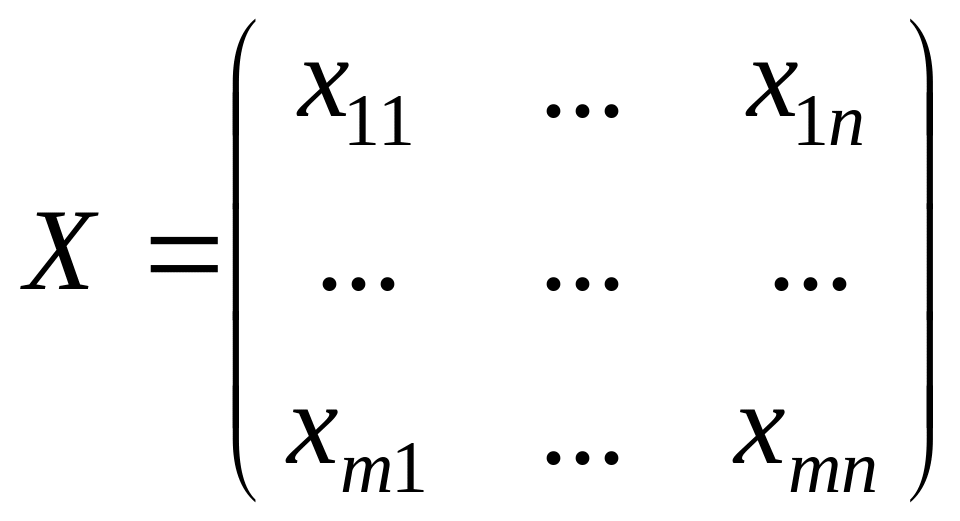
Матрицу перевозок. Тогда транспортная задача формализуется следующим образом

∑_i∑_j x_ijc_ij →min

x₁₁ +…+ x_1n = a₁ ,

……………….

x_m1 +…+ x_mn = a_m , (1.17)

x₁₁ +…+ x_m1 = b₁ ,

…………………

x_1n +…+ x_mn = b_n ,

x_ij ≥0 .

Теорема 1.9.1 (о существовании решения)

Для того, чтобы транспортная задача имела решение (оптимальный план) необходимо и достаточно выполнения равенства

a₁ +…+ a_m = b₁ +…+ b_n (1.18)

Определение 1.9.1. Транспортная задача называется закрытой, если выполняется равенство (1.18), в противном случае она называется открытой.

Ограничение на то, чтобы транспортная задача была закрытой, требуется для работы рассматриваемого далее алгоритма по ее решению и на практике может быть легко обойдено. Пусть не выполняется равенство (1.18). Для определенности рассмотрим случай

a₁ +…+ a_m > b₁ +…+ b_n .

Тогда нужно ввести фиктивного n + 1 потребителя с потребностью

b_n+1 = a₁ +…+ a_m – (b₁ +…+ b_n).

Фиктивного потребителя нет в реальности, следовательно, никто ему груз не повезет. Поэтому стоимость перевозок фиктивному потребителю полагаем равной нулю c_in+1 =0, i = 1,…,m. Далее решается закрытая задача, а груз, поставляемый по оптимальному плану, фиктивному потребителю останется на складе у соответствующего поставщика.

Аналогично, в случае неравенства

a₁ +…+ a_m < b₁ +…+ b_n

вводится фиктивный m + 1 поставщик, с запасом на складе в объеме

a_m+1 = b₁ +…+ b_n – ( a₁ +…+ a_m ).

Стоимость перевозки единицы груза от фиктивного поставщика любому потребителю будет равна нулю c_m+1j =0, j = 1,…,n. Затем решается закрытая задача, а груз, который поставил фиктивный поставщик, соответствующий потребитель не дополучит. Транспортная задача является частным случаем задачи линейного программирования. Для нее разработан специальный алгоритм решения. Общая схема решения закрытой транспортной задачи выглядит следующим образом:

- находится начальный опорный план;

- план проверяется на оптимальность;

- если план оптимальный, то алгоритм работу закончил, если план не оптимальный, то нужно перейти к новому, более «хорошему» (т.е. меньшей стоимости) плану;

- новый план проверяется на оптимальность и т. д.

Построение начального опорного плана методом минимального элемента.

Запишем таблицу

	b1	b2	…	bn
a1	c11	c12	…	c1n
a2	c21	c22	…	c2n
…	….	…	…	…
am	cm1	cm2	…	cmn

Выберем среди клеток со стоимостями c_ij клетку с минимально стоимостью и заполняем ее максимальной допустимой поставкой. Вычитаем из соответствующих запасов поставщика и требуемой величины поставки у потребителя, найденную величину поставки. Если у поставщика после вычитания не осталось груза на складе, то все клетки соответствующей строки далее не рассматриваются. Если потребителю после найденной поставки доставлен весь требуемый груз, то все клетки соответствующего столбца далее не рассматриваются. Операция повторяется, пока остается не распределенный груз.

Определение 1.9.2. Будем говорить, что клетка является занятой, если в нее распределена некоторая поставка. В противном случае, клетка называется свободной.

Будем говорить, что занятые клетки образуют цикл, если можно, начиная из некоторой занятой клетки, чередуя шаги по вертикали и горизонтали, шагая только по занятым клеткам вернуться в исходную клетку. При этом можно перешагивать через любое количество занятых и незанятых клеток. Клетки, через которые перешагнули, в цикле не участвуют. Нельзя шагать в клетки, куда уже был сделан один из предыдущих шагов. В каждой строке и в каждом столбце должно быть не более двух клеток, участвующих в цикле.

Составленный по методу минимального элемента начальный план является опорным, т. е. в этом плане не более чем m + n – 1 занятая клетка. Кроме того, занятые клетки не образуют циклов.

Пример. Пусть задана транспортная задача: a₁ = 50, a₂ = 70, a₃ = 90, b₁ = 50, b₂ = 40, b₃ = 70, b₄ = 40, а матрица стоимостей имеет вид

	b1 = 50	b2 = 40	b3 = 70	b4 = 40
a1 = 50	8	11	10	13
a2 = 70	10	10	12	14
a3 = 90	11	9	10	12

Так как a₁ + a₂ + a₃ =210> b₁ + b₂ + b₃ + b₄ =200, то задача не закрытая. Для выполнения равенства вводим фиктивного потребителя с объемом потребности b₅ = 10, а стоимости перевозок этому потребителю положим равными нулю. Получили матрицу

	b1 = 50	b2 = 40	b3 = 70	b4 = 40	b5 = 10
a1 = 50	8	11	10	13	0
a2 = 70	10	10	12	14	0
a3 = 90	11	9	10	12	0

Построим начальный опорный план по методу минимального элемента. В первую очередь нас интересуют клетки соответствующие реальным поставщикам. Среди них (1;1) - клетка с минимальной стоимостью (8 единиц). Этой клетке соответствует потребность в 50 единиц груза, а у поставщика имеется 50 единиц груза. Значит, можем сделать в эту клетку поставку величиной min{50; 50} =50. Заполняем эту поставку. Новые потребности потребителей и возможности поставщиков указаны в скобках.

	b1 = 50(=0)	b2 = 40(=0)	b3 = 70	b4 = 40	b5 = 10
a1 = 50 (=0)	8 50	11	10	13	0
a2 = 70	10	10	12	14	0
a3 =90	11	9	10	12	0

Так как первому потребителю доставлен весь необходимый груз, то клетки (2;1), (3;1) в дальнейшем поиске минимума не участвуют. У первого поставщика вывезен весь груз, поэтому клетки (1;2), (1;3), (1;4), (1;5) в дальнейшем поиске минимума не участвуют. Из оставшихся клеток реальных поставщиков и реальных потребителей минимальную стоимость имеет клетка (3;2) (9 единиц). В клетке (3;2) величина поставки будет min{90; 40}=40 Делаем поставку в клетку (3;2) величиной 40. Таблица приобретает вид

	b1 = 50(=0)	b2 = 40(=0)	b3 = 70	b4 = 40	b5 = 10
a1 = 50 (=0)	8 50	11	10	13	0
a2 = 70	10	10	12	14	0
a3 =90 (=50)	11	9 40	10	12	0

Так как второму поставщику поставлено груза в объеме его потребности, то клетка (2;2) в дальнейшем поиске минимума не участвует (клетка (2;1) выбыла раньше). Из оставшихся реальных клеток минимальную стоимость имеет клетка (3;3) (10 единиц). Величина поставки в эту клетку равна min{50; 70}=50. Вписываем эту поставку.

	b1 = 50(=0)	b2 = 40(=0)	b3 = 70(20)	b4 = 40	b5 = 10
a1 = 50 (=0)	8 50	11	10	13	0
a2 = 70	10	10	12	14	0
a3 =90 (=50)(0)	11	9 40	10 50	12	0

Так как у третьего поставщика вывезен весь груз, клетки (3;4) и (3;5) в дальнейшем поиске минимума не участвуют. Из оставшихся реальных клеток минимальную стоимость имеет клетка (2;3) (12 единиц). Величина поставки в эту клетку равна min{70; 20}=20. Вписываем эту поставку.

	b1 = 50(=0)	b2 = 40(=0)	b3 = 70(20)	b4 = 40	b5 = 10
a1 = 50 (=0)	8 50	11	10	13	0
a2 = 70 (50)	10	10	12 20	14	0
a3 =90 (=50)(0)	11	9 40	10 50	12	0

Остались только две клетки (2;4) (2;5) в которые можно сделать поставки соответственно min{50; 40}=40 и 10. Записываем эти поставки.

	b1 = 50(=0)	b2 = 40(=0)	b3 = 70(20)	b4 = 40(0)	b5 = 10(0)
a1 = 50 (=0)	8 50	11	10	13	0
a2 = 70 (50)(10)(0)	10	10	12 20	14 40	0 10
a3 =90 (=50)(0)	11	9 40	10 50	12	0

Начальный опорный план по методу минимального элемента составлен. Занятыми являются клетки: (1;1), (2;3), (2;4), (2;5), (3;2), (3;3). Всего занятых клеток 6 < 7=3+5-1.

Определение 1.9.3. Опорный план, в котором ровно m +n – 1 занятая клетка называется невырожденным. В случае, когда занятых клеток меньше величины m +n – 1, опорный план называется вырожденным.

В нашем примере начальный опорный план получился вырожденным. Для дальнейших действий по проверке плана на оптимальность будем применять метод потенциалов. Для работы по методу потенциалов необходимо, чтобы опорный план был не вырожденным. Чтобы опорный план в нашем примере стал невырожденным нужно занять еще одну клетку. Так как весь груз уже распределен, займем эту клетку нулевой (фиктивной) поставкой. Нужно занять такую клетку, чтобы занятые клетки не образовывали циклов. В нашем примере клетку (3; 5) занимать нельзя, так как образуется цикл (3; 5), (2; 5). (2; 3), (3; 3), (3; 5). Можно занять клетку (2;1), в этом случае цикл не образуются. Теперь матрица имеет вид

	b1 = 50(=0)	b2 = 40(=0)	b3 = 70(20)	b4 = 40(0)	b5 = 10(0)
a1 = 50 (=0)	8 50	11	10	13	0
a2 = 70 (50)(10)(0)	10 0	10	12 20	14 40	0 10
a3 =90 (=50)(0)	11	9 40	10 50	12	0

Составление начального опорного плана закончено. Все действия по составлению начального опорного плана, в целях экономии времени, можно проводить на одной матрице.

Перейдем к проверке плана на оптимальность. Для этой проверки используем следующую теорему.

Теорема 1.9.2. (Признак оптимальности)

Если план транспортной задачи является оптимальным, то ему соответствует система из m + n чисел , удовлетворяющих условиям:

- для занятых клеток ;

- для свободных клеток .

Числа и называются потенциалами соответственно i- го поставщика и j- го потребителя. Если рассматривать транспортную задачу как задачу линейного программирования, то эти числа являются двойственными оценками исходной задачи (1.17). Величина показывает величину увеличения (если ) или уменьшения (если ) значение целевой функции транспортной задачи, если в клетку (i; j) сделать поставку равную 1.

Проверка плана на оптимальность проводится следующим образом. Решается система уравнений

(1.19)

Так как уравнений m +n – 1 (по количеству занятых клеток), то решений бесконечно много. Выделяем одно из них, полагая один из потенциалов равным нулю. Нулем лучше положить потенциал, которому соответствует наибольшее количество занятых клеток. После того, как все потенциалы найдены, проверяем выполнение оценок

(1.20)

для всех свободных клеток. Если все неравенства (1.20) выполняются, то план оптимальный. Пусть имеется несколько отрицательных оценок (1.20). Тогда переходим к построению нового опорного плана.

Выбираем наибольшую по модулю отрицательную оценку. Напомним, что отрицательная оценка показывает, на какую величину убудет целевая функция, если в эту клетку сделать поставку в единицу груза. Следовательно, так как требуется минимизировать целевую функцию, выгодно сделать в эту клетку наибольшую возможную поставку. Чтобы определить величину поставки и те клетки, в которых будут изменяться величины поставок, строим, начиная из выбранной клетки, цикл по занятым клеткам. Такой цикл существует и притом только один. Выбранную клетку помечаем знаком «+», а далее по циклу чередуем знаки. Затем среди клеток помеченных знаком «–» выбираем наименьшую поставку d. Далее, двигаясь по циклу, прибавляем величину d в клетках помеченных знаком «+» и вычитаем величину d в клетках помеченных знаком «–». Получен новый опорный план. Затем нужно снова проверить его на оптимальность и т.д., пока не будет найден оптимальный план.

Запишем в нашем примере уравнения для занятых клеток.

.

Положим тогда, решая эти уравнения, получим

.

Теперь вычислим оценки для свободных клеток по формуле (1.20).

, , , ,

, , , .

Имеется клетка с отрицательной оценкой, значит план не оптимальный. Так как только одна клетка (2; 2) имеет отрицательную оценку, то будем заполнять поставкой именно эту клетку. Строим цикл, начиная из клетки (2; 2). Получается следующий цикл

(2; 2), (2; 3), (3:3), (3; 2), (2; 2).

При этом, знаком «+» помечены клетки (2; 2), (3:3), а знаком «–» клетки (2; 3), (3; 2).

	v1 = 10	v2 = 11	v3 = 12	v4 = 14	v5 = 0
u1 = – 2	8 50	11	10	13	0
u2 = 0	10 0	+ 10	– 12 20	14 40	0 10
u3 = – 2	11	– 9 40	+ 10 50	12	0

Среди клеток, помеченных знаком «–» минимальная поставка равна 20. В клетках помеченных знаком «–» вычтем эту величину, а в клетках помеченных знаком «+» добавим эту величину. Получим матрицу с новым опорным планом. Рассчитаем для него потенциалы.

	v1 = 10	v2 = 10	v3 = 9	v4 = 14	v5 = 0
u1 = – 2	8 50	11	10	13	0
u2 = 0	10 0	10 20	12	14 40	0 10
u3 = – 1	11	9 20	10 70	12	0

Рассчитаем оценки свободных клеток

, , , , , , , .

План снова не оптимальный. Нужно сделать максимально возможную поставку в единственную клетку с отрицательной оценкой (3; 4). Находим цикл, начиная из этой клетки. Это будет цикл (3; 4), (3; 2), (2; 2), (2; 4), (3; 4). Расставляем знаки

	v1 = 10	v2 = 10	v3 = 9	v4 = 14	v5 = 0
u1 = – 2	8 50	11	10	13	0
u2 = 0	10 0	+ 10 20	12	– 14 40	0 10
u3 = – 1	11	– 9 20	10 70	+ 12	0

Среди клеток, помеченных знаком «–» минимальная поставка – 20. Так же как в прошлый раз, прибавляем и вычитаем эту величину из поставок в помеченных клетках в соответствии со знаком. Рассчитываем вновь потенциалы.

	v1 = 10	v2 = 10	v3 = 8	v4 = 14	v5 = 0
u1 = – 2	8 50	11	10	13	0
u2 = 0	10 0	10 40	12	14 20	0 10
u3 = – 2	11	9	10 70	12 20	0

Тогда оценки свободных клеток будут иметь вид

, , , , , , , .

Так как все оценки не отрицательные, то план оптимальный. Запишем ответ:

- первый поставщик везет первому потребителю 50 единиц груза;

- второй поставщик везет второму потребителю 40 единиц груза, четвертому потребителю 20 единиц и 10 единиц груза у него остается на складе (пятого потребителя не существует);

- третий поставщик везет третьему потребителю 70 единиц груза, а четвертому потребителю – 20.

Литература

1. Акулич И.Л. Математическое программирование в примерах и задачах: Учебное пособие.2-е изд. – СПб [и др.]: Лань, 2009. – 352с.

2. Кузнецов А.В. Высшая математика: математическое программирование: учебник/Кузнецов А.В., Сакович В.А., Холод Н.И.; Кузнецов А.В. (общ. ред.). – СПб [и др.]: Лань, 2010. – 351с.

3. Таха Х. Введение в исследование операций, 7-е издание. Пер. с англ.- М.: Издательский дом «Вильямс», 2005.- 912с.

4. Шапкин А.С., Мазаева Н.П. Математические методы и модели исследования операций: Учебник. – М.: Издательско-торговая корпорация «Дашков и К◦», 2004. – 400с.

5. Элементы линейного программирования: Методические указания/ Рольщиков В.Е. – Челябинск: Челябинский государственный университет, 2000. 50с.

6. Введение в сетевые методы: Методические указания/ Рольщиков В.Е. – Челябинск: Челябинский государственный университет, 2000. 21с.

1. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. М.: Высш. шк., 1986. 287с.

2. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. М.: Высш.шк., 1979. 124с.

3. *Костевич Л.С., Лапко А.А. Теория игр. Исследование операций. Минск: Вышейш. шк., 2008. – 368с.