Учебное пособие по дисциплине

«Методы оптимальных решений»

Введение

В данном пособии рассматриваются методы оптимизации, применяемые для решения задач, возникающих в математических моделях экономики. Будут рассмотрены методы решения задач линейного программирования, транспортная задача, задачи на потоки в сетях, задачи о распределении инвестиций, задача «коммивояжера», задача о загрузке, задача о замене оборудования, некоторые задачи управления запасами. Пособие предназначено для студентов заочного отделения экономического факультета.

1. Линейные задачи оптимизации

Многие задачи в экономике являются многовариантными. Среди множества возможных вариантов решения приходится отыскивать наилучшее в некотором смысле. При этом решение должно удовлетворять ограничениям, определяемым природными, экономическими и технологическими возможностями. Пусть различные варианты решения получаются за счет выбора вектора x=(x₁,…, x_n) управляющих параметров из множества X. Если критерием, по которому отбирается лучшее решение, является линейная по переменным x₁,…, x_n функция (целевая функция), а множество X задается системой линейных по тем же переменным уравнений и неравенств, то такая задача называется задачей линейного программирования.

Одним из основоположников теории линейного программирования был Л.В. Канторович. В 1939 году вышла его работа «Математические методы организации и планирования производства». Спустя 10 лет американский математик Дж. Данциг разработал эффективный метод решения данного класса задач – симплекс-метод.

Итак, линейное программирование – раздел математики, в котором разработаны методы нахождения экстремума (минимума или максимума) линейных функций нескольких переменных при линейных ограничениях, налагаемых на переменные.

По типу решаемых задач методы линейного программирования разделяются на два вида: универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Особенностью задач ЛП является то, что целевая функция достигает экстремума на негладкой границе области допустимых решений.

Излагаемый материал основан на работах [1 – 3].

1. Постановка задачи

Прежде чем перейти к формальной теории, рассмотрим пример. Небольшая фабрика изготавливает два вида красок: для внутренних (K₁) и наружных работ(K₂). Для производства красок используется два исходных продукта A и B. На фабрике имеются: емкость для хранения продукта A вместимостью 8т; емкость для продукта B вместимостью 6т. Ежесуточно перед работой емкости с продуктами A и B наполняются полностью. Для производства 1т краски K₁ расходуется 1/3т продукта A и 2/3т продукта B. Для производства 1т краски K₂ расходуется 2/3т продукта A и 1/3т продукта B. Краски K₁ и K₂ продаются на оптовом рынке по цене 2 и 3 денежные единицы за тонну соответственно.

Изучение сбыта показало, что суточный спрос на краску K₁ может превосходить спрос на краску K₂ не более чем на 3 тонны. Кроме того, спрос на краску K₁ не превышает 6т в сутки.

Какое количество краски каждого вида должна за сутки производить фабрика, чтобы выручка от продажи была максимальной? Предполагается, что в пределах ограничений краска продается полностью.

2. Построение математической модели

Для построения математической модели задачи линейного программирования нужно ответить на три вопроса

1. Какие переменные величины должны быть определены?

2. В чем состоит цель? Какая функция (целевая функция) переменных задает величину достижения цели?

3. Каким ограничениям должны удовлетворять переменные?

В рассматриваемом примере имеем.

1. Руководству фабрики требуется определить:

x₁ – объем производства краски K₁;

x₂ – объем производства краски K₂.

2. Цель – увеличение выручки. Целевая функция – объем выручки

.

Требуется максимизировать целевую функцию.

3. Ограничения. По запасу продукта A. При плане (x₁, x₂) выпуска краски, будет израсходовано продукта A. Суточный запас этого продукта составляет 8т, следовательно, за сутки нельзя израсходовать более этого запаса. Получаем неравенство

.

Аналогично по продукту B получаем неравенство

.

Из соотношения спроса на K₁ и K₂ получаем

.

Из ограничения на суточный спрос краски K₁ получаем

.

Так как нельзя произвести отрицательное количество краски, то

.

Все вместе будет иметь следующий вид

(1.1)

Полученная задача является стандартной задачей на максимум. В общем виде стандартная задача на максимум имеет вид

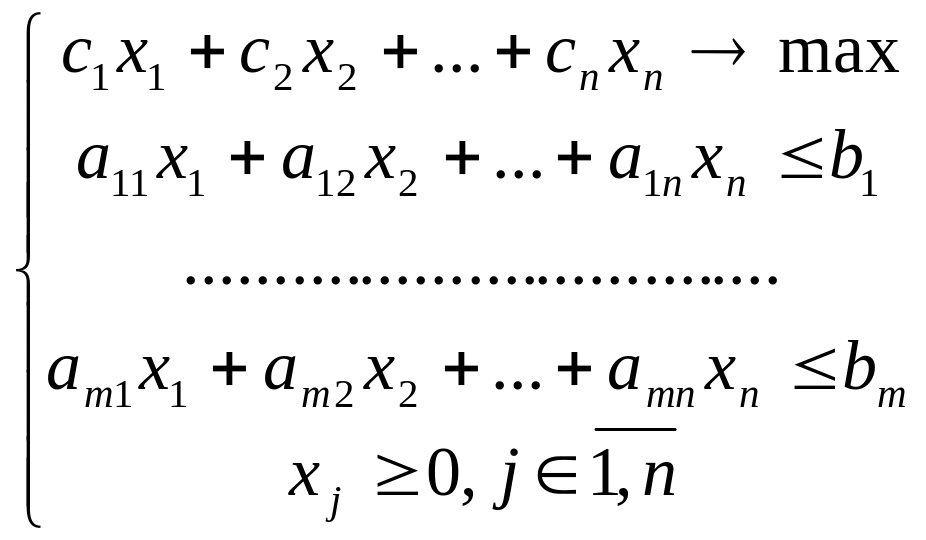(1.2)

Стандартная задача на минимум имеет вид

(1.3)

Общая задача линейного программирования имеет вид

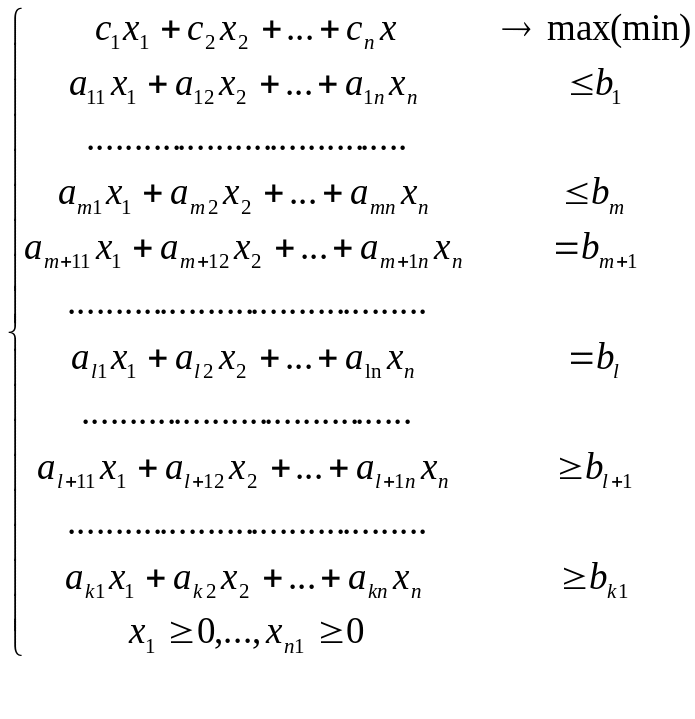(1.4)

Здесь x_j – произвольного знака при . Таким образом, первые m ограничений являются неравенствами типа ≤; ограничения с номерами от m+1 до l – равенства; ограничения с номерами от l +1 до k являются неравенствами типа ≥.

Определение 1.2.1. Линейная функция называется целевой функцией.

Определение 1.2.2. Множество X всех точек , удовлетворяющих ограничениям задачи ЛП, называется допустимым множеством, а любая точка x X называются допустимым планом.

Задача линейного программирования состоит в нахождении допустимого плана, доставляющего максимум (минимум) целевой функции на множестве допустимых планов.