Модальные регуляторы имитирующие модель в пространстве состояний

Выходной сигнал y(t) модели формируется кaк C*x(t). Сигнал управления u(t) модального регулятора вычисляется как -K*x(t), т.е. аналогично выходному сигналу. Поэтому естественным будет реализация модального регулятора в виде дополнительного выхода модели. Строка коэффициентов К регулятора вводится дополнительной строкой в матрицу C модели, для которой производился расчёт модального регулятора

C2 = [C; K].

Здесь знак ; вызывает перевод строки. Матрица K без минуса, чтобы потом использовать отрицательную обратную связь.

Для наблюдаемой столбцевой присоединённой канонической формы модальный регулятор также может быть вычислен как разность коэффициентов полиномов желаемого и действительного. Но такой регулятор может быть включён в модель объекта в виде дополнительного столбца L

L = (polg – polo)’

в матрицу B, т.е. в виде дополнительного входа

B2 = [B, L].

Контур управления с таким модальным регулятором формируется отрицательной обратной связью с выхода y(t) модели на дополнительный вход.

После преобразования управляемой строчной в наблюдаемую столбцовую присоединённую каноническую форму можно сформировать модель с встроенными модальными регуляторами K, L в виде дополнительного выхода и входа.

Структурная схема модели с двумя встроенными модальными регуляторами в виде дополнительного входа и выхода изображена на рис. 2.

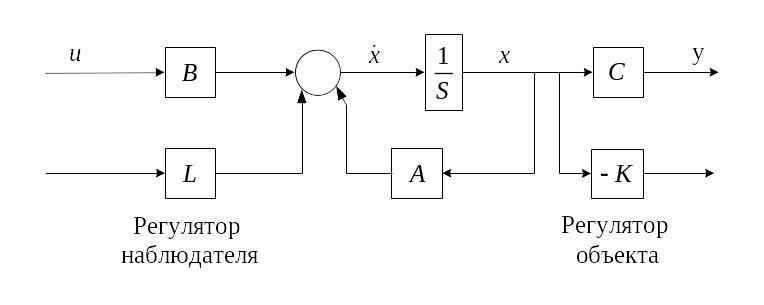
Рис. 2. Структурная схема модели с двумя встроенными модальными регуляторами

Можно не преобразовывать модель в канонические формы, а вычислить столбец L как

L = acker(A’, C’, pg)’.

Пояснения к тексту программы modals01

Программа modals01 выполняется автоматически. Переход к очередному шагу осуществляется нажатием любой клавиши. В дополнение к теоретическим сведениям приведем пояснения к тексту программы modals01 и формированию управляемой строчной и зеркальной ей наблюдаемой столбцовой присоединенной формы.

Выходы интеграторов являются переменными x(t) вектора состояния модели. Если нумерацию переменных x(t) проводить по ходу прохождения сигнала, то цепочка интеграторов в матрице A отразится диагональю (№ -1) из n-1 единиц ones(1,n-1) под главной диагональю

A0 = diag(ones(1, n-1),-1).

Подключение к входу первого интегратора цепочки отражается единицей в первой строке матрицы B. Остальные интеграторы с входом непосредственно не связаны, поэтому остальные элементы столбца B нулевые

B0 = [1;zeros(n-1,1)].

Подключение к выходу последного интегратора цепочки отражается единицей последнего элемента строки матрицы C. Остальные интеграторы с выходом непосредственно не связаны, поэтому остальные элементы строки C нулевые

C0 = [zeros(1,n-1),1].

Непосредственной связи входа и выхода нет, поэтому матрица D нулевая

D0 = 0.

Собрав модель Mss

Mss0 = ss(A0, B0, C0, D0),

можем убедиться в её правильности по передаточной функции

zpk(Mss0),

представляющей собой произведение n интегральных звеньев с коэффициентом единица.

Цепочка интеграторов охватывается отрицательными обратными связями по переменным x(t) если обратные связи с выходов интеграторов сходятся в одной точке (на входе первого интегратора), то их коэффициенты отражаются в первой строке матрицы А.

Чтобы не стирать матрицу A0 сделаем её копию A1 и A2

A1 = A0, A2 = A0.

Пусть нам известна желаемая передаточная функция Mtf модели n-го порядка, и полиномы её числителя и знаменателя легко вычисляются

[ch, zn] = tfdata(W, ‘v’).

где полином знаменателя n-го порядка будет записан с коэффициентом 1 при старшей степени

zn = [1 a1 a2 a3 …an].

Мы должны сделать его характеристическим полиномом модели. Для этого в матрице A заменяем первую строку коэффициентами полинома, от второго до последнего коэффициента, со знаком минус

A1(1,:) = - zn(2:end).

Таким изменением матрицы A обеспечиваются желаемые полюса модели. Для введения нулей необходимо изменить матрицу B или C. Если оставим неизменной матрицу B, то получим управляемую каноническую форму, что предпочтительней для расчёта регулятора. Для введения нулей в матрицу C записываем коэффициенты числителя передаточной функции

C1 = ch.

Собрав модель Mss1 с обновлёнными матрицами A и C

Mss1 = ss(A1, B, C1, D),

получим управляемую строчную присоединённую каноническую форму модели Mss1 и можем убедиться в соответствии её передаточной функции

tf(Mss1) zpk(Mss1).

Таким образом, управляемую строчную присоединённую каноническую форму модели легко записать по передаточной функции без каких либо вычислений.

Модель с встроенным регулятором в виде дополнительного выхода Mss2 будет сформирована командой

Mss2 = ss(A, B, C2, 0).

Замкнуть обратную связь можно командами feedback или connect

Mss2z = feedback(Mss2, 1, 1, 2)

где индексы 1, 2 указывают, что замыкается на первый вход Mss2 второй выход (с регулятором K).

Mss2z = connect (Mss2, [1 -2], 1, [1 2]).