4. Метод кусково-лінійної апроксимації

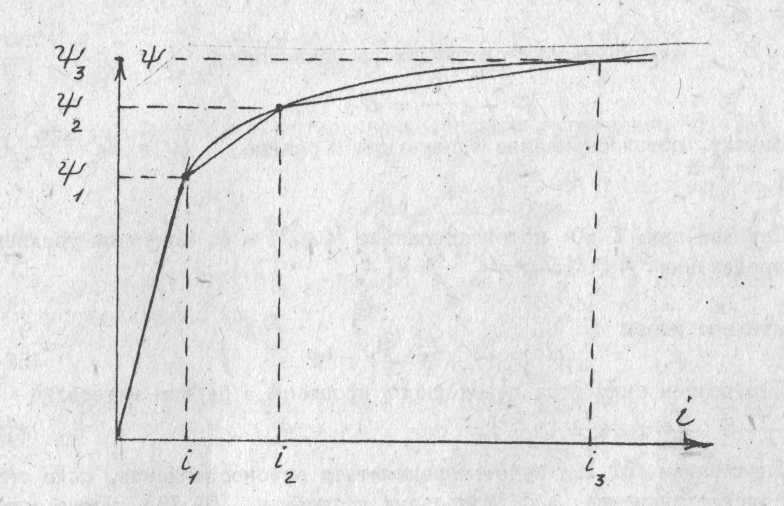Зобразимо вебер-амперну характеристику на рис. 51.10 у вигляді сукупності прямолінійних відрізків.

Рис. 51.10

Для кожного інтервалу залежність між потокозчепленням і струмом лінійна. Її можна визначити формулою:

для 0≤ ψ ≤ ψ₁, ψ = L₁ i,

де L₁= ψ_1/ i;

для другого інтервалу ψ₁≤ ψ ≤ ψ₂ , ψ= ψ₁+ (i-i₁ ) L₂ (51.10)

де ; (51.11)

для третього інтервалу ψ₂≤ ψ; ψ= ψ₂+ (i-i₂ ) L₃. (51.12)

де . (51.13)

При підключенні нелінійного кола під сталу напругу (див. рис. 51.3) рівняння рівноваги має вигляд

. (51.14)

В момент підключення кола ψ(0) =0, і розрахунок перехідного процесу для першого інтервалу можна виконати, вважаючи, що коло лінійне, a індуктивність незмінна й дорівнює величині L_1. Так як U постійне, то з виразу (51.14) отримаємо значення потокозчеплення для сталого режиму:

ψ₁΄=U₀ L₁/R.

Вільна складова ψ₁΄΄ змінюється за законом експоненти:

, де P₁ - корінь характеристичного рівняння.

Виходить, потокозчеплення в перехідному режимі .

Так як при t=0 потокозчеплення ψ(0)=0, отримуємо рівняння для визначення А: 0=U₀ L₁ /R + А₁.

Остаточно маємо 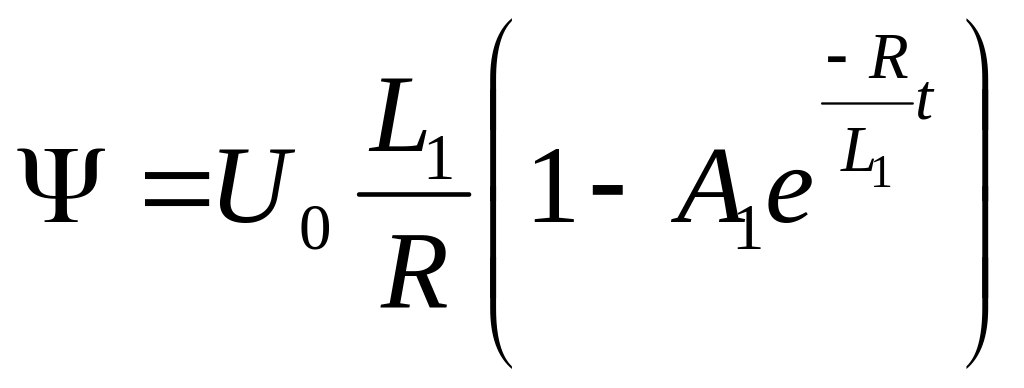. (51.15)

Визначаємо силу струму перехідного процесу на першому інтервалі

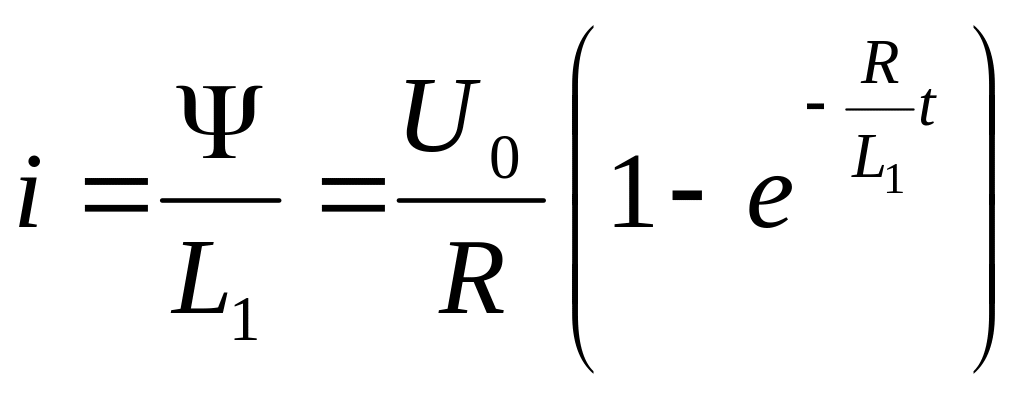. (51.16)

Вираз (51.15) буде визначати потокозчеплення, поки воно не досягне значення ψ_1. Використовуючи рівняння (51.15), можна визначити час, t₁ коли потокозчеплення стане рівним ψ_1.

. (51.17)

На другому інтервалі рівняння рівноваги кола має вигляд

.

Розв’язуючи це рівняння відносно ψ, отримуємо ψ₂΄=U₀ L₂ / R.

Складова вільного режиму визначається аналогічно:

_, де .

Потокозчеплення на другому інтервалі визначається формулою

. (51.18)

Для визначення коефіцієнта А₂ скористаємося принципом неперервності магнітного потоку. У момент t₁ величина потокозчепленням дорівнює ψ_1. Використовуючи цю умову, з формули (51.18) при t= t₁ отримуємо

Таким чином 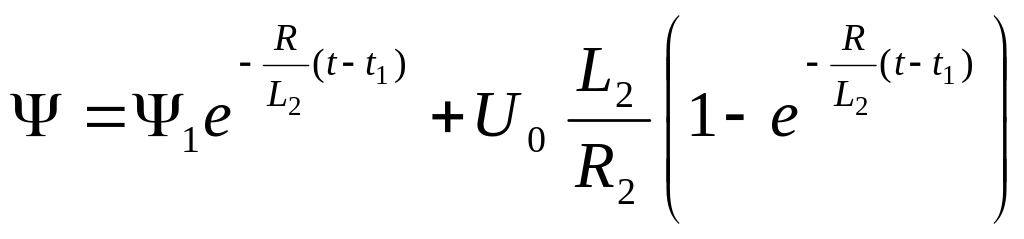. (51.19)

Силу струму на другому інтервалі отримуємо з рівнянь (51.11) і (51.19) .

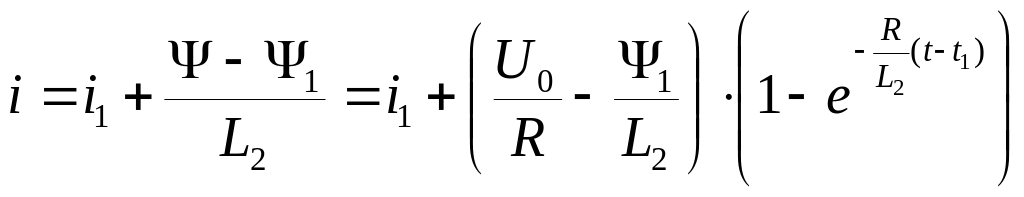(51.20)

З рівняння (51.19) визначаємо час t₂, коли потокозчеплення досягне величини ψ₂

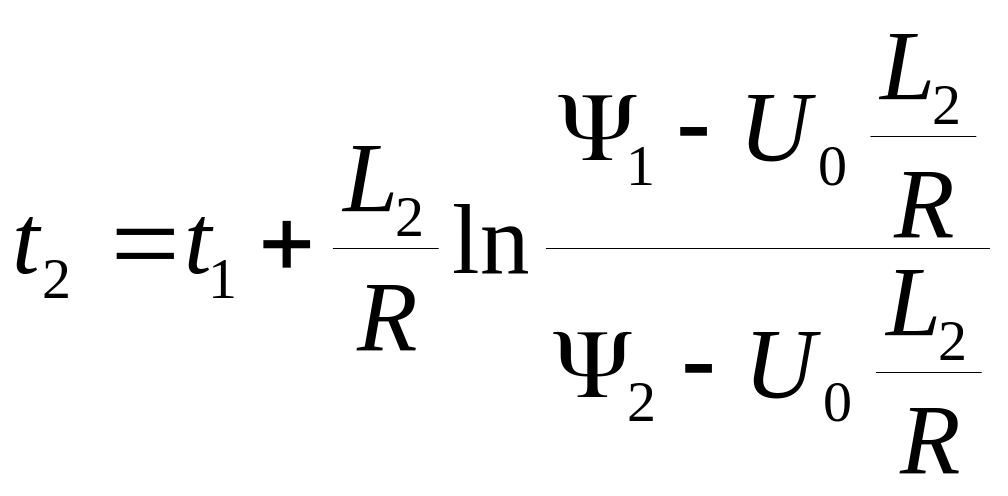(51.21)

Для третього інтервалу розрахунок виконуємо аналогічно, а формули мають вигляд

; (51.22)

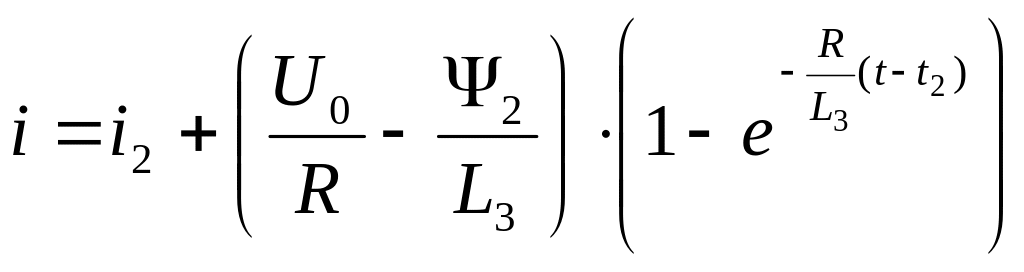. (51.23)

. Розрахунок перехідного процесу варто виконувати в такій послідовності:

1. апроксимувати вебер-амперну характеристику котушки, що досліджується прямолінійними відрізками;

2. визначити індуктивності на кожній ділянці по формулах (51.10), (51.12),(51.13);

3. використовуючи формулу (51.17), розрахувати час t₁ ;

4. вибравши інтервал ∆t (наприклад ∆t=t₁/10) по формулах (51.15),(51.16), розрахувати потокозчеплення й силу струму;

5. перехідний процес на другому інтервалі розрахувати в такій же послідовності, використовуючи формули (51.21), (51.19), (51.20). Інтервал ∆t вибирається виходячи із тривалості інтервалу t₂ – t₁ і бажаної кількості розрахункових точок;

6. третій інтервал розрахувати по формулах (51.22) і (51.23).

Результати розрахунків рекомендується звести в таблицю. Графіки побудувати на одному рисунку з експериментальною кривою струму.

Для суміщення теоретичних і експериментальних кривих необхідно:

1. визначити масштаби експериментальної кривої (по осі ординат – вимірювана величина, по осі абсцис – час);

2. розрахувати значення функції залежно від аргументу і, розділивши їх на масштаби, отримати відрізки і відповідні точки, сукупністю яких визначається теоретична крива.

Лабораторна робота №52

ДОСЛІДЖЕННЯ ОДНОРІДНОЇ СИМЕТРИЧНОЇ ЛАНЦЮГОВОЇ СХЕМИ

Короткий зміст роботи

Дослідним шляхом визначають параметри однієї ланки ланцюгової схеми; обчислюють характеристичний опір і сталу передачі ланцюгової схеми; досліджують розподіл напруг і струмів уздовж схеми при різних режимах; обчислюють довжину й коефіцієнт поширення кабельної лінії, яку моделює дана ланцюгова схема; вивчають розподіл напруг і струмів уздовж лінії.

Підготовка до роботи

При підготовці до роботи необхідно вивчити рекомендовану літературу, ознайомитися з методичними вказівками, описом лабораторної установки, робочим завданням, підготувати протокол звіту на наступні питання:

1. Що таке ланцюгова схема?

2. Яка ланцюгова схема називається однорідною симетричною?

3. Для чого використовуються ланцюгові схеми?

4. Як взаємозв’язані характеристичні опори однорідної симетричної ланцюгової схеми і її однієї ланки, стала передачі схеми і однієї ланки?

5. При яких умовах ланцюгова схема й довга лінія еквівалентні?

6. Що таке режим узгодженого навантаження ланцюгової схеми (еквівалентної довгої лінії)?

7. Записати рівняння ланцюгової схеми й лінії в режимах н.х., к.з., узгодженого навантаження?

8. Як змінюються діючі значення напруг і струмів уздовж лінії в режимах н.х., к.з., узгодженого навантаження?

9. Що таке вхідний опір ланцюгової схеми (лінії)?

10. Як змінюється вхідний опір лінії в режимах н.х., к.з., узгодженого навантаження?

11. Який характер носить вхідний опір лінії на протязі першої чверті довжини хвилі від кінця в режимах н.х., к.з.?

Опис лабораторної установки

Лабораторна установка складається з набору вимірювальних приладів (двох вольтметрів, амперметра, фазометра й фазопокажчика ), регульованого джерела змінної напруги (лабораторного автотрансформатора) і ланцюгової схеми з восьми однакових ланок. Кожна ланка ланцюгової схеми являє собою симетричний П-подібний чотириполюсник. Як навантаження ланцюгової схеми використається активно-ємнісний двополюсник.