Завдання для навчально-дослідної роботи

1. Розрахуйте перехідний процес у колі з послідовним з’єднанням R, С та нелінійною індуктивністю при підключенні до синусоїдної напруги.

2. Дослідіть перехідний процес: у колі на рис. 51.2, якщо кількість витків котушки індуктивності з феромагнітним осердям буде менше (більше) у два рази.

3. Розрахуйте перехідний процес у колі, зображеному на рис. 51.2, якщо перетин феромагнітного осердя буде у два рази меншою початкового.

4. Розрахуйте перехідний процес за схемою на рис. 51.4 аналітичним методом.

Методичні вказівки

Найбільше поширення у колах з великими струмами мають індуктивності, до складу яких входять феромагнітні осердя. Такі елементи мають нелінійні властивості, тому що в рівнянні зв'язку між потокозчепленням і струмом ψ = Li коефіцієнт L не залишається сталим і залежить від сили струму котушки.

Для розрахунку перехідного процесу в колі з нелінійною індуктивністю повинна бути відома залежність між потокозчепленням і струмом. Її можна визначити експериментально за схемою, показаною на рис. 51.1. Якщо до обмотки W₁ підведена синусоїдна напруга, то магнітний потік у феромагнітному осерді є також синусоїдним. Напруга, яка індукується в обмотці W₂, визначається з виразу

,

де Ф₀ - потік у феромагнітному осерді.

Якщо опір R₂ та ємність С є великими за значенням, то струм в обмотці W₂:

.

Тоді напруга на конденсаторі С:

,

звідси

. (51.1)

Маючи залежність i(t) і визначивши ψ=W₁Ф₀= ƒ (t), можна побудувати ψ(t). Залежності i(t) і ψ(t) показані на рис. 51.5. Крива струму I (див. рис. 51.5) отримана експериментально при максимальній синусоїдній напрузі. Крива 2 (див. рис. 51.5) повинна бути побудована на підставі експериментальної кривої U_C (t) і формули (51.1).

Р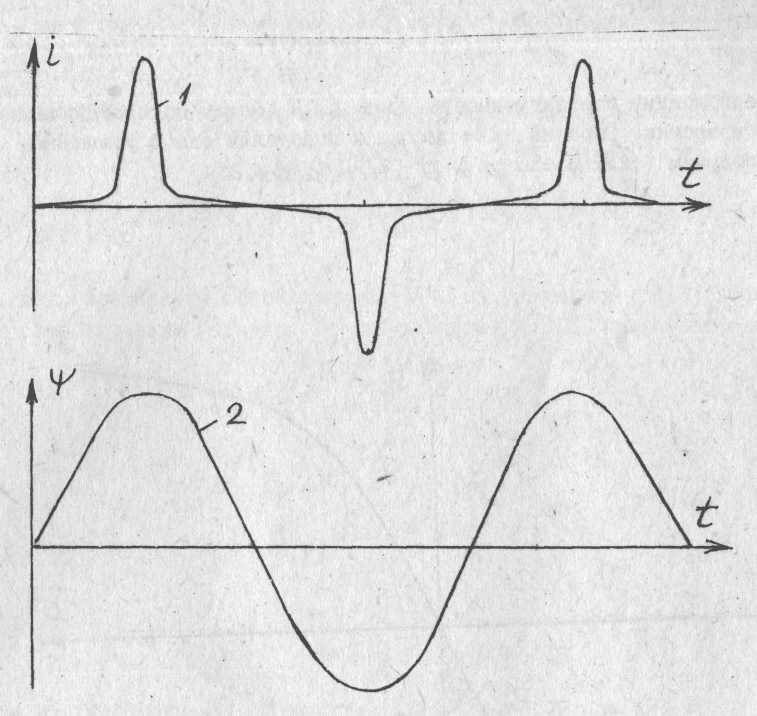 ис. 51.5

При побудові ψ(t) використати масштаб часу експериментальних кривих, що отримують за схемою (див. рис. 51.I). Щоб побудувати ψ(i), розділимо період функції струму і потокозчеплення ψ на ряд інтервалів. Визначаючи для кожного моменту часу струм (крива 1) і потокозчеплення ψ (крива 2, див. рис. 51.5), у новій системі координат будуємо залежність ψ(i) (рис. 51.6). Явищем гістерезису знехтувати.

Залежність ψ(i) можна побудувати також на підставі амплітудних значень напруги й сили струму котушки за результатами досліду п. 2 робочого завдання.

Для розрахунку перехідних процесів у нелінійних електричних колах використовують різні методи.

1. Метод умовної лінеаризації розглянемо на прикладі підключення котушки під синусоїдну напругу.

Рівняння рівноваги електричного кола після підключення під напругу набуває наступного вигляду

. (51.2)

Припустимо, що залежність ψ=Li між потокозчепленням і струмом відома. Виразивши й підставивши його в рівняння (51.2), одержимо .

Р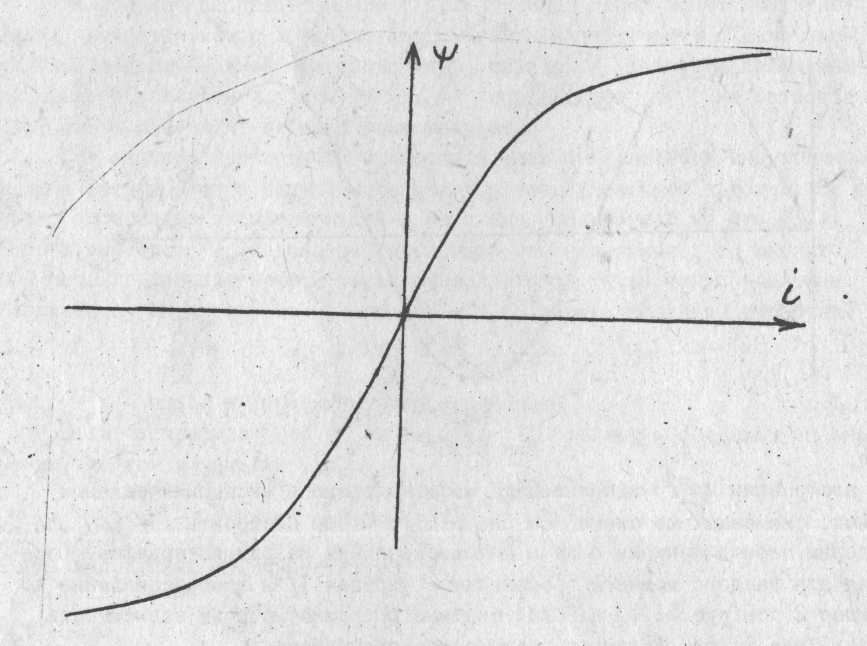 ис. 51.6

Так як другий член рівняння малий, то, припускаючи, що він незмінний по величині, отримаємо лінійне неоднорідне диференціальне рівняння першого порядку. Повне його рішення визначається сукупністю двох складових частин ψ' й ψ''. ψ = ψ' + ψ'' = ψ_M sin (t + β)+ Аe^pt ;

ψ'' є загальним рішенням однорідного диференціального рівняння.

;

ψ' є частковим рішенням неоднорідного диференціального рівняння

(51.3)

Для визначення складової ψ' з рівняння (51.3) скористаємося символічним методом. Тоді рівняння (51.3) приймає наступний вид:

(51.4)

або

.

Позначимо ,

де .

Тоді з рівняння (51.4) маємо .

З останнього виразу знаходимо .

Складова потокозчеплення сталого режиму як функція часу визначається виразом .

Для визначення ψ'' необхідно скласти характеристичне рівняння , звідки .

Тоді , і повне потокозчеплення перехідного процесу визначається виразом .

Для визначення коефіцієнта A скористаємося початковими умовами. В момент комутації - при t = 0 потокозчеплення котушки дорівнює нулю. Значить і вираз, потокозчеплення перехідного процесу має вигляд (51.5)

Рівняння (51.5) можна представити виразом ƒ(t)=a sin(t+b)- c e^-kt.

З виразу (51.5) видно, що складова вільного режиму залежить від початкової фази синусоїдної напруги α. Якщо α - φ = 0, то в колі відразу наступає сталий режим.

При розрахунку ψ по виразу (51.5) значення L визначити графічно, використовуючи початкову ділянку залежності ψ(i) (див. рис. 51.6).

Н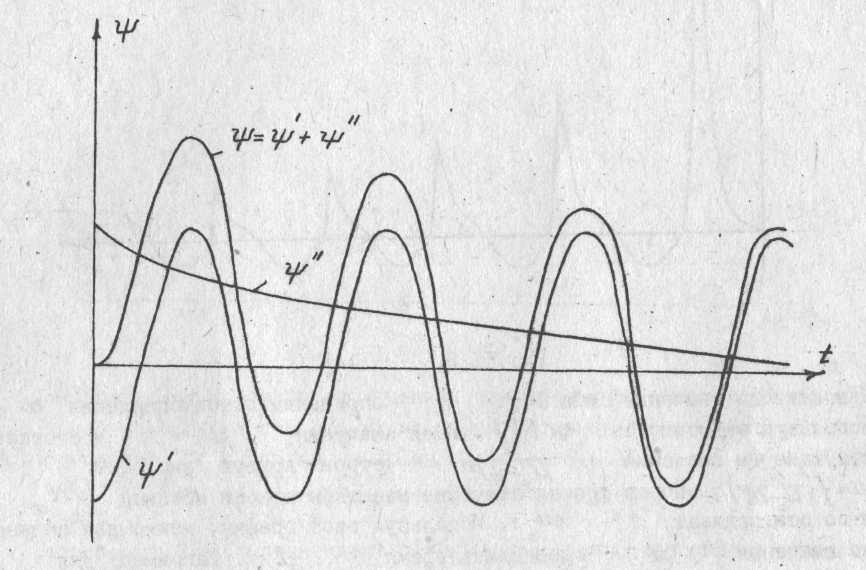 а рис. 51.7 показана залежність ψ(t) для випадку, коли  - φ = π/2. По кривій ψ(t) і ψ(i) можна побудувати криву струму i(t) яка показана на рис. 51.8.

Рис.51.7