2. Преобразование схем замещения
2.1. Основные расчетные приемы
Если схема замещения не содержит замкнутых контуров и в ней имеется один или несколько источников ЭДС, то ее необходимо привести к простейшему виду путем элементарных преобразований как в обычных расчетах линейных электрических цепей. К ним относятся, например: замена нескольких генерирующих ветвей, присоединенных к общему узлу, одной эквивалентной; преобразования треугольника в звезду и обратно и т. д.
Эквивалентные преобразования схем замещения приведены в таблице 2.1.
Таблица 2.1
Эквивалентные преобразования схем замещения
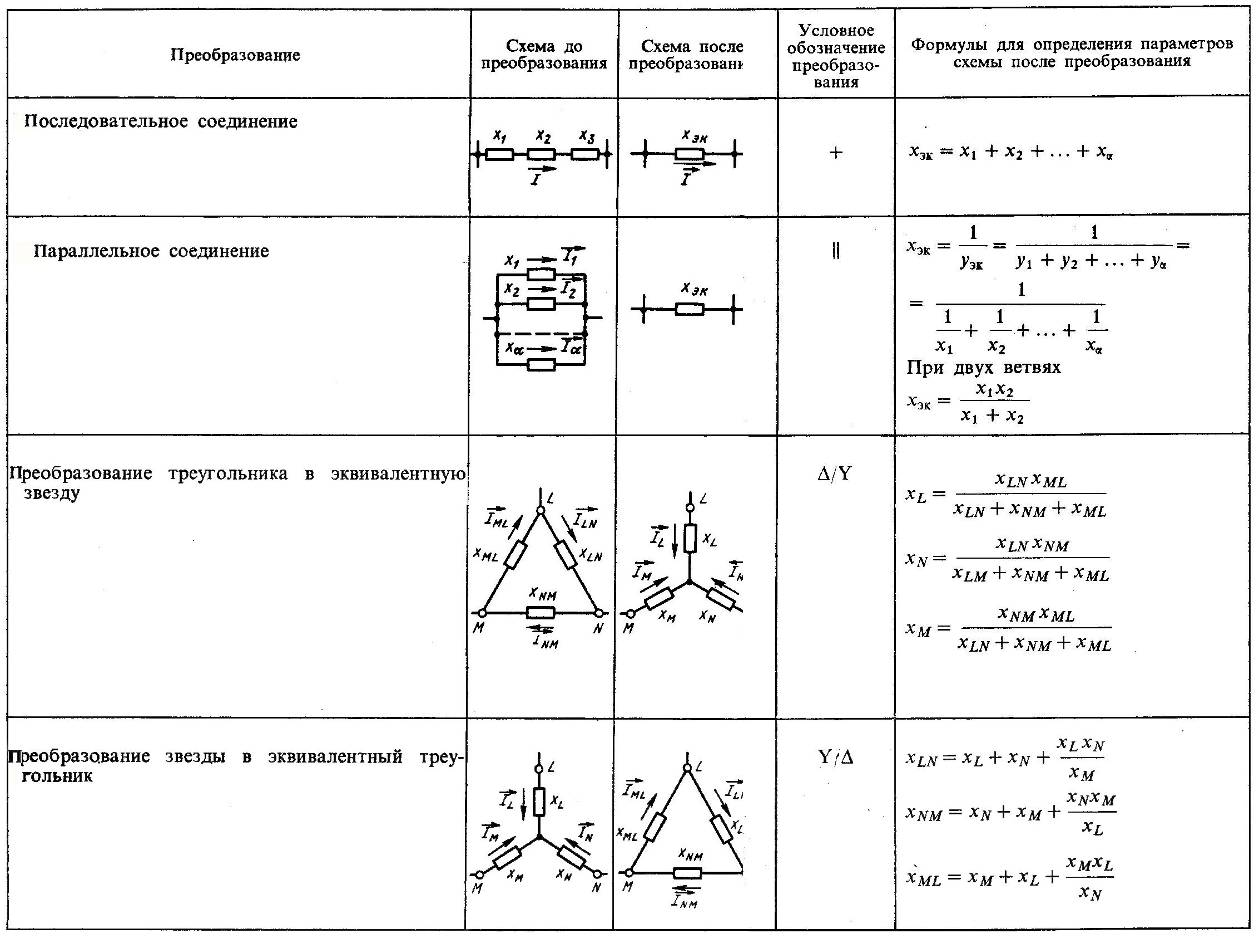
Окончание табл. 2.1
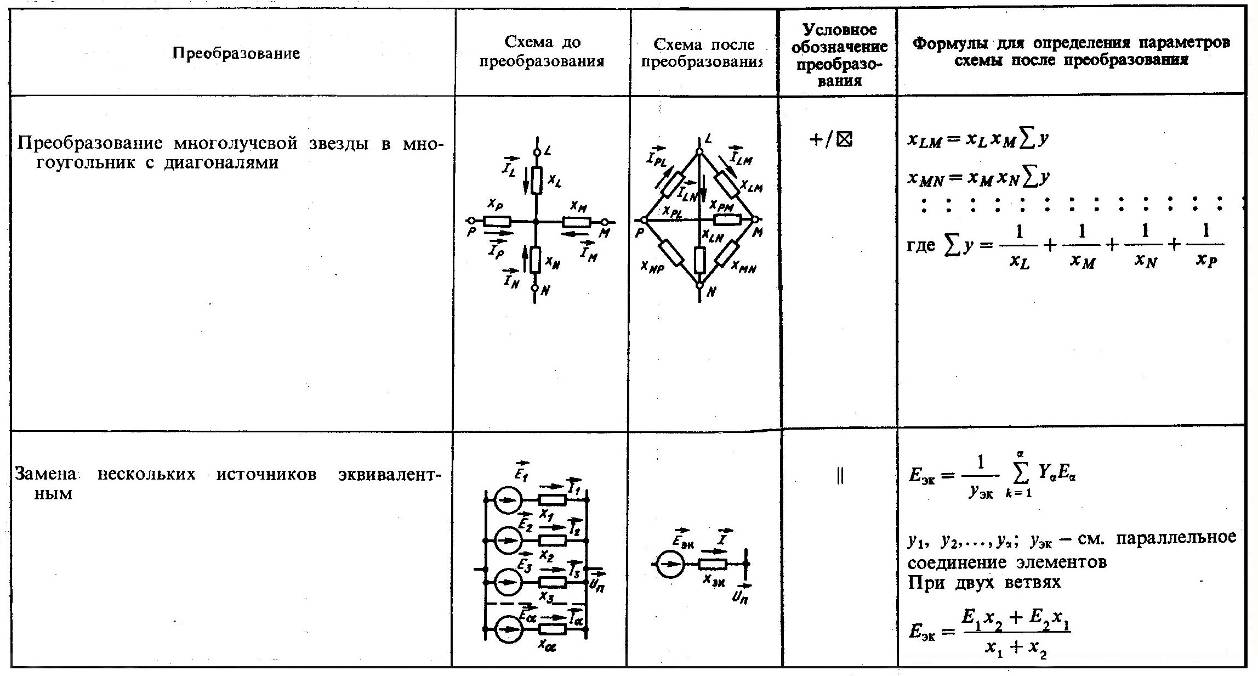
Эквивалентная замена генераторных ветвей одним эквивалентным генератором возможна, если:
1. Генераторы, питающие точку КЗ, однотипные (турбогенераторы или гидрогенераторы).
2. Генераторы, питающие точку КЗ, соизмеримой мощности и имеют соизмеримую удаленность от точки КЗ.
Определение взаимных сопротивлений, например, между источником и точкой КЗ при преобразовании схемы к радиальному (лучевому) виду (рис. 2.1).
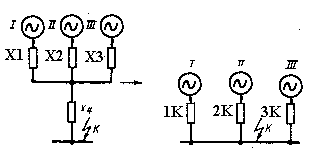
Рис. 2.1. Преобразование схемы
Порядок преобразования схемы следующий:
,
,
,
,
.
Проверка:
С1 + С2 + С3 = 1.
,
,
.
При преобразованиях схем в ходе выполнения расчетов нужно учитывать некоторые специфические особенности:
1. Первоочередной задачей расчета тока КЗ является определение тока непосредственно в аварийной ветви или в месте КЗ. Поэтому преобразование схемы нужно вести так, чтобы аварийная ветвь, по возможности, была сохранена до конца преобразования или, в крайнем случае, участвовала в нем на последнем этапе.
С этой целью, в частности, концы нагрузочных ветвей, ЭДС которых принимаются равными нулю, следует соединять с точкой КЗ (рис. 2.2).
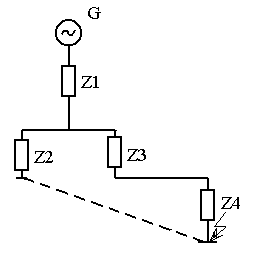
Рис. 2.2. Преобразование схемы
2. Когда КЗ находится в узле с несколькими сходящимися в нем ветвями, этот узел можно разрезать, сохранив на конце каждой образовавшейся ветви такое же КЗ. Далее полученную схему нетрудно преобразовать относительно любой из точек КЗ, учитывая другие ветви с КЗ как нагрузочные ветви с ЭДС, равными нулю (рис. 2.3).
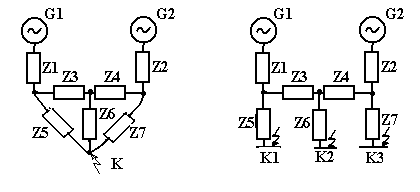
Рис. 2.3. Преобразование схемы
Такой прием эффективен, когда нужно найти ток в одной из ветвей, присоединенных к узлу КЗ.
Определенные трудности в упрощении схем возникают, когда точка КЗ находится в одном из узлов многоугольника, к другим узлам которого присоединены генерирующие ветви (рис. 2.4).
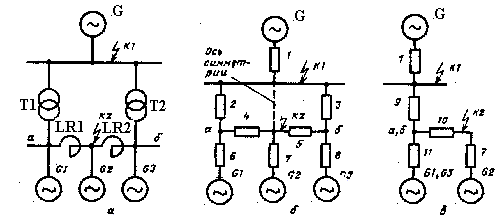
Рис. 2.4. Преобразование схемы
Если
точка КЗ делит схему на две симметричные
части, например, точки К1, К2,
то при одинаковых характеристиках
генераторов G1, G3
и трансформаторов узлы а и b
схемы будут иметь одинаковые потенциалы,
вследствие чего их можно совместить:
ветви генераторов G1
и G3 объединяют,
представляя их эквивалентной машиной
с S = 2Sном.
В результате получится схема «в». В этой
схеме
,
,
.
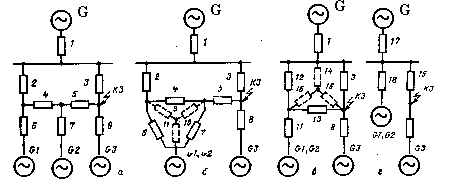
Рис. 2.5. Преобразование схемы
Преобразуем
схему, приведенную на рис. 2.5. Если
генераторы G1 и G2
имеют одинаковые ЭДС, то их можно
объединить в эквивалентный генератор
с мощностью S = 2Sном.
При таком объединении образуется
треугольник сопротивлений Х4, Х6,
Х7 (рис. 2.5 б), который преобразуется
в звезду Х9, Х10, Х11.
Далее преобразовывая, получим:
,
.
Полученный треугольник Х3, Х12,
Х13 преобразуется в звезду Х14,
Х15, Х16 (рис. 2.5 в).
Последовательно сложив сопротивления
и
,
получим схему рис. 2.5 г.
Если схема имеет одинаковые ЭДС, то в некоторых случаях упрощение схемы достигается объединением источников. Например, если схема на рис. 2.7 а имеет одинаковые ЭДС Е2 и Е3, то объединяя эти ЭДС и преобразуя полученный треугольник 2-3-6 в эквивалентную звезду, получим схему (рис. 2.6 б).
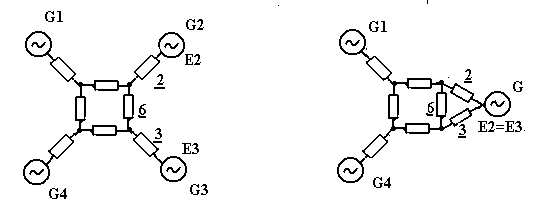
а б
Рис. 2.6. Преобразование схемы
Следует отметить, что трудность преобразования схем замещения в значительной степени определяется выбранным порядком выполнения операций по упрощению схемы. Поэтому при преобразовании схем следует придерживаться такого порядка расчётов и записи результатов, который обеспечивает проверку полученных результатов. После получения простейшей схемы, содержащей точку КЗ и эквивалентную ЭДС, за эквивалентным сопротивлением приступают к расчёту тока КЗ. Токи и напряжения в других ветвях схемы (если в этом есть необходимость) определяют, совершая обратный переход от простейшей схемы к всё более сложным, вплоть до исходной.
Пример 2.1
На рис. 2.7 представлена исходная схема и схема замещения с указанием параметров. Необходимо выполнить преобразование схемы замещения и определить её параметры при КЗ в точках К1 и К2.
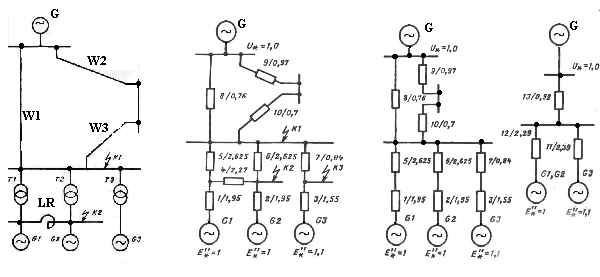
а б в г
Рис. 2.7: а – исходная схема; б – схема замещения; в – схема замещения без учёта реактора; г – упрощённая схема
Решение
КЗ в точке К1.
Ветви генераторов G1 и G2 симметричны относительно точки КЗ К1, поэтому сопротивление реактора Х4 можно исключить из схемы замещения, т. к. оно включено между узлами одинакового потенциала и не влияет на ток КЗ. С учётом этого, схема замещения при КЗ в точке К1 будет иметь вид, показанный на рис. 2.8 в. Упростим схему:
– результирующее сопротивление цепи генератора G3
;
– результирующее сопротивление цепи однотипных генераторов G1 и G2
;
– результирующее сопротивление ветви G (шин неизменного напряжения)
.
Упрощённая схема замещения с указанием параметров представлена на рис. 2.7 г.
КЗ в точке К2 (на выводах генератора G2).
Генератор G3 находится на значительной электрической удалённости от места КЗ, и поэтому для упрощения расчётов его целесообразно включить в состав ветви системы, определив её сопротивление:
.
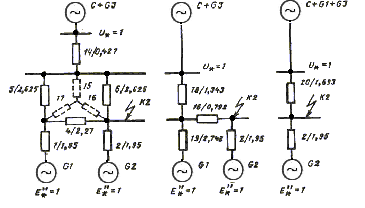
а б в
Рис. 2.8. Схемы замещения для КЗ в точке К2
Ток КЗ в точке К2 от энергосистемы G, генераторов G1 и G3 легче определить, объединив эти источники в единую эквивалентную ветвь. Ветви G и G3 объединены и представлены общим сопротивлением Х14.
Преобразуем треугольник сопротивлений Х4, Х5, Х6 в эквивалентную звезду Х15, Х16, Х17:
,
.
Схема замещения (рис. 2.8 б) преобразуется к виду (рис. 2.8 в), где:
,
.
Конечная схема замещения для расчётов тока КЗ в точке К2 будет иметь вид, представленный на рис. 2.8 г. Сопротивление эквивалентной ветви:
.
Пример 2.2
Для схемы, представленной на рис. 2.9, составить схему замещения и преобразовать её в звезду относительно точки КЗ при следующих данных в относительных единицах: Х1(G) = 0,2; Х2(W1) =0,15; Х3(T) =0,26; Х4(LR)= =0,3; Х5(W2) =0,04; Х6(G1) =0,25; Х7(H) =0,4.
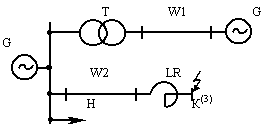
Рис. 2.9. Исходная схема к примеру 2.2
Решение
Схема замещения с величинами сопротивлений приведена на рис. 2.10.
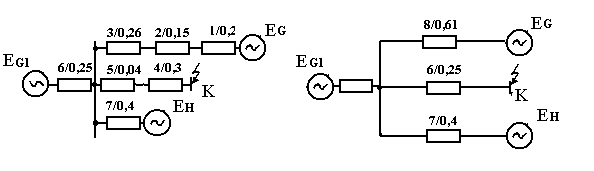
Рис. 2.10. Схема замещения к примеру 2.2
Преобразуем схему замещения в лучевую звезду относительно точки КЗ:
;
;
;
;
;
;
;
;
;
;
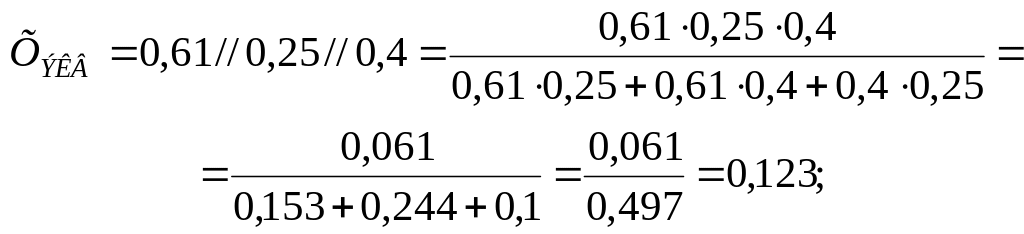
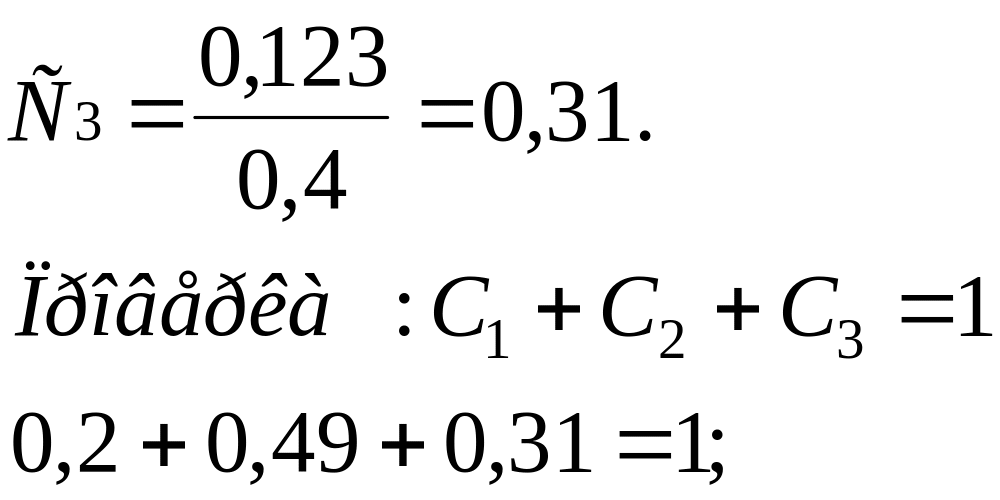После преобразования схема будет иметь вид, представленный на рис. 2.11.
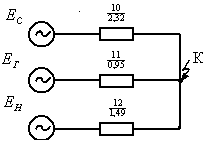
Рис. 2.11. Преобразованная схема