
- •Міністерство освіти і науки України Національний Університет «Львівська політехніка»
- •Лабораторна робота №4
- •Інструкція до лабораторної роботи з курсу “Управління проектами з консолідованою інформацією”
- •Теоретичні основи Метод pert
- •Pert-метод Хід роботи
- •Оцінка тривалості робіт за методом pert
- •Проведення pert-аналізу в ms Project
- •Хід роботи
Хід роботи
Щоб ввести характеристики робіт, а саме песимістичну - b, найімовірнішу - m та оптимістичну - а тривалості для кожної з робіт, необхідно на панелі «Анализ по методу PERT» вибрати пункт «Лист ввода PERT» (рис. 1).
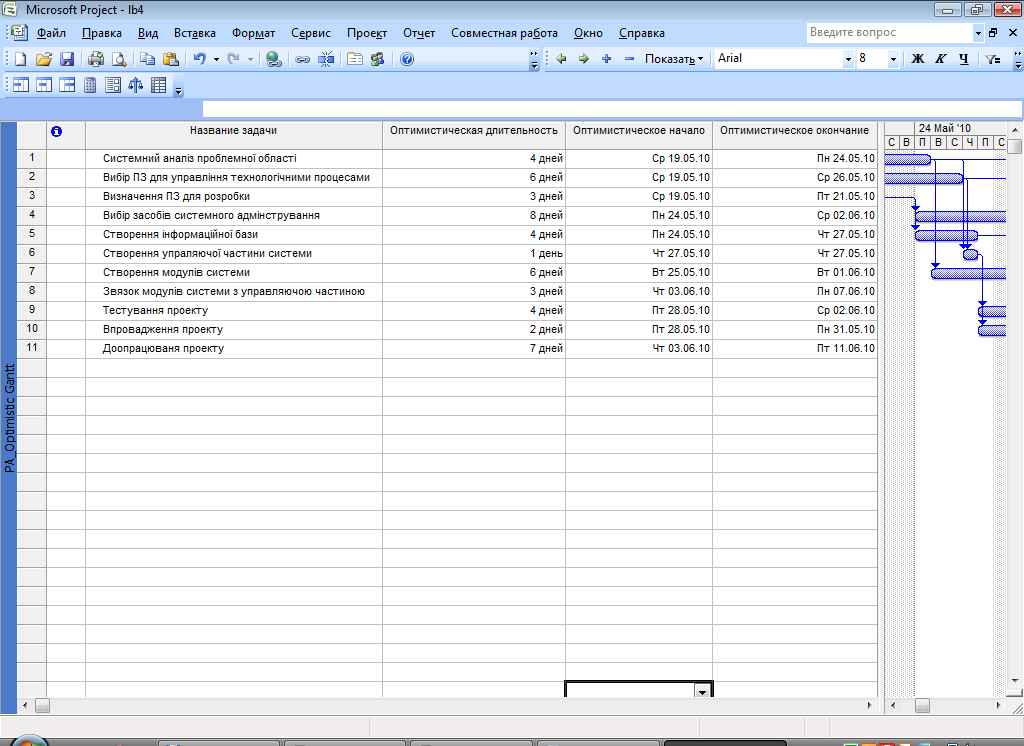

Рис. 1. Панель «Аналізу по методу PERT»
Після введення усіх даних отримуємо три діаграми Ганта песимістичну (рис. 2), оптимістичну (рис. 3) та найімоврнішу (рис. 4).
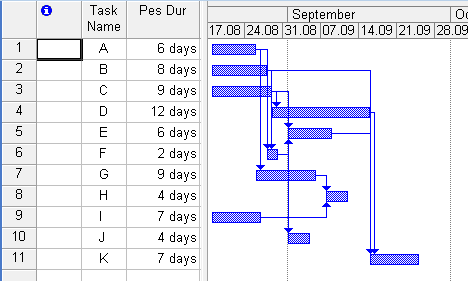
Рис. 2. Песимістична діаграма Ганта
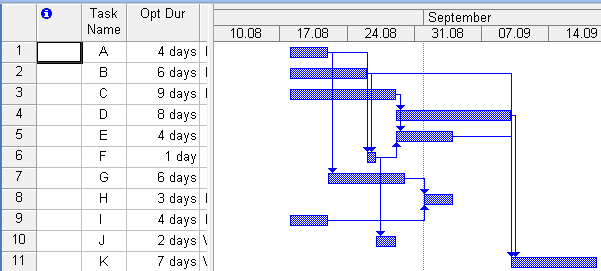
Рис. 3. Оптимістична діаграма Ганта
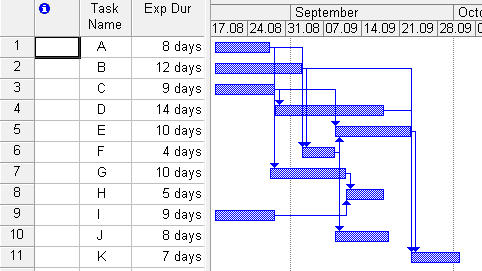
Рис. 4. Найімовірніша діаграма Ганта
Аналізуючи вищенаведені графіки, можемо побачити, що проект буде виконаний при оптимістичних оцінках за 25 дні, песимістичних – 33 дні, найімоврінших – 29. Виходячи з цього можемо побачити що при перевищенні терміну виконання заданому при найімоврнішому прогнозі на 10 днів ми не вкладаємось у песимістичні терміни.
Призначимо ресурси нашим подіям (рис. 5)
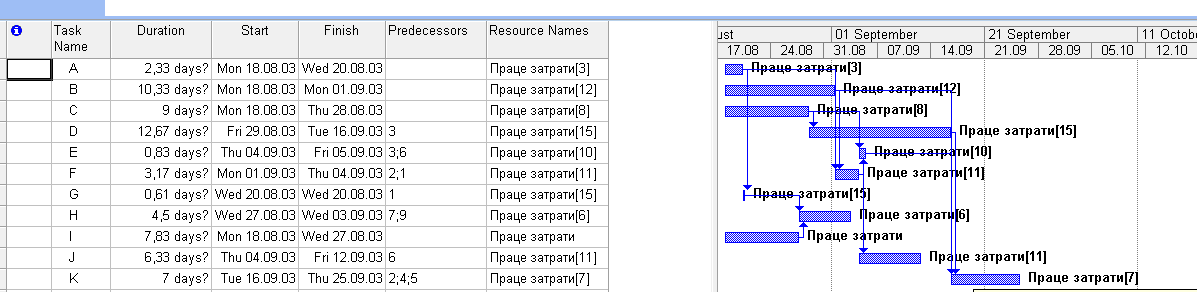
Рис. 5. Ресурси призначені подіям
Проведемо аналіз одного з ресурсів, а саме «Людино-ресурси». Для того, щоб він відповідав нашим вимогам проведемо автоматичнее вирівнювання ресурсів, в результаті якого отримаємо графік ресрсів, зображений на рис. 6.

Рис. 6. Розподіл ресурсу «Людино-ресурси»
Висновок. На даній лабораторній роботі було досліджено основні параметри мережі PERT та реалізації їх розрахунку в програмному пакеті MS Project 2007. Також було вирахувано можливість не вкладення в терміни виконання проекту при збільшенні виконання його середньої тривалості на 10днів Також показано розподіл ресурсу для задач проекту та зроблено автоматичне вирівнювання розподілу цього ресурсу для проекту.
Перелік варіантів
Варіант -1
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку.Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
5 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
4 |
8 |
12 |
7 |
12 |
9 |
12 |
4 |
21 |
9 |
11 |
4 |
12 |
7 |
13 |
8 |
8 |
12 |
8 |
10 |
12 |
6 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Вартість С=60
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -2
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; A<G; C<E,F; G<H; E<J; B<D,G,E,F;
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
5 |
18 |
15 |
7 |
13 |
10 |
6 |
1 |
12 |
7 |
6 |
10 |
8 |
9 |
12 |
7 |
6 |
8 |
4 |
8 |
12 |
8 |
4 |
18 |
20 |
12 |
15 |
8 |
5 |
3 |
12 |
7 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% більшою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
I<H; G<H; B<F,K; D<K; C<E,D; F<I,J; E<K; A<G,F,K.
Тривалості робіт зведені в таблицю - в першому рядку.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
7 |
10 |
5 |
12 |
8 |
4 |
10 |
5 |
9 |
8 |
12 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; F<G; B<C,E,F; C<D. Вартість — на 10% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
7 |
10 |
4 |
10 |
8 |
8 |
6 |
Варт. при макс. трив. |
4 |
17 |
4 |
14 |
3 |
7 |
4 |
Варіант -3
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: G<H; F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
7 |
8 |
5 |
11 |
7 |
9 |
16 |
11 |
17 |
12 |
4 |
7 |
8 |
5 |
11 |
7 |
9 |
16 |
8 |
8 |
10 |
6 |
13 |
4 |
10 |
8 |
10 |
4 |
8 |
12 |
16 |
6 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде рівною середньому її значенню, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
A<G,F,K; B<F,K; C<E,D; G<H; I<H; D<K; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
6 |
5 |
9 |
8 |
10 |
m |
6 |
10 |
6 |
10 |
6 |
2 |
6 |
4 |
6 |
4 |
8 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; D<G; A<D; C<D. Вартість С=70
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -4
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: A<G; F<K; G<I; D<J; C<E,F; G<H; B<D,G,E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
4 |
8 |
5 |
6 |
9 |
9 |
6 |
10 |
7 |
12 |
14 |
8 |
4 |
12 |
8 |
12 |
5 |
10 |
10 |
7 |
6 |
7 |
4 |
12 |
5 |
12 |
6 |
8 |
9 |
12 |
4 |
12 |
12 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
8 |
8 |
4 |
12 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
8 |
6 |
2 |
8 |
4 |
8 |
5 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; B<C,E,F; E<G; C<D. Вартість — на 10% більша від мінімальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
14 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
49 |
14 |
3 |
7 |
4 |
Варіант -5
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; B<D,G,E,F; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
18 |
25 |
16 |
17 |
9 |
16 |
11 |
17 |
12 |
4 |
7 |
9 |
10 |
10 |
8 |
14 |
8 |
22 |
16 |
28 |
4 |
14 |
18 |
12 |
8 |
10 |
12 |
20 |
8 |
8 |
10 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 15% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; I<H; D<K; C<E,D; F<I,J; G<H; A<G,F,K; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
12 |
m |
7 |
8 |
9 |
10 |
6 |
2 |
9 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Вартість С=80
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
20 |
17 |
9 |
22 |
20 |
26 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
8 |
10 |
4 |
14 |
8 |
12 |
4 |
Варіант -6
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,E,F; D<J; A<G; C<E,F; I<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
5 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
4 |
14 |
16 |
10 |
8 |
10 |
5 |
12 |
10 |
17 |
6 |
8 |
7 |
12 |
20 |
10 |
12 |
6 |
8 |
14 |
9 |
12 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F; C<E,D; F<E,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
9 |
12 |
6 |
2 |
9 |
4 |
7 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; E<G; A<D; C<D. Вартість на 10% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
25 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
13 |
7 |
4 |
Варіант -7
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J,K; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
15 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
14 |
10 |
12 |
10 |
8 |
9 |
12 |
10 |
14 |
10 |
14 |
10 |
7 |
8 |
20 |
12 |
20 |
14 |
12 |
8 |
12 |
6 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
8 |
12 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; A<D; C<G,D. Вартість — середня між максимальною та мінімальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
15 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
9 |
Варіант -8
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
5 |
11 |
7 |
9 |
6 |
10 |
15 |
11 |
4 |
10 |
12 |
10 |
9 |
12 |
9 |
12 |
8 |
10 |
8 |
8 |
6 |
10 |
8 |
20 |
9 |
12 |
12 |
15 |
12 |
9 |
12 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та його вартість.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Тривалість — середня між мінімальною та максимальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -9
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: C<A,B; D<G,E;G<H,J,K;A<I,F; E<F; B<E; H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
5 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
4 |
10 |
16 |
10 |
16 |
10 |
18 |
12 |
5 |
20 |
8 |
12 |
6 |
8 |
9 |
20 |
17 |
9 |
6 |
22 |
30 |
10 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
E<H,K; D<E,G;B<E; G<H,K; C<A,B; H<F; A<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: G<B; B<F;A<B,C,E; D<E. Тривалість — на 5% більша за мінімальну.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -10
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: B<E; D<G,E;G<H,J,K;A<I,F; E<F; C<A,B; H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
5 |
9 |
9 |
16 |
17 |
9 |
6 |
11 |
17 |
6 |
4 |
12 |
18 |
9 |
8 |
10 |
18 |
12 |
22 |
10 |
12 |
8 |
8 |
9 |
12 |
16 |
12 |
12 |
8 |
14 |
20 |
12 |
10 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
G<H,K; D<E,G;B<E; C<A,B; E<H,K; H<F; A<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: B<F;A<B,C,E; G<B; D<E. Тривалість на 5% менша за найдовшу.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
10 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -11
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; D<J; A<G; B<D,G,E,F; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
5 |
8 |
6 |
7 |
6 |
14 |
9 |
12 |
4 |
7 |
12 |
10 |
12 |
12 |
14 |
6 |
14 |
18 |
24 |
8 |
14 |
16 |
5 |
16 |
8 |
10 |
12 |
7 |
9 |
12 |
6 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; C<E,D; F<I,J; A<G,F,K; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
12 |
8 |
4 |
10 |
5 |
9 |
8 |
11 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
9 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: F<G; A<D; B<C,E,F; C<D. Вартість С=60
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
24 |
9 |
18 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -12
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; C<E,F; G<H; E<J; A<G; B<D,G,E,F;
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
5 |
18 |
10 |
7 |
8 |
10 |
6 |
3 |
7 |
7 |
6 |
10 |
9 |
10 |
14 |
16 |
10 |
12 |
9 |
14 |
7 |
12 |
5 |
10 |
5 |
10 |
10 |
5 |
6 |
6 |
10 |
21 |
6 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% більшою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
I<H; G<H; B<F,K; D<K; C<E,D; F<I,J; E<K; A<G,F,K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
7 |
10 |
5 |
12 |
10 |
4 |
10 |
7 |
9 |
8 |
12 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; F<G; B<C,E,F; C<D. Вартість — на 5% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
7 |
10 |
4 |
10 |
8 |
8 |
6 |
Варт. при макс. трив. |
13 |
17 |
4 |
14 |
3 |
7 |
7 |
Варіант -13
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<H; G<I; B<D,G,E,F; A<G; C<E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
4 |
8 |
5 |
10 |
5 |
9 |
16 |
11 |
7 |
12 |
4 |
8 |
16 |
10 |
5 |
10 |
18 |
8 |
11 |
14 |
24 |
8 |
4 |
8 |
10 |
10 |
10 |
9 |
16 |
22 |
14 |
12 |
12 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде рівною середньому її значенню, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
A<G,F,K; B<F,K; C<E,D; G<H; I<H; D<K; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
12 |
12 |
9 |
16 |
12 |
4 |
6 |
5 |
9 |
8 |
10 |
m |
6 |
10 |
6 |
10 |
6 |
2 |
6 |
4 |
6 |
4 |
8 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: D<G; A<D; B<C,E,F; C<D. Вартість С=65
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
10 |
3 |
4 |
14 |
3 |
7 |
4 |
Варіант -14
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: A<G; F<K; G<I; D<J; C<E,F; G<H; B<D,G,E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
8 |
6 |
5 |
4 |
9 |
9 |
6 |
11 |
7 |
12 |
14 |
16 |
12 |
5 |
8 |
18 |
9 |
12 |
22 |
14 |
24 |
28 |
8 |
6 |
10 |
4 |
18 |
12 |
10 |
11 |
14 |
12 |
20 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; D<K; A<G,F,K; I<H; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
10 |
10 |
9 |
8 |
10 |
4 |
12 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
8 |
6 |
2 |
8 |
4 |
8 |
5 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; B<C,E,F; E<G; C<D. Вартість — на 5% більша від мінімальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
24 |
14 |
18 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
49 |
14 |
3 |
7 |
4 |
Варіант -15
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; A<G; C<E,F; G<H; B<D,G,E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
18 |
5 |
16 |
7 |
9 |
16 |
11 |
7 |
12 |
4 |
7 |
9 |
10 |
8 |
14 |
18 |
8 |
7 |
14 |
6 |
8 |
14 |
18 |
5 |
16 |
7 |
9 |
16 |
11 |
14 |
12 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 15% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
I<H; D<K; B<F,K; C<E,D; F<I,J; A<G,F,K; G<H; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
16 |
9 |
16 |
10 |
4 |
10 |
7 |
9 |
8 |
12 |
m |
7 |
8 |
9 |
10 |
6 |
2 |
9 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: F<G; A<D; B<C,E,F; C<D. Вартість С=80
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
20 |
24 |
9 |
22 |
20 |
26 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
12 |
10 |
4 |
14 |
8 |
12 |
4 |
Варіант -16
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,E,F; D<J; A<G; C<E,F; I<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
15 |
16 |
17 |
9 |
6 |
4 |
17 |
12 |
14 |
7 |
16 |
10 |
8 |
8 |
12 |
9 |
8 |
21 |
8 |
14 |
14 |
8 |
20 |
20 |
10 |
16 |
12 |
6 |
8 |
20 |
28 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
G<H; I<H; D<K; A<G,F; B<F,K; C<E,D; F<E,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
14 |
9 |
16 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
9 |
12 |
6 |
2 |
9 |
4 |
7 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; A<D; E<G; C<D. Вартість на 5% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
26 |
27 |
9 |
22 |
25 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
14 |
20 |
4 |
14 |
13 |
7 |
4 |
Варіант -17
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J,K; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
10 |
8 |
15 |
16 |
7 |
9 |
6 |
11 |
4 |
12 |
14 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
I<H; B<F,K; G<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
2 |
4 |
3 |
8 |
4 |
1 |
4 |
3 |
4 |
2 |
4 |
b |
8 |
10 |
8 |
12 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; A<D; C<G,D. Вартість — середня між максимальною та мінімальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
11 |
3 |
Варт. при мін. трив. |
16 |
17 |
19 |
22 |
15 |
21 |
15 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
18 |
6 |
Варт. при макс. трив. |
4 |
10 |
14 |
14 |
3 |
7 |
9 |
Варіант -18
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; B<D,G,E,F; D<J; A<G; G<I; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
6 |
8 |
5 |
8 |
7 |
9 |
6 |
10 |
9 |
11 |
4 |
2 |
4 |
3 |
4 |
2 |
4 |
6 |
5 |
4 |
8 |
8 |
4 |
2 |
4 |
6 |
4 |
3 |
3 |
6 |
3 |
4 |
5 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
2 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
2 |
b |
8 |
15 |
9 |
14 |
10 |
7 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та його вартість.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Тривалість — середня між мінімальною та максимальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
26 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
8 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -19
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: C<A,B; G<H,J,K;A<I,F; E<F; B<E; D<G,E;H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
4 |
8 |
5 |
6 |
7 |
6 |
6 |
8 |
17 |
12 |
4 |
6 |
4 |
5 |
6 |
7 |
6 |
12 |
8 |
8 |
24 |
8 |
2 |
8 |
10 |
3 |
10 |
6 |
6 |
12 |
34 |
12 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
G<H,K; C<A,B; E<H,K; D<E,G;B<E; H<F; A<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
4 |
b |
18 |
12 |
12 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: G<B; B<F;A<B,C,E; D<E. Тривалість — на 10% більша за мінімальну.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
28 |
31 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -20
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: B<E; D<G,E;G<H,J,K;A<I,F; E<F; C<A,B; H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
5 |
9 |
9 |
16 |
17 |
9 |
6 |
11 |
17 |
6 |
4 |
10 |
9 |
12 |
16 |
17 |
18 |
6 |
11 |
34 |
6 |
8 |
5 |
12 |
9 |
8 |
34 |
9 |
12 |
22 |
17 |
12 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
G<H,K; D<E,G;B<E; C<A,B; E<H,K; H<F; A<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: B<F;A<B,C,E; G<B; D<E. Тривалість на 20% менша за найдовшу.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
1 |
Варт. при мін. трив. |
22 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
16 |
10 |
7 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
10 |
10 |
5 |
14 |
3 |
7 |
5 |
Варіант -21
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; A<C,G,E,F; C<J; B<G; G<I; D<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
16 |
8 |
5 |
18 |
7 |
9 |
6 |
10 |
9 |
11 |
4 |
8 |
10 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
A<F,K; G<H; I<H; D<F; B<G,F,K; C<E,D; K<I,J; E<F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
2 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
2 |
b |
12 |
15 |
9 |
14 |
12 |
7 |
10 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та його вартість.
Відношення передування: A<D,E,F; F<G; B<C; D<C. Тривалість — середня між мінімальною та максимальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
26 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
8 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -22
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: A<B,C; G<H,J,K;B <I,F; E<F; C<E; D<G,E;H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
11 |
8 |
5 |
6 |
12 |
6 |
6 |
8 |
17 |
12 |
4 |
8 |
8 |
10 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
8 |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
12 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
G<H,K; A<B,C; E<H,K; D<E,G;C<E; H<F; B<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
4 |
b |
12 |
14 |
10 |
16 |
10 |
4 |
10 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: A<B; B<F;G <B,C,E; D<E. Тривалість — на 15% більша за мінімальну.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
28 |
31 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
8 |
14 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -23
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: B<F; E<G,F;G<H,J,K;A<I,D; F<D; C<A,B; H<D.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
5 |
9 |
9 |
6 |
12 |
9 |
6 |
10 |
6 |
6 |
4 |
10 |
10 |
9 |
12 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
5 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
G<H,K; E<F,G;B<F; C<A,B; F<H,K; H<D; A<I,K,D.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
18 |
20 |
12 |
14 |
10 |
4 |
10 |
8 |
9 |
8 |
12 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
8 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: B<A,D,E; A<F; G<A; C<E. Тривалість на 20% менша за найдовшу.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
1 |
Варт. при мін. трив. |
34 |
17 |
13 |
22 |
15 |
21 |
10 |
Макс. трив. |
16 |
10 |
7 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
10 |
10 |
5 |
14 |
3 |
7 |
5 |
Варіант -24
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: G<K; B<D,H,E,G; D<J; A<H; H<I; C<E,G; H<F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
5 |
12 |
7 |
9 |
6 |
10 |
10 |
11 |
4 |
14 |
10 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
18 |
9 |
6 |
8 |
4 |
10 |
14 |
9 |
18 |
14 |
16 |
4 |
7 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
J<I; D<K; A<G,F,K; C<E,D; B<F,K; G<I; F<J,H; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
2 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
2 |
b |
8 |
12 |
9 |
14 |
8 |
7 |
10 |
5 |
9 |
8 |
9 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та його вартість.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Тривалість — середня між мінімальною та максимальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
36 |
34 |
19 |
22 |
15 |
31 |
10 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
18 |
20 |
14 |
14 |
3 |
17 |
4 |
Варіант -25
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: C<G,B; A<H,J,K;G<I,F; E<F; B<E; D<A,E;H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
8 |
8 |
5 |
6 |
10 |
6 |
6 |
12 |
17 |
6 |
4 |
8 |
8 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
17 |
12 |
7 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
A<H,K; C<G,B; E<H,K; D<E,A;B<E; H<F; G<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
4 |
b |
20 |
10 |
12 |
14 |
10 |
4 |
10 |
5 |
9 |
10 |
10 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: G<B; B<F;A<B,C,E; D<E. Тривалість — на 20% більша за мінімальну.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
28 |
31 |
11 |
22 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
13 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
1 |
14 |
3 |
7 |
4 |
Варіант -26
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: B<E; A<I,F; E<F; C<A,B; D<G,E;G<H,J,K; H<F.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
5 |
9 |
9 |
6 |
7 |
9 |
6 |
8 |
7 |
6 |
4 |
10 |
10 |
9 |
12 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
6 |
8 |
4 |
6 |
14 |
2 |
8 |
4 |
6 |
4 |
7 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
C<A,B; E<H,K; H<F; G<H,K; D<E,G;B<E; A<I,K,F.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
9 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої тривалості виконання проекту С визначити оптимальні тривалості всіх робіт та вартість проекту.
Відношення передування: B<F;A<B,C,E; G<B; D<E. Тривалість на 15% менша за найдовшу.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
1 |
Варт. при мін. трив. |
34 |
31 |
9 |
22 |
15 |
24 |
10 |
Макс. трив. |
16 |
10 |
7 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
10 |
10 |
5 |
14 |
3 |
10 |
5 |
Варіант -27
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку.Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
4 |
8 |
5 |
16 |
17 |
9 |
16 |
11 |
17 |
12 |
8 |
8 |
12 |
7 |
12 |
9 |
12 |
4 |
21 |
9 |
11 |
4 |
12 |
7 |
13 |
8 |
8 |
12 |
8 |
10 |
12 |
6 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
8 |
6 |
6 |
8 |
4 |
10 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
9 |
14 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Вартість С=60
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
8 |
8 |
6 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -28
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; A<G; C<E,F; G<H; E<J; B<D,G,E,F;
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
10 |
10 |
5 |
7 |
13 |
10 |
6 |
4 |
12 |
7 |
6 |
10 |
8 |
9 |
12 |
7 |
6 |
8 |
4 |
8 |
12 |
8 |
4 |
18 |
20 |
12 |
15 |
8 |
5 |
3 |
12 |
7 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% більшою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
I<H; G<H; B<F,K; D<K; C<E,D; F<I,J; E<K; A<G,F,K.
Тривалості робіт зведені в таблицю - в першому рядку.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
7 |
12 |
8 |
4 |
10 |
8 |
9 |
8 |
12 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; F<G; B<C,E,F; C<D. Вартість — на 10% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
4 |
3 |
Варт. при мін. трив. |
16 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
8 |
12 |
6 |
10 |
8 |
8 |
6 |
Варт. при макс. трив. |
4 |
17 |
4 |
14 |
3 |
7 |
4 |
Варіант -29
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: G<H; F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
10 |
6 |
5 |
10 |
7 |
9 |
10 |
11 |
17 |
12 |
4 |
7 |
8 |
5 |
11 |
7 |
9 |
16 |
8 |
8 |
10 |
6 |
13 |
4 |
10 |
8 |
10 |
4 |
8 |
12 |
16 |
6 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде рівною середньому її значенню, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
A<G,F,K; B<F,K; C<E,D; G<H; I<H; D<K; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
9 |
10 |
9 |
14 |
10 |
4 |
8 |
5 |
9 |
8 |
10 |
m |
6 |
10 |
6 |
10 |
6 |
2 |
6 |
4 |
6 |
4 |
8 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; D<G; A<D; C<D. Вартість С=70
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
8 |
10 |
4 |
10 |
4 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
4 |
Варіант -30
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: A<G; F<K; G<I; D<J; C<E,F; G<H; B<D,G,E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
6 |
8 |
5 |
6 |
9 |
12 |
6 |
10 |
9 |
12 |
14 |
8 |
4 |
12 |
8 |
12 |
5 |
10 |
10 |
7 |
6 |
7 |
4 |
12 |
5 |
12 |
6 |
8 |
9 |
12 |
4 |
12 |
12 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
10 |
9 |
9 |
10 |
8 |
4 |
12 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
8 |
6 |
2 |
8 |
4 |
8 |
5 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; B<C,E,F; E<G; C<D. Вартість — на 10% більша від мінімальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
14 |
22 |
15 |
21 |
10 |
Макс. трив. |
8 |
10 |
6 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
49 |
14 |
3 |
7 |
4 |
Варіант -31
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; B<D,G,E,F; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
18 |
15 |
8 |
10 |
9 |
16 |
11 |
17 |
10 |
4 |
7 |
9 |
10 |
10 |
8 |
14 |
8 |
22 |
16 |
28 |
4 |
14 |
18 |
12 |
8 |
10 |
12 |
20 |
8 |
8 |
10 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 15% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; I<H; D<K; C<E,D; F<I,J; G<H; A<G,F,K; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
5 |
10 |
5 |
8 |
8 |
12 |
m |
7 |
8 |
9 |
10 |
6 |
2 |
9 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Вартість С=80
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
20 |
17 |
9 |
22 |
20 |
26 |
10 |
Макс. трив. |
10 |
12 |
4 |
10 |
5 |
8 |
6 |
Варт. при макс. трив. |
8 |
10 |
4 |
14 |
8 |
12 |
4 |
Варіант -32
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,E,F; D<J; A<G; C<E,F; I<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
15 |
16 |
7 |
9 |
6 |
11 |
17 |
12 |
4 |
14 |
16 |
10 |
8 |
10 |
5 |
12 |
10 |
17 |
6 |
8 |
7 |
12 |
20 |
10 |
12 |
6 |
8 |
14 |
9 |
12 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F; C<E,D; F<E,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
8 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
9 |
12 |
6 |
2 |
9 |
4 |
7 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; E<G; A<D; C<D. Вартість на 10% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
4 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
25 |
21 |
10 |
Макс. трив. |
10 |
10 |
6 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
13 |
7 |
4 |
Варіант -33
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J,K; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
15 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
14 |
10 |
12 |
10 |
8 |
9 |
12 |
10 |
14 |
10 |
14 |
10 |
7 |
8 |
20 |
12 |
20 |
14 |
12 |
8 |
12 |
6 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
8 |
12 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; A<D; C<G,D. Вартість — середня між максимальною та мінімальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
15 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
9 |
Варіант -34
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку.Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
4 |
6 |
12 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
8 |
4 |
12 |
7 |
12 |
9 |
12 |
4 |
21 |
9 |
11 |
4 |
12 |
7 |
10 |
8 |
8 |
12 |
8 |
10 |
12 |
6 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
8 |
6 |
6 |
8 |
4 |
10 |
6 |
3 |
4 |
2 |
7 |
b |
12 |
12 |
9 |
14 |
10 |
14 |
10 |
5 |
9 |
8 |
7 |
m |
10 |
8 |
7 |
10 |
6 |
12 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Вартість С=60
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
12 |
16 |
9 |
22 |
15 |
16 |
10 |
Макс. трив. |
8 |
8 |
6 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
4 |
4 |
14 |
3 |
7 |
4 |
Варіант -35
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; A<G; C<E,F; G<H; E<J; B<D,G,E,F;
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
2 |
10 |
5 |
7 |
13 |
10 |
6 |
4 |
12 |
7 |
6 |
10 |
8 |
9 |
12 |
7 |
6 |
8 |
4 |
8 |
12 |
8 |
4 |
18 |
20 |
12 |
15 |
8 |
5 |
3 |
12 |
7 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10% більшою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
I<H; G<H; B<F,K; D<K; C<E,D; F<I,J; E<K; A<G,F,K.
Тривалості робіт зведені в таблицю - в першому рядку.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
12 |
7 |
12 |
8 |
4 |
18 |
8 |
9 |
8 |
12 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; F<G; B<C,E,F; C<D. Вартість — на 10% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
2 |
3 |
3 |
6 |
2 |
4 |
3 |
Варт. при мін. трив. |
16 |
24 |
9 |
22 |
15 |
21 |
10 |
Макс. трив. |
8 |
12 |
6 |
8 |
8 |
8 |
6 |
Варт. при макс. трив. |
4 |
17 |
4 |
14 |
3 |
7 |
4 |
Варіант -36
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: G<H; F<K; G<I; B<D,G,E,F; D<J; A<G; C<E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
10 |
6 |
5 |
8 |
7 |
9 |
10 |
11 |
17 |
12 |
4 |
6 |
10 |
5 |
11 |
7 |
9 |
16 |
8 |
8 |
10 |
6 |
13 |
4 |
10 |
8 |
10 |
4 |
8 |
12 |
16 |
6 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде рівною середньому її значенню, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
A<G,F,K; B<F,K; C<E,D; G<H; I<H; D<K; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
2 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
9 |
10 |
9 |
14 |
10 |
4 |
8 |
5 |
10 |
8 |
10 |
m |
6 |
9 |
6 |
10 |
6 |
2 |
6 |
4 |
6 |
4 |
8 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; D<G; A<D; C<D. Вартість С=70
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
2 |
4 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
12 |
15 |
21 |
10 |
Макс. трив. |
10 |
10 |
6 |
10 |
4 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
6 |
3 |
7 |
4 |
Варіант -37
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: A<G; F<K; G<I; D<J; C<E,F; G<H; B<D,G,E,F; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
3 |
8 |
5 |
16 |
9 |
9 |
6 |
10 |
9 |
12 |
14 |
8 |
4 |
12 |
8 |
12 |
5 |
10 |
10 |
7 |
6 |
7 |
4 |
12 |
5 |
12 |
6 |
8 |
9 |
12 |
4 |
12 |
12 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
9 |
9 |
9 |
10 |
8 |
4 |
10 |
5 |
9 |
8 |
10 |
m |
6 |
8 |
4 |
8 |
6 |
2 |
8 |
4 |
8 |
5 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: A<D; B<C,E,F; E<G; C<D. Вартість — на 10% більша від мінімальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
14 |
22 |
15 |
21 |
10 |
Макс. трив. |
12 |
9 |
6 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
49 |
14 |
3 |
7 |
4 |
Варіант -38
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: D<J; F<K; G<I; B<D,G,E,F; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
18 |
15 |
8 |
10 |
9 |
16 |
11 |
17 |
10 |
4 |
7 |
9 |
10 |
10 |
8 |
14 |
8 |
22 |
16 |
28 |
4 |
14 |
18 |
12 |
8 |
10 |
12 |
20 |
8 |
8 |
10 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 15% меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; I<H; D<K; C<E,D; F<I,J; G<H; A<G,F,K; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
5 |
10 |
5 |
8 |
8 |
12 |
m |
7 |
8 |
9 |
10 |
6 |
2 |
9 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; F<G; A<D; C<D. Вартість С=80
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
20 |
17 |
9 |
22 |
20 |
26 |
10 |
Макс. трив. |
10 |
12 |
4 |
10 |
5 |
8 |
6 |
Варт. при макс. трив. |
8 |
10 |
4 |
14 |
8 |
12 |
4 |
Варіант -39
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,E,F; D<J; A<G; C<E,F; I<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
15 |
16 |
7 |
9 |
6 |
11 |
17 |
12 |
4 |
14 |
16 |
10 |
8 |
10 |
5 |
12 |
10 |
17 |
6 |
8 |
7 |
12 |
20 |
10 |
12 |
6 |
8 |
14 |
9 |
12 |
4 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 5 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F; C<E,D; F<E,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
9 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
9 |
14 |
10 |
8 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
9 |
12 |
6 |
2 |
9 |
4 |
7 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; E<G; A<D; C<D. Вартість на 10% менша від максимальної.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
4 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
25 |
21 |
10 |
Макс. трив. |
10 |
10 |
6 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
13 |
7 |
4 |
Варіант -40
1. Побудувати мережу проекту, розрахувати параметри подій (ранні та пізні строки звершення, резерви часу), та робіт (ранні та пізні строки початку та закінчення робіт, повні, вільні, незалежні та ґарантовані резерви часу), визначити критичний шлях для заданого відношення передування та детермінованих тривалостей робіт за методом СPM, побудувати гістограми розподілу ресурсів 2-х видів.
Відношення передування: F<K; G<I; B<D,G,E,F; D<J,K; A<G; C<E,F; G<H; E<J.
Тривалості робіт зведені в таблицю - в першому рядку. Два останні рядки відображають необхідні витрати ресурсів 1-го та другого виду.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
14 |
8 |
15 |
16 |
17 |
9 |
6 |
11 |
17 |
12 |
14 |
10 |
12 |
10 |
8 |
9 |
12 |
10 |
14 |
10 |
14 |
10 |
7 |
8 |
20 |
12 |
20 |
14 |
12 |
8 |
12 |
6 |
8 |
2. Побудувати мережу проекту та визначити ймовірність того, що дійсна тривалість проекту буде на 10 одиниць меншою, ніж середнє її значення, використовуючи метод PERT. Задані відношення передування, песимістична - b, найімовірніша - m та оптимістична - a тривалості для кожної з робіт.
Відношення передування:
B<F,K; G<H; I<H; D<K; A<G,F,K; C<E,D; F<I,J; E<K.
Тривалості робіт зведені в таблицю.
Трив. |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
a |
4 |
6 |
3 |
8 |
4 |
1 |
6 |
3 |
4 |
2 |
7 |
b |
8 |
10 |
8 |
12 |
10 |
4 |
10 |
5 |
9 |
8 |
7 |
m |
6 |
8 |
4 |
10 |
6 |
2 |
8 |
4 |
6 |
4 |
7 |
3. Побудувати множину Парето-оптимальних розв’язків для задачі оптимізації проекту за критеріями тривалості та вартості. Для заданої вартості виконання проекту С визначити оптимальні тривалості всіх робіт.
Відношення передування: B<C,E,F; A<D; C<G,D. Вартість — середня між максимальною та мінімальною.
|
A |
B |
C |
D |
E |
F |
G |
Мін. трив. |
4 |
3 |
3 |
6 |
2 |
1 |
3 |
Варт. при мін. трив. |
16 |
17 |
9 |
22 |
15 |
21 |
15 |
Макс. трив. |
10 |
10 |
4 |
10 |
6 |
8 |
6 |
Варт. при макс. трив. |
4 |
10 |
4 |
14 |
3 |
7 |
9 |
