5. Обработка результатов измерений.
1. Рассчитать
полное давление рабочего тела в
подпоршневом объеме в характерных
точках:
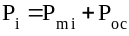 ,
,
где Pm
i [Па] -
манометрическое давление, снимаемое с
манометра;
Pос
[Па] -
атмосферное давление.
При расчетах
принимать следующие соотношения между
давлениями, измеренными в различных
системах единиц:
1 кг/см2
= 9.81*104
Па.
2. Определить
температуру газа в характерных точках
по показаниям милливольтметра. Для
хромель-копелевой термопары:
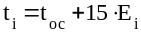 ,
,
где toc
- температура окружающей среды;
Еi
- термоЭДС термопары.
Рассчитать
абсолютную температуру окружающей
среды и газа в подпоршневом объеме:
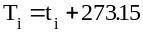 [К].
[К].
3. Рассчитать
случайную и приборную погрешности
измерения давления и температуры для
двух характерных точек.
4. Рассчитать
удельный объем воздуха до сжатия:
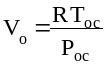 [м3/кг],
[м3/кг],
R = 287 Дж/кг*К - газовая
постоянная воздуха, и в характерных
точках процесса сжатия:
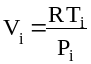 [м3/кг].
[м3/кг].
5. Вычислить
относительное давление
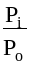 и относительный объем
и относительный объем
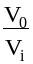 в характерных точках и их логарифмы
в характерных точках и их логарифмы
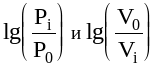 ,
принять
,
принять
 .
Построить график зависимости
.
Построить график зависимости
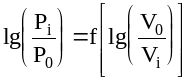 .
.
6. Определить
показатель политропы процесса сжатия
методом наименьших квадратов по формуле:
 ,
,
где
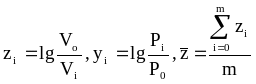 ,
,
m - число характерных
точек.
Результаты занести
в Таблицу 1.
Примечание:
обработку результатов производить с
четырьмя значащими цифрами, величину
показателя политропы округлить до
третьей значащей цифры.
1.Вопросы для контроля и проверки.
Что такое политропный
процесс? Чему равен показатель политропы?
Чему равен
показатель политропы для изобарного,
изохорного, изотермического и
адиабатического процессов?
Каковы особенности
обмена энергией для процессов сжатия
при n<1;
при 1<n<k;
при n>k.
Что такое метод
наименьших квадратов?
Как рассчитать
показатель политропы если известны
параметры в двух состояниях при его
протекании.


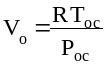 [м3/кг],
[м3/кг],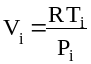 [м3/кг].
[м3/кг].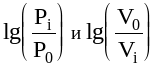 ,
принять
,
принять
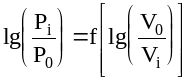 .
. ,
,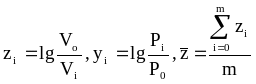 ,
,