8

БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ им. Д.Ф. Устинова

_______________________________________________________________

Кафедра К1

Лабораторная работа N 2

Определение соотношения теплоемкостей воздуха

по методу Клемана-Дезорма

Методические указания

	Составили:
	доц. Анискевич Ю.В.
	ассистент Мустейкис А.И.

Санкт-Петербург

1. Цель работы.

Целью работы является изучение газовых законов и определение отношения молярных теплоемкостей воздуха при постоянном давлении и постоянном объеме методом Клемана-Дезорма.

2. Краткая теория работы.

Всякий газ может находиться в различных состояниях, отличающихся параметрами состояния (давлением P, температурой T , объемом V , плотностью и т.д.). Уравнение, устанавливающее связь между давлением, объемом и температурой, называют уравнением состояния.

Для идеального газа уравнение состояния имеет вид:

, (1)

где – масса газа, M – масса одного моля газа, R – универсальная газовая постоянная.

Если при переходе некоторой массы газа из одного состояния в другое один из параметров остается постоянным, уравнение (1) имеет вид

PV = const (T = const – изотермический процесс),

= const (P = const – изобарный процесс),

= const (V = const – изохорный процесс).

При высоких давлениях (порядка десятков атмосфер) реальные газы не подчиняются уравнению (1), причины этого обусловлены наличием собственных размеров молекул и силами взаимодействия между ними, что и должно быть учтено в соответствующих уравнениях.

Из уравнений, предложенных для реальных газов, наиболее простым является уравнение Ван-дер-Ваальса. Для одного моля газа объемом оно имеет вид:

, (2)

где P – внешнее давление, оказываемое на газ; – внутреннее давление газа, появляющееся из-за сил притяжения между молекулами, b – поправка, учитывающая часть объема, занятого молекулами газа. При уменьшении плотности свойства всех реальных газов приближаются к свойствам идеального газа и уравнение (2) переходит в уравнение(1).

Запишем закон сохранения энергии (первое начало термодинамики):

, (3)

где dQ – количество тепла, подводимого к газу. Это тепло затрачивается на работу газа dA = PdV и на изменение его внутренней энергии dU .

Количество тепла, которое нужно подвести к газу (веществу) или отнять от него для изменения его температуры на один градус, называется теплоемкостью газа (вещества).

Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью .

Теплоемкость, отнесенная к одному молю вещества, называется молярной теплоемкостью C.

Удельная и молярная теплоемкости связаны выражением

. (4)

Величина теплоемкости зависит от условий, при которых происходит нагревание тела.

Пусть один моль газа нагревается при постоянном давлении (P = const , изобарный процесс). В этом случае получаемое газом тепло идет на увеличение его внутренней энергии и на совершение газом работы.

Если один моль газа нагревается при постоянном объеме (V = const – изохорный процесс), то для нагревания его на один градус требуется меньшее количество тепла, так как работа газом не совершается.

Между молярными теплоемкостями при постоянном давлении и постоянном объеме существует следующее соотношение:

. (5)

Отношение ( – показатель адиабаты) зависит только от числа степеней свободы i молекулы газа.

Число степеней свободы определяется числом атомов в молекуле и характером связи между ними. Для одноатомного газа i = 3, для двухатомного газа с жесткой связью i = 5 (с упругой связью i = 7), для трех и более атомов (нелинейная молекула, жесткая связь) i = 6.

На каждую степень свободы молекулы (согласно закону равнораспределения энергии по степеням свободы) приходится энергия, равная (Здесь k – постоянная Больцмана.)

Отношение также можно выразить через число степеней свободы молекулы:

. (6)

Формула (6) справедлива и для отношения удельных теплоемкостей.

Величина γ входит в уравнение Пуассона

= const, (7)

описывающего адиабатный процесс в газах.

Адиабатным процессом называется процесс, протекающий без теплообмена с окружающей средой. Если процесс протекает достаточно быстро (например, при быстром расширении или сжатии газа), то его можно считать практически адиабатным и при отсутствии тепловой изоляции.

Метод Клемана-Дезорма.

Пусть мы имеем баллон с газом, находящийся при атмосферном давлении и комнатной температуре . Накачаем в баллон воздух до некоторого давления , . Через некоторое время (1-2 мин.) вследствие теплообмена с окружающей средой температура в баллоне станет комнатной . Единица массы газа при этом занимает объем . Это состояние соответствует точке 1 (см. рис.1). Параметры данного состояния , , .

Откроем на короткое время (до 2 с) кран, соединяющий баллон с атмосферой. При этом воздух, находящийся в баллоне, быстро (адиабатически) расширится и вследствие этого охладится до температуры , а давление будет равно атмосферному . Единица массы газа займет объем . Это состояние соответствует точке 2 (см. рис.2). Параметры данного состояния , , .

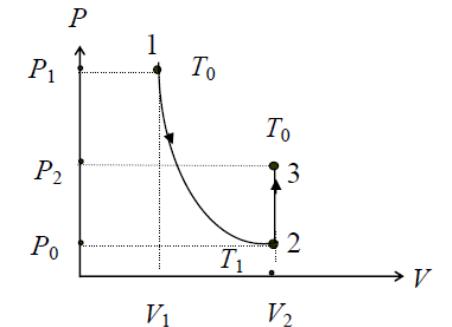
Рис.2 Графики процессов: 1-2 – адиабата; 2-3 – изохора.

Как только кран температура (вследствие теплообмена) начинает повышаться до комнатной и (так как процесс изохорный) давление также повышается до , . Это состояние соответствует точке 3 (см. рис.2). Параметры данного состояния , , .

Получим расчетную формулу для в нашей работе.

Переход из состояния 1 в состояние 2 описывается уравнением Пуассона. Для состояний 1 и 2 запишем уравнение адиабатического процесса:

. (8)

Переход из состояния 2 в состояние 3 – изохорный. Поэтому параметры состояний 2 и 3 связаны следующим соотношением:

. (9)

Возведем уравнение (9) в степень , получим:

. (10)

Приравняем правую часть последнего уравнения к правой части уравнения (8):

. (11)

Подставим в (11) и . Получим:

. (12)

При условии, что и много меньше обе части уравнения можно разложить в ряд следующим образом:

или

Отсюда получим расчетную формулу для :

.