Практичне заняття № 10

Тема: Функції та графіки.

Мета: Оволодіння узагальненими методами дослідження функцій.

Теоретичний блок:

1. Різні означення функції.

2. Властивості функції а) область визначення функції; б) множина значень функції; в) парність та непарність функції; г) періодичність функції.

Практичний блок:

1. Знайти область визначення функцій:

1. 

2. 

3. 

4. 

5. 

6. 

2. Знайти множину значень функцій:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

3. Дослідити функції на парність:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

4. Знайти періоди функції:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

5. Чи являються функції періодичними?

1. 

2. 

3. 

4. 

Практичне заняття № 11

Тема: Функції та графіки.

Мета: Оволодіння узагальненими методами дослідження функцій.

Теоретичний блок:

1. Монотонність функції.

2. Алгоритм знаходження проміжків монотонності функції елементарними методами.

Практичний блок:

1. Знайти інтервали монотонності функцій (використовуючи визначення):

1. y=x;

2. y=x²;

3. y=x³;

4. y=x⁴;

5. 

6. 

7. y=6x²-24x+1;

8. y=x²-2x;

9. y=-3x²+9x-7;

10. y=x³-3x;

11. y=lg x;

12. y=log_0,3(-x);

13. y=(0,7)^2x-1;

14. 

15. 

2. Визначте інтервали монотонності:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Практичне заняття № 12

Тема: Функції та графіки.

Мета: Оволодіння узагальненими методами дослідження функцій.

Теоретичний блок:

1. Екстремуми функції.

2. Найбільше та найменше значення функції.

3. Визначення напрямів опуклості графіка функції

Практичний блок:

1. Знайти екстремум функції:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

2. Знайти найбільше (найменше) значення функції на інтервалі:

   1. 

   2. 

   3. 

   4. 

   5. 

   6. 

   7. 

3. Дослідити опуклість функції:

   1. 

   2. 

   3. 

   4. 

   5. 

   6. 

   7. 

   8. 

   9. 

Практичне заняття № 13

Тема: Функції та графіки.

Мета: Оволодіння узагальненими методами побудови графіків функцій.

Теоретичний блок:

1. Елементарні перетворення графіків функцій.

2. Побудова графіків складених функцій.

Практичний блок:

1. Побудуйте графіки функцій:

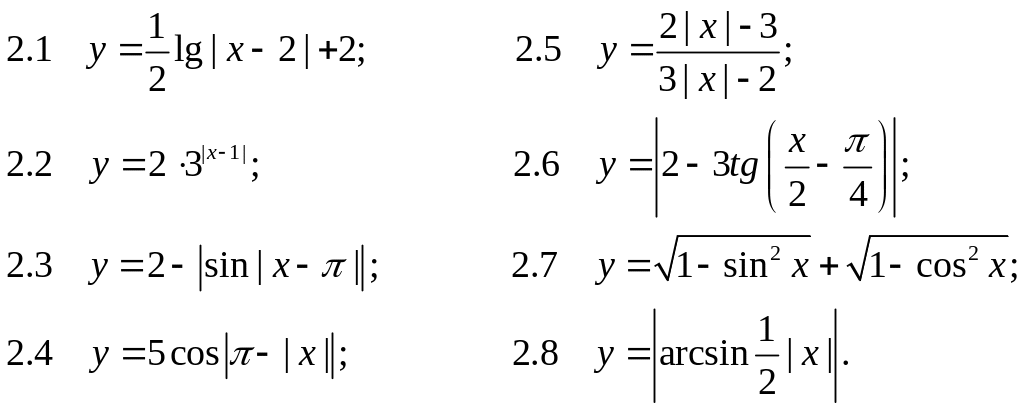
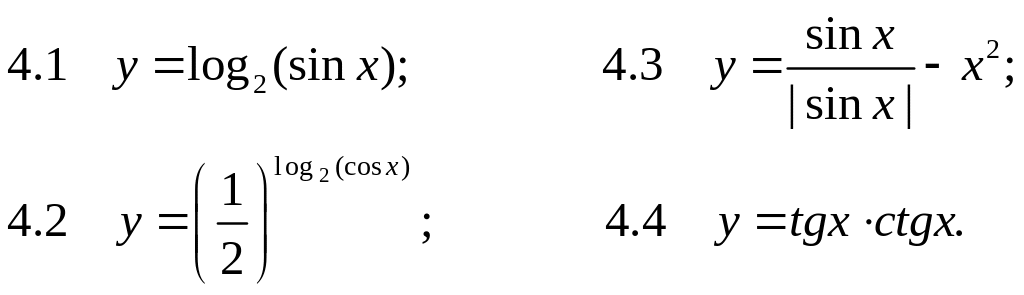
Практичне заняття № 14

Тема: Функції та графіки.

Мета: Оволодіння узагальненими методами побудови графіків функцій.

Теоретичний блок:

1. Елементарні перетворення графіків функцій.

2. Побудова графіків складених функцій.

Практичний блок:

1. Дослідіть функцію та побудуйте її графік:

1. 

2. 

3. 

4. 

5. 

6. 

2. Побудуйте графіки функцій (виконавши необхідні перетворення та пояснення).

   1. 

   2. 

   3. 

   5. 

   6. 

3. Побудуйте графіки функцій:

3.1

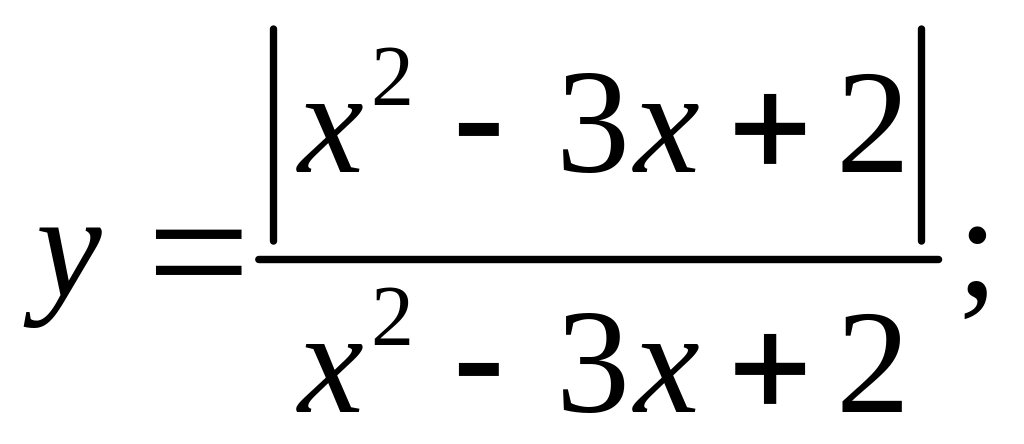
3.2

3.3

3.4

3.5

Практичне заняття № 15-16

Тема: Лінійна та квадратична функція. Лінійні та квадратичні рівняння та нерівності. Лінійні та квадратичні рівняння і нерівності з параметрами.

Мета: Оволодіння узагальненими методами розв’язання лінійних та квадратичних рівнянь і нерівностей з параметрами.

Теоретичний блок:

1. Квадратний тричлен. Лінійні та квадратні рівняння і нерівності.

2. Лінійні та квадратні рівняння і нерівності з параметрами.

Практичний блок:

1. Виділіть повний квадрат:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

2. Розв’язати рівняння:

1. 7х²+20х+14=0;

2. 9х²+78х+25=0;

3. х²+14х-1=0;

4. 2х²-9х+10=0.

3. Що можна сказати про корені квадратичного рівняння?

1. 2х²+х-3=0;

2. ах²-2х-3=0.

4. Виразіть залежність між коефіцієнтами рівняння х²+рх+q=0, якщо один з коренів рівний –1.

5. В рівнянні х²+рх-35=0 один з коренів рівний 7. Знайдіть другий корінь та коефіцієнт р.

6. Різниця коренів рівняння х²+рх-26=0 рівна 15. Знайдіть р.

7. Нехай х₁ та х₂ – корені рівняння х²-3х-5=0. Не розв’язуючи рівняння знайдіть:

8. Знайти корені рівняння, використовуючи теорему обернену теоремі Вієта.

1. х²+4х-21=0;

2. х²+5х+6=0;

3. х²-7х+10=0;

4. х²-100х+99=0;

5. х²-77х-78=0;

6. 2х²+х-1=0;

7. 3х²-2х-1=0;

8. 2х²-3х-2=0;

9. 3х²-7х+4=0

9. Розв’яжіть рівняння

; ; ;

9. Розв’яжіть нерівність:

   1. 

   2. 

   3. 

   4. 

   5. 

   6. 

9. Розв’яжіть нерівність

1. х²+4х-21>0;

2. х²+4х-21<0;

3. -3х²+2х-1<0;

4. -3х²+2х-1>0;

5. х²+5х+6>0;

6. х²+5х+6£0

11. Розв’яжіть рівняння (а - параметр):

1. х²-2ах+4а=0;

2. ах²+(а-2)х-8=0;

3. ах²-(а-4)х-а+4=0.

11. При яких значеннях а корені рівняння х²-2ах+а²-1=0 будуть знаходиться між числами –2 та 4?

11. Запишіть умови, при яких рівняння |a-2| х²-3|a+2|+6a=0 має:

1. два різних корені;

2. корені різних знаків;

3. два відмінних кореня;

4. два додатних кореня

14. Розв’яжіть нерівність:

1. х²-2ах+4a<0;

2. ах²+(а-2)х-8³0;

3. ах²-3ах+2а-1<0.

4. 2a(a-2)x=a-2;

5. а²+ах<1-x;

6. ах²-2х+4>0.

15. Знайти а, при яких:

    1. нерівність правильна для всіх |х|<1;

    2. з нерівності слідує нерівність