Розв’язати нерівність методом інтервалів:
+2
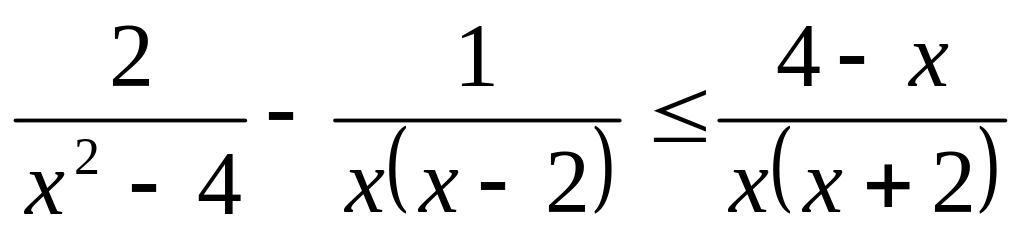
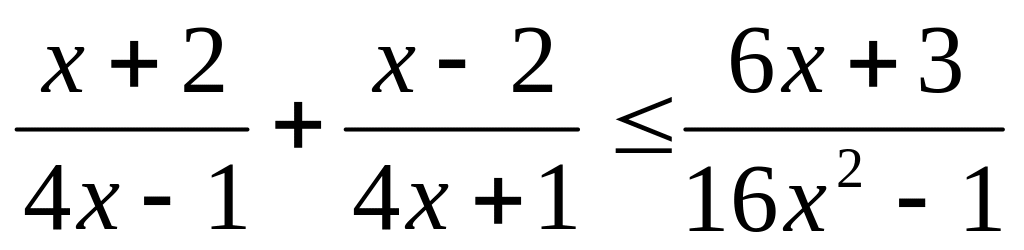
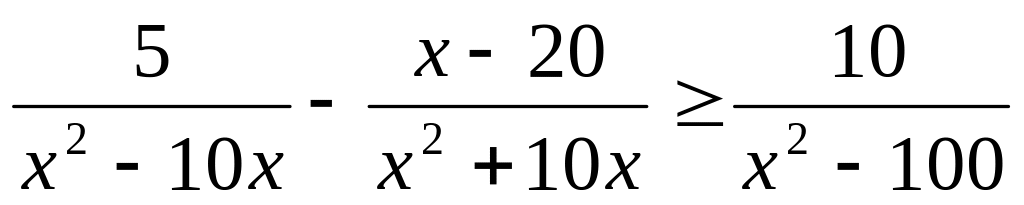
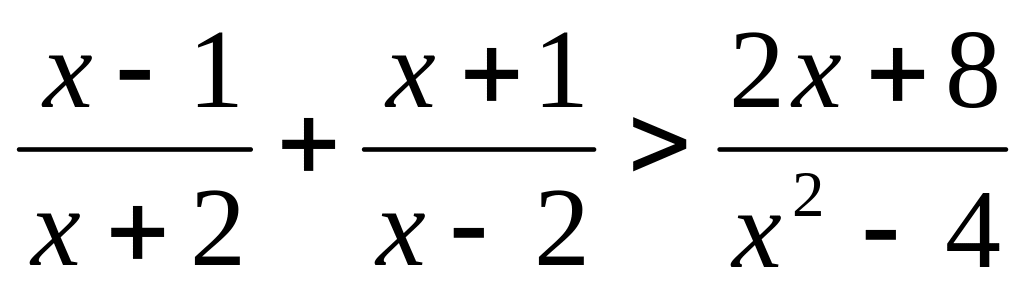
Індивідуальне завдання №5 «Ірраціональні рівняння та нерівності»
Розв’язати ірраціональні рівняння:
;
;
;
;
;
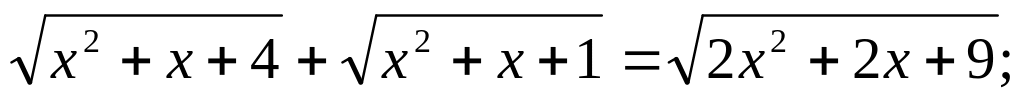
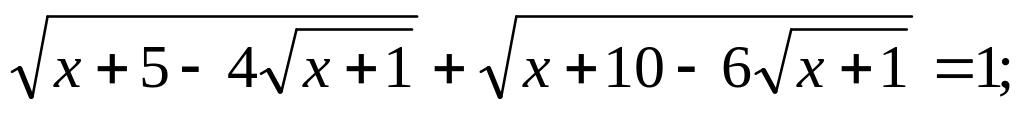
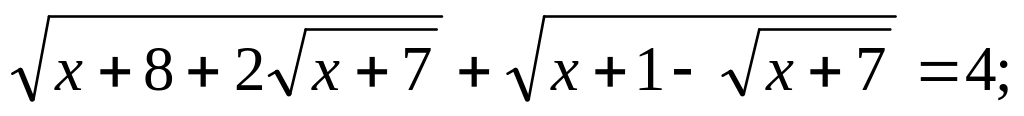
Розв’язати ірраціональну нерівність:
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
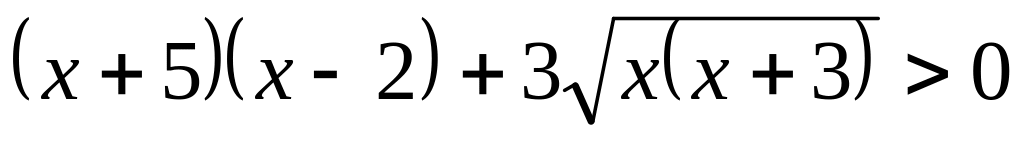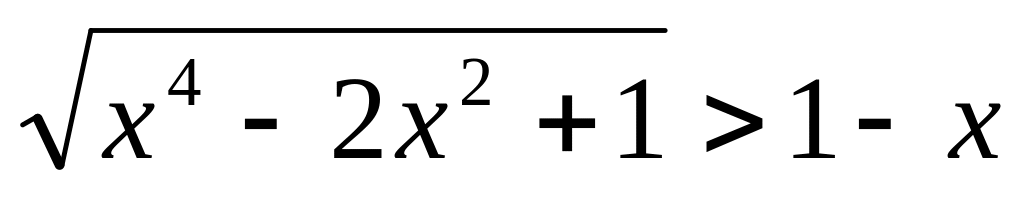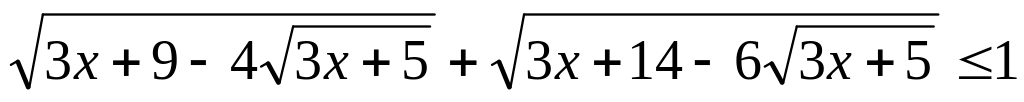Результати роботи студента над індивідуальними завданнями оцінюються наступним чином:
Індивідуальне завдання |
Кількість балів |
Індивідуальне завдання №1 |
4 |
Індивідуальне завдання №2 |
4 |
Індивідуальне завдання №3 |
6 |
Індивідуальне завдання №4 |
6 |
Індивідуальне завдання №5 |
6 |
Завдання до заліку
Записати символічно висловлення, використовуючи квантори: а) деякі натуральні числа діляться на 2 та 7; б) хоча б одне з чисел 11, 18, 12 ділиться на 2. Визначити та обґрунтувати істинність чи хибність речення. Побудувати заперечення цього висловлення та також визначити його істинність.
Які слова: «Достатньо», «Необхідно», або «Необхідно та достатньо» потрібно поставити в наступних висловленнях, щоб одержати істинне висловлення:
а) щоб вступити в педуніверситет, … мати середню освіту;
б) щоб чотирикутник був квадратом, … щоб всі його сторони були рівні;
в) щоб периметр квадрата був рівний 20см, … щоб його сторона була рівна 5см;
г) щоб сума двох чисел була числом парним, … щоб кожна складова була парним числом;
д) щоб корені рівняння x2+px+q були додатними, … щоб p < 0 та q > 0;
Довести рівності: а) ; б) A\(BÇC)=(A\B) È (A\C).
Довести, що .
Парне число а при діленні на 3 дає остачу 1. Чому дорівнює остача від ділення числа а на 6?
Спростити:
Довести ірраціональність чисел:
16 туристів розділились на дві рівні трупи для пошуку товариша, який загубився. Серед них тільки 4 тих, хто добре знайомий с місцевістю. Яким числом способів вони можуть розділитись так, щоб в кожну групу увійшло 2 туристи, що знають місцевість.
Знайти член розкладу бінома , що не містить а.
Знайти множину значень функції
Дослідити функцію на парність
Знайти період функції
Знайти інтервали монотонності функції y=6x2–24x+1 (використовуючи визначення).
Знайти екстремум функції
Знайти найбільше (найменше) значення функції на інтервалі: .
Дослідити опуклість функції .
Побудувати графіки функцій:
Дослідити функцію та побудувати її графік
Розв’язати рівняння .
Розв’язати нерівність: х2–2ах+ 4a < 0;
Знайти а, при яких нерівність правильна для всіх |х|<1.
Представити у вигляді суми чи різниці цілого виразу та дробу:
Представити правильний дріб у вигляді суми найпростіших:
Розв’язати нерівність
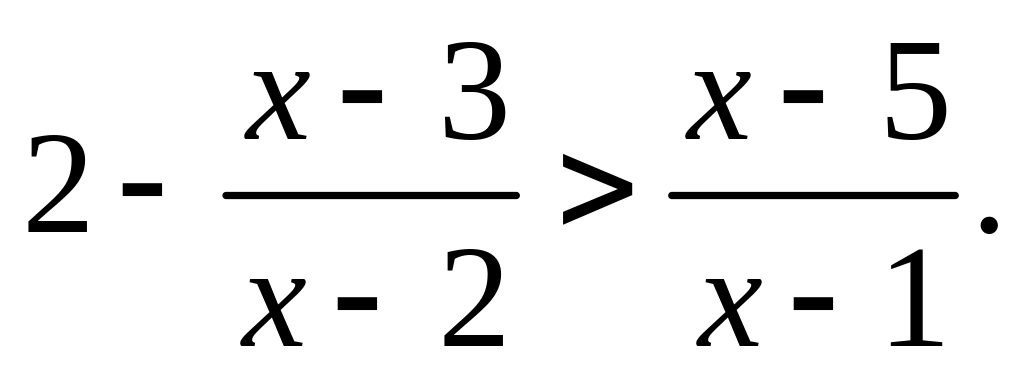
Довести, що рівняння не має дійсних коренів:
.Розв’язати рівняння
.Розв’язати рівняння
.Довести, що нерівність не має розв’язків
.Розв’язати нерівність
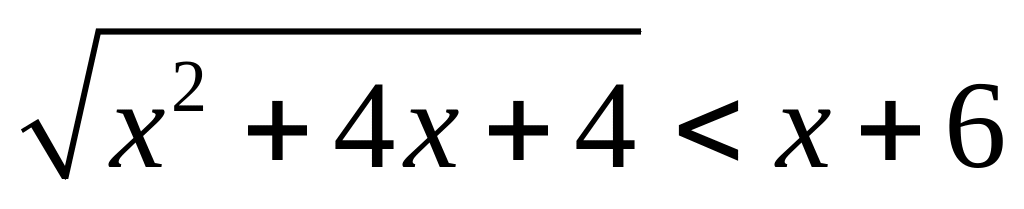.Розв’язати систему нерівностей
.
Методи навчання: створення проблемних ситуацій, складання узагальнюючих таблиць та графічних схем
Методи контролю : оцінювання результатів виконання контрольних робіт, індивідуальних завдань, проведення тестування, перевірка виконання домашніх завдань, залік.