
- •Вопрос 1. Назовите некоторые основные проблемы эконометрического моделирования.
- •Некоторые проблемы эконометрического моделирования
- •Вопрос 2. Как называется метод, который наиболее часто используется при оценке параметров линейной модели в эконометрике?
- •Вопрос 3. Как называются показатели, которые характеризует степень разброса случайной величины вокруг ее среднего значения?
- •Вопрос 5. Что обозначает и как рассчитывается функция эластичности в линейной эконометрической модели ?
- •Вопрос 6. Что мы подразумеваем под свойствами линейной модели , если считаем, что ошибки - случайные величины?
- •Вопрос 7. В каких пределах будет заключена случайная ошибка с вероятностью 0.95, если она имеет Гауссовское распределение с параметром ?
- •Вопрос 8. При каких значениях статистики Фишера нулевая гипотеза отвергается, и какова вероятность того, что мы отвергнем верную гипотезу?
- •Вопрос 9. Какая из трех нулевых гипотезе , , является простой, а какая – сложной?.
- •Вопрос 10. Что такое гетероскедастичность и автокоррелированность ошибок?
Вопрос 5. Что обозначает и как рассчитывается функция эластичности в линейной эконометрической модели ?
Ответ
В модели функция эластичности имеет вид

и
при
 возрастает от
до
с возрастанием значений
возрастает от
до
с возрастанием значений
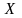 от
до
от
до
 .
Если
.
Если
 ,
то
,
то
 .
При
.
При
 функция
эластичности
функция
эластичности
 убывает
от
убывает
от
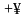 до
,
когда
изменяется от
до
,
когда
изменяется от
 до
.
до
.
К линейной форме связи можно привести и некоторые другие виды зависимости, характерные для экономических моделей.
Вопрос 6. Что мы подразумеваем под свойствами линейной модели , если считаем, что ошибки - случайные величины?
Ответ
Базовая, и наиболее простая модель для последовательности предполагает, что — независимые случайные величины, имеющие одинаковое распределение (i. i. d. — independent, identically distributed random variables).
Для
нас (пока!)
достаточно представлять случайную
величину
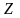 как
переменную величину,
такую, что до
наблюдения ее значения невозможно
предсказать это значение абсолютно
точно,
и, в то же время, для
любого
как
переменную величину,
такую, что до
наблюдения ее значения невозможно
предсказать это значение абсолютно
точно,
и, в то же время, для
любого
 ,
,
 ,
определена вероятность
,
определена вероятность

того,
что наблюдаемое
значение
переменной
не
превзойдет
;
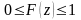 .
Функция
.
Функция
 ,
называется функцией
распределения
случайной
величины
(c.
d. f. — cumulative
distribution function).
,
называется функцией
распределения
случайной
величины
(c.
d. f. — cumulative
distribution function).
Говоря об ошибках как о случайных величинах, мы, Соответственно, понимаем указанную линейную модель наблюдений таким образом, что
а) существует (теоретическая, объективная или в виде тенденции) линейная зависимость значений переменной от значений переменной с вполне определенными, хотя обычно и не известными исследователю, значениями параметров и ;
б)
эта линейная связь для реальных
статистических данных не
является строгой:
наблюдаемые значения
переменной
отклоняются
от значений
 ,
указываемых моделью линейной связи
,
указываемых моделью линейной связи

в) при заданных (известных) значениях конкретные значения отклонений

не могут быть точно предсказаны до наблюдения значений даже если значения параметров и известны точно;
г)
для каждого
 ,
определена вероятность
,
определена вероятность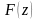 того,
что наблюдаемое
значение
отклонения
не
превзойдет
,
причем эта вероятность не
зависит от номера наблюдения;
того,
что наблюдаемое
значение
отклонения
не
превзойдет
,
причем эта вероятность не
зависит от номера наблюдения;
д)
вероятность того, что наблюдаемое
значение отклонения
в i-м
наблюдении
не
превзойдет
,
не
зависит
от того, какие именно значения принимают
отклонения в остальных
 наблюдениях.
наблюдениях.
Вопрос 7. В каких пределах будет заключена случайная ошибка с вероятностью 0.95, если она имеет Гауссовское распределение с параметром ?
Ответ
Итак, предположив, что в модели наблюдений
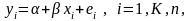
ошибки
 — независимые
случайные величины, имеющие одинаковое
распределение (i.
i. d),
мы
должны сделать и предположение о том,
каким
именно
является это
распределение.
— независимые
случайные величины, имеющие одинаковое
распределение (i.
i. d),
мы
должны сделать и предположение о том,
каким
именно
является это
распределение.
Классические методы статистического анализа линейных моделей наблюдений предполагают, что таковым является распределение Гаусса (Gaussian distribution), функция плотности которого имеет вид

График указанной функции плотности имеет колоколообразную форму
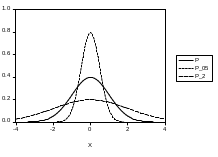
Параметр
 характеризует степень рассредоточения
распределения вдоль оси абсцисс. На
диаграмме представлены графики функций
плотности гауссовского распределения
при трех различных значениях параметра
характеризует степень рассредоточения
распределения вдоль оси абсцисс. На
диаграмме представлены графики функций
плотности гауссовского распределения
при трех различных значениях параметра .
Из трех представленных функций наибольшее
значение в нуле имеет функция плотности
с
.
Из трех представленных функций наибольшее
значение в нуле имеет функция плотности
с
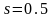 ,
наименьшее — функция плотности с
,
наименьшее — функция плотности с
 ,
а промежуточное между ними — функция
плотности с
,
а промежуточное между ними — функция
плотности с
 .
Эти значения равны, Соответственно,
.
Эти значения равны, Соответственно,

Гауссовское
распределение симметрично
относительно нуля,
и это предполагает, что положительные
ошибки столь же вероятны, как и
отрицательные;
при этом,
малые ошибки встречаются чаще, чем
большие.
Если случайная ошибка имеет гауссовское
распределение с параметром
,
то с
вероятностью
 ее
значение будет заключено в пределах от
ее
значение будет заключено в пределах от
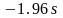 до
до
 .
Соответственно, для трех рассмотренных
случаев получаем: с вероятностью
значение случайной ошибки заключено в
интервале
.
Соответственно, для трех рассмотренных
случаев получаем: с вероятностью
значение случайной ошибки заключено в
интервале
 —
при
,
—
при
,
 -
при
,
-
при
,
 -
при
.
-
при
.
Хотя гауссовское распределение довольно часто вполне приемлемо для описания случайных ошибок в моделях наблюдений, оно вовсе не является универсальным. Такое распределение характерно для ситуаций, когда результирующая ошибка является следствием сложения большого количества независимых случайных ошибок, каждая из которых достаточно мала.
