Найчастіше в статистистико-економічних дослідженнях

α = 0,05 або α = 0,01.

Таблиця 4

Критичні значення кореляційного відношення і коефіцієнта детермінації для α = 0,05.

	1	2	3	4	5	6	8	10	20
16	0,219	312	378	429	477	507	564	609	740
17	208	297	361	411	452	488	545	590	724
18	197	283	345	394	435	470	527	573	709
19	187	270	331	379	419	454	510	556	694
20	179	259	318	364	404	432	495	540	680

Розподіл в цих таблицях залежить від числа ступенів вільності міжгрупової ( ) і середньої з групових ( ) дисперсій. В аналітичному групуванні вони обчислюються так :

= m – 1; = n – m,

де n, m –відповідно кількість елементів сукупності та кількість груп. У нашому прикладі 20 господарств і 3 групи, отже

= 3 – 1 =2 ; = 20 – 3 = 17

Для рівня істотності = 0,05 при цих ступенях вільності

Тобто, при відсутності зв’язку між ознаками тільки у 5 випадках із 100 перевищить 0,30. У нашому прикладі = 0,746 більше від критичного 0,297, що свідчить про істотність кореляційного зв’язку між продуктивністю праці та урожайністю.

Для перевірки істотності зв”язку використовують функціонально зв”язану з характеристику F–критеріїв (крітерії Фішера), які обчислюються за формулами

або .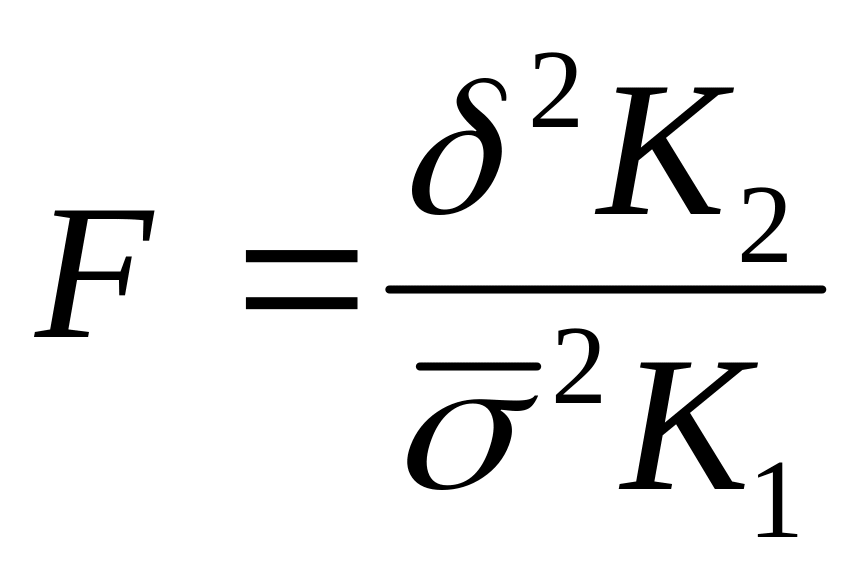

Існують таблиці критичних значень F-критерію. Перевірку істотності з його допомогою здійснюють аналогічно описаній вище для кореляційного відношення .

У нашому прикладі , що значно більше від критичного F_0,95( 2,17) = 3,59. Це свідчить про істотність кореляційного зв’язку між ознаками, які вивчають.

Комбінаційні аналітичні групування використовують для аналізу зв’язку результативної ознаки з двома і більше факторними ознаками від кожного з факторів при фіксованих значеннях інших. Методи вимірювання такого типу зв’язку та перевірки його істотності називають багатофакторними комплексами. Розрахунки тут громіздкі і потребують ЕОМ.

8.3. Основи кореляційно- регресійного аналізу.

У кореляційно-регресійному аналізі оцінка лінії регресії здійснюється не в окремих точках, як в методі аналітичного групування, а в кожній точці інтервалу зміни факторної ознаки х. Тобто лінія регресії у данім випадку безперервна і зображується у вигляді певної функції , яка називається рівнянням регресії, а – це теоретичні значення результативної ознаки.

І етап. Теоретичне обгрунтовання моделі.

Розглянемо парну (тобто з однією факторною ознакою ) модель.

При виборі ії функціонального виду використовуються графіки, аналітичні групування та теоретичного обгрунтування.

При невеликому обсязі сукупності доцільно будувати графіки у вигляді кореляційного поля, де кожному елементу відповідає точка, а всі елементи утворюють скупчення точок. Загальний вигляд кореляційного поля дозволяє зробити висновок щодо форми лінії регресії.

При великому обсязі користуються методом аналітичного групування. Графік групових середніх є емпіричною лінією регресії.

Можливий перебір функцій. Обчислюють рівняння регресії різних видів, із них вибирають найкраще. Як правило, це рівняння з найвищим коефіцієнтом тісноти зв’язку між ознаками, що вивчають.

Серед безлічі функцій в статистико-економічному аналізі найпоширенішою є лінійна . Це пояснюється ії простотою та змістовністю параметрів. Крім того, факторна ознака варіює в невеликих межах, що дає змогу показати апроксимацію (наближення кривої до ламаної) зв’язку лінійною функцією.

Параметр називають коефіцієнтом регресії. Він показує, на скільки одиниць власного виміру в середньому змінюється значення ознаки у зі збільшенням значення ознаки х на одиницю її власного розміру.

Параметр - це значення у при х=0. Якщо х не може приймати нульових значень, то економічно не інтерпретується і як вільний член рівняння має тільки розрахункове значення.

Побудований за даними табл. 1 графік кореляційного поля має вигляд лінійної функції.

Розміщення точок на графіку свідчить про можливість використання лінійного рівняння .

ІІ етап. Оцінка лінії регресії. Оцінками лінії регресії є теоретичні значення результативної ознаки у.

Визначають параметри обраного рівняння з допомогою метода нейменших квадратів. Основна умова методу полягає в мінімізації суми квадратів відхилень емпіричних значень у від теоретичних , тобто

.

Ц е дає можливість отримати найкращі оцінки параметрів і . Для їх отримання складають і розв”язують систему нормальних рівнянь. Лінійній моделі відповідає система рівнянь з двома невідомими.

;

.

У нашому прикладі:

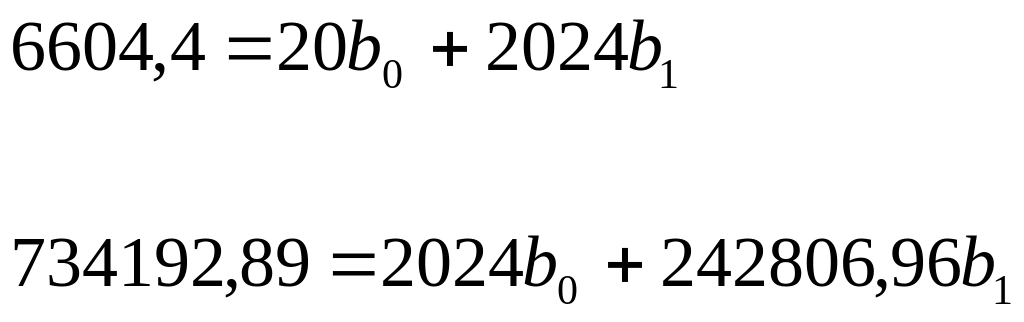
Помножимо 1-е рівняння на 101,2= і віднімемо друге рівняння від першого.

Лінійне рівняння регресійного зв’язку між продуктивністю праці та урожайністю має такий вигляд:

У = 154,84+1,733х.

Таким чином, при збільшенні урожайності на 1ц/га продуктивність праці зростає у середньому на 1,733 ц/особу. Цей коефіцієнт регресії близький до обчислюваних раніше ефектів моделі анал.групування (2,13 і 1,36 ц/особу)

Для дослідження форми зв’язку можуть бути використані й нелінійні рівняння регресії різних видів. У цьому разі при визначенні параметрів методом найменших квадратів рівняння регресії слід привести до лінійного вигляду шляхом певних перетворень.