ТЕОРИЯ ОШИБОК

Окружающий нас физический мир состоит из материи, которую мы наблюдаем в твердом, жидком, газообразном и плазменном состояниях вещества, в виде физических полей, вакуума и открытых недавно астрофизиками темной материи и темной энергии. Вся материя упорядочена и поэтому обладает формой или иначе информацией. При экспериментальном изучении материальных объектов и физических процессов (движения материи в широком смысле) мы получаем часть содержащейся в них информации, характеризуя ее с помощью определенной системы мер. Используя таким образом понятия материи, информации и меры, мы накапливаем наши знания о мире в виде качественных и количественных характеристик материи, включая универсальные (мировые) константы.

Основным методом исследований в физике является опыт. В ходе опытов выявляются физические законы – устойчивые, повторяющиеся объективные закономерности движения материи. Например, механика – это часть физики, изучающая закономерности механического движения и причины, определяющие это движение. Молекулярная физика изучает строение и свойства вещества, исходя из его молекулярного строения. В свою очередь, термодинамика изучает свойства макроскопических систем взаимодействующих тел (молекул, атомов) в состоянии термодинамического равновесия и процессы перехода между такими состояниями. Физические законы и закономерности отражают взаимосвязь различных физических величин. Для характеристики последних используются соответствующие эталонные единицы измерения, например, международная система единиц СИ:

Метр (м) – длина пути света в вакууме за 1/299792458 с;

Килограмм (кг) – масса платиноиридиевого цилиндра в Международном бюро мер и весов под Парижем;

Секунда (с) – время, равное 9192631770 периодам излучения, соответствующему переходу между двумя сверхтонкими уровнями основного состояния Цезия-133;

Ампер (А) – сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого диаметра, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2∙10^-7 Н;

Кельвин (К) – 1/273,16 часть термодинамической температуры тройной точки воды;

Моль (моль) – количество вещества, содержащее столько же структурных элементов, сколько атомов содержится в углероде-12 массой 0,012 кг;

Кандела (кд) – сила света от монохроматического источника с частотой 540∙10¹² Гц и энергетической силой 1/683 Вт/ср;

Радиан (рад) – угол между двумя радиусами окружности, длина дуги между которыми равна радиусу;

Стерадиан (ср) – телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.

С помощью указанных семи основных и двух дополнительных (радиан и стерадиан) единиц измерений строятся производные единицы для различных физических величин. Размерностью физической величины является ее выражение в основных единицах. Например, размерность силы составит dim F = кг∙м/с².

Состояние термодинамических систем характеризуется совокупностью определенных физических величин, называемых термодинамическими параметрами. К основным термодинамическим параметрам относятся:

Температура – характеризует состояние термодинамического равновесия системы. Для ее измерения используются две шкалы: термодинамическая (в Кельвинах, K) и международная стоградусная шкала (в градусах Цельсия, ºС; значение 0 ºС отвечает температуре плавления льда и 100 ºС – температуре кипения воды при нормальном давлении 1,01325∙10⁵ Па). Связь между шкалами имеет вид Т К = Т ºС+273,16 ºС. Т = 0 К называется абсолютным нулем температуры;

Удельный объем – объем υ единицы массы

υ = V/m = 1/ρ,

где V – общий объем, m – общая масса, ρ – плотность тела;

Давление – сила, действующая со стороны тела на единицу площади перпендикулярно к ней

p = F/S,

где F – сила, S – площадь действия силы.

Давление измеряется в Паскалях (Па):

1 Паскаль = давление, создаваемое силой 1 Ньютон (Н), равномерно распределенной по площади 1 м². При этом 1 Па = 1 Н/м².

В настоящем пособии приводятся лабораторные работы по двум разделам: «Механика» и «Молекулярная физика и термодинамика». При подготовке второго раздела использованы разработки Российского научно-производственного объединения «Росучприбор».

1 Обработка результатов измерений

1.1 Виды измерений и статистическое распределение получаемых результатов

Измерить какую-либо величину – значит узнать, сколько в ней содержится соответствующих эталонных единиц. Измерить физическую величину абсолютно точно невозможно, так как всякое измерение сопровождается большей или меньшей ошибкой, называемой погрешностью.

Грамотно провести измерение – значит не только определить значение интересующей нас величины, но и оценить допущенную при этом погрешность и указать надежность (доверительную вероятность) найденных значений физической величины.

Измерения любых величин делятся на два вида: прямые и косвенные. Прямые измерения – такие, при которых искомая величина (x) считывается непосредственно по прибору. Косвенные измерения – когда измеряются другие величины (х_i), а интересующая нас величина (y) вычисляется по формуле, связывающей y и x_i определенной функциональной зависимостью. Методы определения ошибок того и другого видов измерений существенно различны.

Рассмотрим статистическое распределение результатов измерений.

Пусть производится измерение расстояния, пройденного телом (равномерно движущимся по горизонтальной плоскости металлическим шариком) за время t. Измерения проводятся с помощью фотоаппарата, затвор которого срабатывает через t секунд после выключения электромагнита с освобождением толкающей шарик сжатой пружины. Каждое измерение с номером i (i = 1, 2, 3 ...) дает значение пройденного расстояния x_i . Пусть проведено n измерений. Разобьем ось x на отрезки длиной Δx и посчитаем какое количество n_x измеренных значений x_i попадает в каждый из выбранных отрезков, то есть сколько раз измеренные значения были заключены между x и (x+Δx).

Вычислив отношение = n_x /n, мы получим относительное число измерений, попадающих в данный отрезок или, иначе, вероятность того, что x_i имеет значение, заключенное между x и (x+Δx). Значения мы будем изображать (рисунок 1.1) в виде прямоугольников с основанием от x до (x+Δx) и высотой . Полученный ступенчатый Δx многоугольник называется гистограммой статистического распределения результатов измерений.

Пусть, например, проведено 100 измерений (n = 100). Разобьем ось X на отрезки длиной 1 см (Δx = 1см). При подсчете оказалось, что значения от 92 см до 93 см имели 4 измерения (n₉₂ = 4), значения от 101 см до 102 см имели 17 измерений (n₁₀₁ = 17) и т.д. Тогда, соответственно,

и .

П родолжая вычисления, мы придем к гистограмме, изображенной на рисунке 1.1.

Если число проведенных опытов увеличивать до бесконечности (n→ ∞), а отрезки, на которые разбивается ось x, бесконечно уменьшать (Δx→ 0), то верхние основания прямоугольников составят плавную кривую плотности вероятности распределения результатов измерений .

Если действует только одна причина, вызывавшая разброс измеряемых значений, то вид , вообще говоря, может быть произвольным. В нашем случае, до момента отрыва шарика от пружины, действует множество различных причин, не зависящих друг от друга (дрожание пола от проехавшего мимо лаборатории транспорта, тепловое движение молекул, нестабильность параметров электронной схемы, выключающей электромагнит и т.д.). Из главной предельной теоремы, доказываемой в курсе теории вероятностей, следует, что по какому бы закону не были распределены отклонения, вызываемые каждой из причин, результат их совместного действия приведет к нормальному статистическому распределению результатов измерений. Такое нормальное распределение (распределение Гаусса) имеет вид:

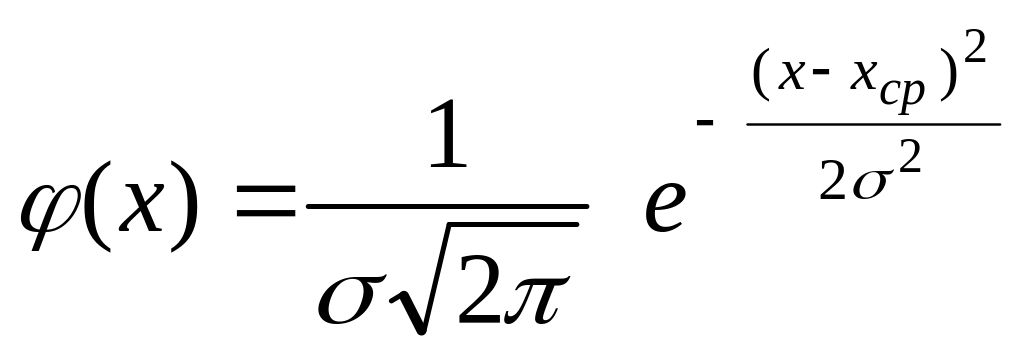. (1.1)

Если максимум кривой равен А, то величина есть расстояние от линии x_ср =100 см до кривой на высоте 0,6 А. Величина называется стандартной ошибкой (иначе среднеквадратичным отклонением) и характеризует точность метода измерений, то есть точность каждого измерения. Величина называется дисперсией распределения . Для конечного числа измерений n стандартная ошибка определяется как

, (1.2)

где x_i – i-е измерение, n – число измерений, x_ср – среднее ариф­метическое значение всех измерений:

. (1.3)

В физическом практикуме все измерения считаются имеющими нормальные распределения, хотя в общем случае это не всегда так.