2.5. Метод простой итерации (метод последовательных приближений)
Чтобы применить метод простой итерации для решения нелинейного уравнения F(x)=0, необходимо преобразовать его к следующему виду:
. (2)
Это преобразование
(приведение
уравнения к виду, удобному для итерации)
можно выполнить различными способами;
некоторые из них будут рассмотрены
ниже. Функция
называется итерационной
функцией.
Выберем каким-либо
образом приближенное значение корня
и подставим его в правую часть уравнения
(2). Получим значение
.
Подставим теперь
в правую часть уравнения (2), имеем
.
Продолжая этот процесс неограниченно,
получим последовательность приближений
к корню, вычисляемых по формуле
. (3)
Если существует
предел построенной последовательности
,
то, переходя к пределу в равенстве (3) и
предполагая функцию
непрерывной, получим равенство
(4)
Это значит, что
–
корень уравнения (2).
Рис. 9
Метод допускает простую геометрическую интерпретацию. Построим графики функций у = x и у = (x), (рис. 10,а и 10,б). Корнем уравнения у = (x) является абсцисса точки пересечения кривой
у = (x) с прямой у = x. Взяв в качестве начальной произвольную точку x0 [a, b], строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня . Из рисунков видно, что если '(x)<0 на отрезке [a, b], то последовательные приближения xn = (xn-1), колеблются около корня , если же производная '(x)>0, то последовательные приближения сходятся к корню монотонно.
a)
б)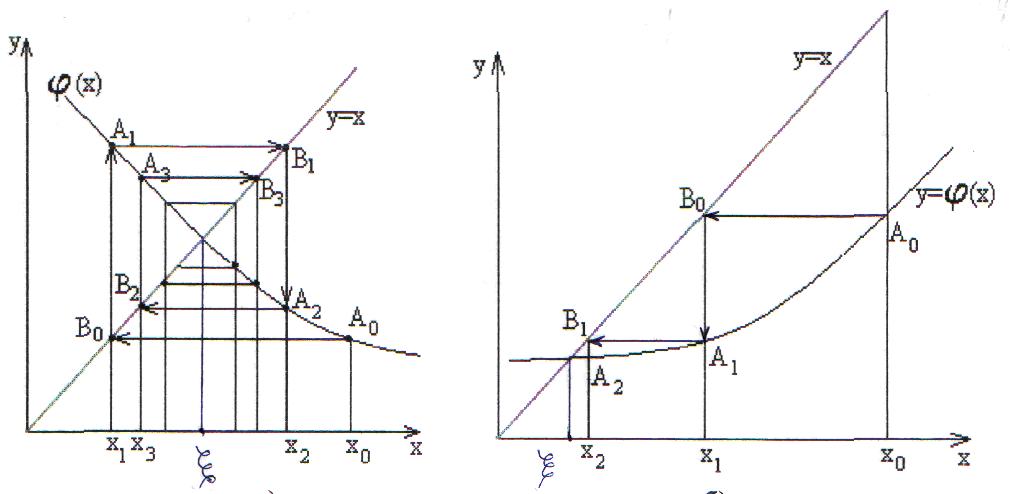
Рис. 10
При использовании метода простых итераций основным моментом является выбор функции у = (x), эквивалентной исходной.
На
рис. 11 рассмотрен пример, когда условие
окончания итерационного процесса
выполняется на первом шаге итерационного
процесса, т.е.
,
из этого следует, что х0
является приближенным значением искомого
корня. Однако из рис. 11 видно, что это
неверно, т.к. решением задачи является
.
Для метода итераций следует подбирать функцию (x) так, чтобы |'(x)| δ <1, в противном случае процесс итерации расходящийся. При этом следует помнить, что скорость сходимости последовательности {xn} к корню тем выше, чем меньше число δ.
Ключевой момент в применении метода простой итерации – эквивалентное преобразование уравнения F(x)=0 к виду (2). Конечно,
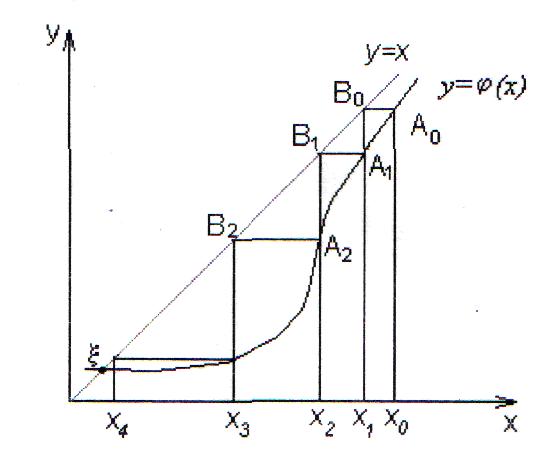
Рис. 11
такое преобразование
имеет смысл только тогда, когда оказывается
выполненным условие
при
.
Если
первая (обычно самая простая и
напрашивающаяся)
попытка представления уравнения в
требуемом виде оказалась
неудачной, отчаиваться не следует. В
ряде случаев можно использовать
специальные приемы. Рассмотрим некоторые
из них [2,5].
Способ
1.
Если
содержит в себе выражение некоторой
обратимой
на [с;
d]
функции
,
причем такой, что
на [c;
d],
то следует попытаться заменить уравнение
на равносильное
с использованием обратной для
функции
:
.
Этот способ основан на известном
соотношении между производными
взаимообратных функций
и
следствии из
него:
то
.
Пример.
Привести
уравнение
к виду, пригодному для решения методом
простой итерации на интервале [0,8; 2].
Прибавим к правой
и левой частям х
и получим:
.
Проверим условие сходимости:
условие сходимости не выполняется.
Другой вариант
уравнения:
.
Проверим условие сходимости:
условие сходимости не выполняется.
Так как ни одно из приведенных нами уравнений не удовлетворяет условию сходимости, то применим описанный способ:
;
условие
сходимости выполняется. Таким
образом, для уточнения нужного нам корня
методом простой итерации можно
использовать уравнение
.
Способ 2. В случае, когда способ 1 применить трудно или он не даст нужного результата, можно использовать следующий прием.
Пусть
дано уравнение с единственным корнем
в [a;
b].
Предположим,
что на отрезке [с;
d]
производная
функции F
непрерывна, не равна константе и принимает
значения
одного и того же знака. Будем считать,
что
,
т.к. в противном
случае можно рассматривать равносильное
уравнение:
.
Введем
обозначения:
.
Ясно,
что
.
Заменим равносильное
уравнение
уравнением эквивалентным ему
и
покажем, что для функции
на [c;
d]
имеет место условие сходимости.
Для
справедливы неравенства:
.
Разделим
их почленно на число М
и для разностей между единицей и
полученными
дробями получим неравенство:
,
откуда и вытекает, что
при всех .
Пример № 1.
Привести
уравнение
к виду, пригодному для решения методом
простой итерации на интервале [1,4; 1,7].
Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:
;
;
;
Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение
.
Пример № 2.
Привести
уравнение
к виду, пригодному для решения методом
простой итерации на интервале [1,7; 2,1].
Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:
Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение
.
Пример № 3.
Привести
уравнение
к виду, пригодному для решения методом
простой итерации на интервале [0,3;0,7].
Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:
;
Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение
.
Блок схема алгоритма метода простой итерации представлена на рис.12, где c – корень уравнения; n – число итераций; F(c) – значение функции в соответствующей точке.
Рис. 12