Лабораторная работа №2 методы отыскания решений нелинейных уравнений с одним неизвестным

Цель работы: решить нелинейное уравнение с заданной точностью .

Порядок выполнения работы

1. Познакомиться с описанием лабораторной работы.

2. Решить заданный вариант (см. п. 4):

а) отделение корня,

б) уточнение значения корня.

3. Составить отчет.

4. Ответить на контрольные вопросы.

5. Защитить лабораторную работу.

1. Постановка задачи

Задача нахождения корней нелинейного уравнения встречается в различных областях научных исследований и актуальна в наши дни. Она часто является элементарным шагом при решении научных и технических задач. Аналитические методы для нахождения корней нелинейных уравнений существуют лишь для отдельных уравнений, например, . Как правило, для нахождения корней используются приближенные методы. Нелинейные уравнения могут быть двух типов: алгебраические и трансцендентные. Уравнения вида называются алгебраическими, уравнения вида – трансцендентными, так как они содержат трансцендентные функции. К ним относят тригонометрические функции , экспоненциальную функцию , логарифмические функции .

В общем случае нелинейные уравнения с одним неизвестным имеют вид

. (1)

Корнем уравнения является всякое число действительное или мнимое, обращающее (1) в тождество.

Корни находятся в два этапа: первый – отделение корней, т.е. нахождение отрезка [a, b], содержащего один корень уравнения; второй – уточнение значения корней на найденных отрезках с заданной точностью .

Если функция непрерывна и принимает на концах отрезка

[a, b] разные знаки, т.е. и сохраняет на этом отрезке знак первой производной, то внутри этого отрезка находится один корень уравнения. Отделение корней можно осуществить различными способами.

1. Составляют таблицу значений функции на выбранном отрезке изменения аргумента. Для отделения корня необходимо, чтобы на концах выделенного отрезка функция имела разные знаки и была монотонна. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной. От заданной функции найдем и вычислим ее значения на концах отрезка [a, b], если , функция монотонна.

2. Строят график функции на отрезке изменения x; точка пересечения графика с осью даст нам корень уравнения. Для последующего уточнения корня возьмем окрестности корня и обозначим их [a, b].

3. Уравнение заменяют равносильным ему , строят два графика и 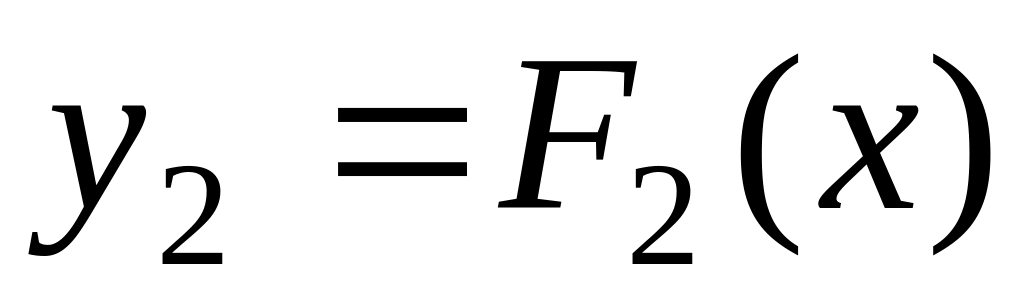. Абсцисса точки пересечения этих графиков, спроецированная на ось , даст нам отрезок [a, b], внутри которого находится корень уравнения .

2. Методы решения нелинейных уравнений

2.1. Метод деления пополам (метод бисекций)

Задача. Найти решение нелинейного уравнения с точностью .

Метод состоит в следующем: в результате отделения корня найден отрезок [a, b], в котором расположено искомое значение корня. В качестве начального приближения корня возьмем значение c_o=(b+a)/2. Далее исследуем значения на концах отрезков [a, c_o] и [c_o, b]. Тот из них, на концах которого примет значения разных знаков, содержит искомый корень. Поэтому его принимают в качестве нового отрезка (см. рис. 1, здесь корень находится на отрезке [c_o, b]). Затем полученный отрезок делим пополам и вновь производим проверку знаков. .

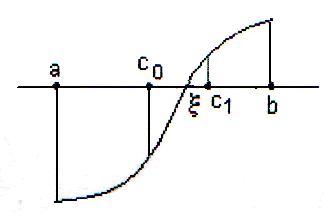
Рис. 1

Теперь корень находим на отрезке [c₀, c₁]. Затем находим и т.д. Итерационный процесс продолжается до тех пор, пока не станет меньше заданного числа : . Рабочая формула для нахождения корня имеет вид

.

Число итераций в этом методе зависит от предварительно задаваемой точности и длины отрезка [a, b] и не зависит от вида функции .

Метод медленный, всегда сходится, можно получить решение с заданной точностью, широко применяется на практике [5].

Блок-схема алгоритма метода половинного деления представлена на рис. 2, где [a, b] – отрезок, в котором находится корень уравнения;

с – корень уравнения; n – число итераций; - значение функции в соответствующей точке.