Задание

1. Задача об аудиторской проверке. Для проверки аудитор извлекает из информационной системы компании выборку накладных, заполненных в течение последнего месяца. Средняя сумма накладных за последние пять лет равна 120 долл. Аудитор должен оценить, изменилась ли сумма накладных.

Данные о суммах (в долларах) по 12 накладным:

108,98 152,22 111,45 110,59 127,46 107,26 93,32 91,97 111,56 75,71 128,58 135,11.

2. Произведены замеры объема лимонада в 50 двухлитровых бутылках. Данные приведены ниже:

2,109 2,086 2,066 2,075 2,065 2,057 2,052 2,044 2,036 2,038

2,031 2,029 2,025 2,029 2,023 2,020 2,015 2,014 2,013 2,014

2,012 2,012 2,012 2,010 2,005 2,003 1,999 1,996 1,997 1,992

1,994 1,986 1,984 1,981 1,973 1,975 1,971 1,969 1,966 1,967

1,963 1,957 1,951 1,951 1,947 1,941 1,941 1,938 1,908 1,894

Можно ли утверждать, что средний объем жидкости в бутылках отличается от 2 литров?

3. Компания, производящая батарейки для ручных фонариков, создала выборку из 13 батареек, произведенных за смену, и подвергла их испытанию на длительность работы. Ниже приведено количество часов, которое проработала каждая батарейка до момента отказа.

342 426 317 545 264 451 1049 631 512 266 492 562 298

Можно ли утверждать, что средняя продолжительность работы батареек больше 400 часов?

4. Решить задачу 3, заменив первое значение в выборке с 342 на 1342.

5. В штате Нью-Йорк сберегательным банкам разрешено осуществлять страхование жизни. Чтобы страхование было прибыльным для банка, необходимо ускорить оформление страховки. Банк создал выборку, в которой указано время, затраченное на оформление 27 страховок в течение одного месяца. Данные приведены ниже:

73 19 16 64 28 28 31 90 60 56 31 56 22 18

45 48 17 17 17 91 92 63 50 51 69 16 17

Предыдущие исследования показывают, что средний срок оформления заявки равен 45 дням. Можно ли утверждать, что средний срок оформления изменился?

Лабораторная работа №3 Двухвыборочные критерии

Проверка гипотезы на основе двух выборок из двух генеральных совокупностей основывается на критериях, которые называются двухвыборочными. Примерами таких задач могут служить такие: равны ли средние оценки студентов при двух разных методах обучения или равны ли средние недельные объемы продаж определенного товара, размещенного на специализированных стеллажах и на обычных полках.

В большинстве ситуаций дисперсии и стандартные отклонения двух генеральных совокупностей неизвестны. Единственная доступная информация – выборочные средние, выборочные дисперсии и стандартные отклонения. Если выборки являются случайными, независимыми и извлечены из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию, для проверки гипотезы о значимом различии между математическими ожиданиями двух генеральных совокупностей можно применять t-критерий, использующий суммарную дисперсию.

Нулевая гипотеза состоит в том, что математические ожидания двух независимых генеральных совокупностей не отличаются друг от друга:

H₀ : ₁ = ₂, или ₁ – ₂ = 0.

Альтернативная гипотеза состоит в том, что математические ожидания не совпадают:

H₁ : ₁  ₂, или ₁ – ₂  0.

t-критерий для оценки разности между двумя математическими ожиданиями с помощью суммарной дисперсии вычисляется по формуле:

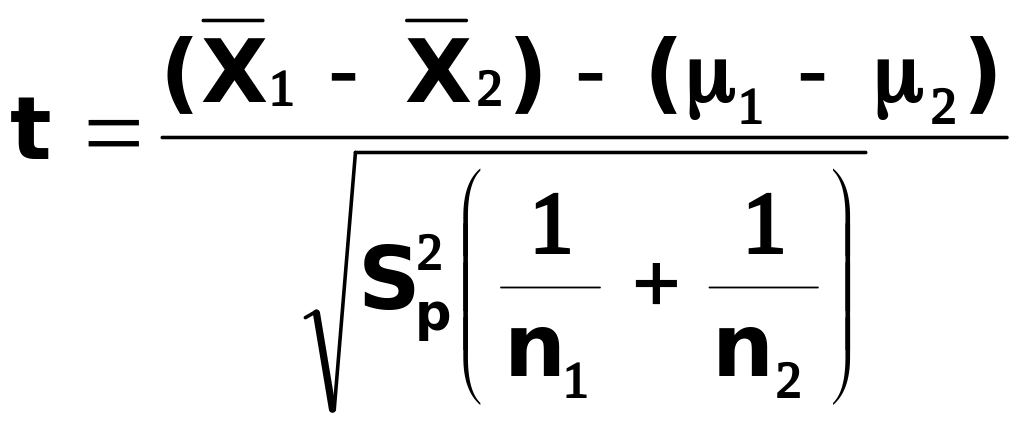(1)

Здесь – суммарная дисперсия; (2)

и – дисперсии первой и второй выборок;

n₁ и n₂ – объемы первой и второй выборок;

и – выборочные средние первой и второй выборок.

Статистика t , зависящая от суммарной дисперсии, имеет t-распределение Стьюдента с (n₁+n₂ – 2) степенями свободы. При заданном уровне значимости  двусторонний критерий отклоняет нулевую гипотезу, если t-статистика больше верхнего критического значения или меньше нижнего критического значения. Рассмотрим применение t-критерия на примере.

Задача 1. В большом университете был проведен эксперимент по преподаванию начальной биологии. Одна группа студентов обучалась по традиционному методу «лекции плюс лабораторные работы»; вторая группа – по методу «только лабораторные работы плюс демонстрации, без лекций». Студентов случайным образом распределили по указанным группам. В конце семестра все студенты сдавали экзамен; были получены случайные выборки оценок для каждой группы. Существует ли значимое различие в знаниях (оценках) студентов в зависимости от метода обучения?

Нулевая гипотеза состоит в том, что математические ожидания ( средние оценки) одинаковы, а альтернативная гипотеза – в том, что оценки отличаются.

Оценки студентов, обучавшихся по традиционной методике и с заменой лекций на демонстрации, приведены в таблице, размещенной на рабочем листе Excel.

	A	B
1	Традиц.	Демонстр.
2	55	56
3	57	60
4	60	62
5	63	67
6	72	70
7	73	71
8	79	82
9	85	88
10	92	95

Проверим, распределены ли статистические данные нормально, с помощью описательных статистик, для чего используем инструмент «Описательная статистика» надстройки Excel Анализ данных. Полученные результаты подтверждают тот факт, что данные, приведенные в выборках достаточно близки к нормальному распределению:

Традиц.		Демонстр.
Среднее	70,66667	Среднее	72,33333
Стандартная ошибка	4,317278	Стандартная ошибка	4,431579
Медиана	72	Медиана	70
Мода	#Н/Д	Мода	#Н/Д
Стандартное отклонение	12,95183	Стандартное отклонение	13,29474
Дисперсия выборки	167,75	Дисперсия выборки	176,75
Эксцесс	-1,09026	Эксцесс	-0,8032
Асимметричность	0,383564	Асимметричность	0,608065
Интервал	37	Интервал	39
Минимум	55	Минимум	56
Максимум	92	Максимум	95
Сумма	636	Сумма	651
Счет	9	Счет	9

Проверим с помощью t-критерия, значимо ли отличаются средние оценки этих двух групп. Для этого необходимо выполнить следующие действия:

• Сервис  Анализ данных  Двухвыборочный t-тест с одинаковыми дисперсиями .

• Заполнить поля диалогового окна Двухвыборочный t-тест с одинаковыми дисперсиями :

• Ввести в окне редактирования Интервал переменной 1 диапазон А1:А10 в соответствии с размещением данных на рабочем листе Excel.

• Ввести в окне редактирования Интервал переменной 2 диапазон В1:В10.

• В поле Гипотетическая средняя разность вводится значение разности между математическими ожиданиями генеральных совокупностей в соответствии с нулевой гипотезой H₀ : ₁ = ₂, или ₁ – ₂ = 0.

• Установить флажок Метки.

• Ввести в поле Альфа число 0,05.

• Установить переключатель Параметры вывода в положение Выходной интервал и ввести номер ячейки рабочего листа, с которой начать вывод результатов

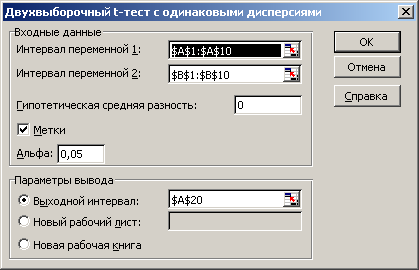
Рис.1. Диалоговое окно t-критерия

• Щелкнуть на кнопке ОК.

• Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные действия необходимо выполнить заново. Данные для этой процедуры должны быть разгруппированными, т.е. находиться в разных столбцах.

Анализ результатов применения t-критерия для проверки гипотезы о равенстве средних оценок студентов, обучающихся по двум разным методикам, (рис.2) дает основания утверждать следующее.

Поскольку t=-0, 2694, а t_кр = 2,1199, то значение t-статистики попадает в область принятия гипотезы. Наблюдаемый уровень значимости (p-значение) равен 0,7911 и больше уровня значимости, равного 0,05, а значит, нет оснований отвергать нулевую гипотезу. Таким образом, нет значимого различия в знаниях студентов, обучающихся по двум разным методикам.

Двухвыборочный t-тест с одинаковыми дисперсиями
	Традиц.	Демонстр.
Среднее	70,6666667	72,3333333
Дисперсия	167,75	176,75
Наблюдения	9	9
Объединенная дисперсия	172,25
Гипотетическая разность средних	0
df	16
t-статистика	-0,2693862
P(T<=t) одностороннее	0,39553782
t критическое одностороннее	1,74588367
P(T<=t) двухстороннее	0,79107564
t критическое двухстороннее	2,11990529

Рис.2. Результаты применения t-критерия

Следует отметить, что рассмотренный t-критерий с использованием суммарной дисперсии может применяться только для проверки гипотезы о разности между математическими ожиданиями двух генеральных совокупностей, дисперсии которых одинаковы. Если предположение о равенстве дисперсий ошибочно, суммарная дисперсия становится неприемлемой. Для решения этой проблемы Саттерсвейт предложил t-критерий, использующий раздельную дисперсию. Процедура использует две выборочные дисперсии. Она довольно сложна, поэтому для нее следует применять программу Microsoft Excel. Необходимо выполнить те же действия, что и для случая с одинаковыми дисперсиями, только вызвать инструмент Анализа данных Двухвыборочный t-тест с различными дисперсиями. Для рассмотренной задачи результат применения этого критерия не отличается от предыдущего. Однако в других ситуациях эти критерии могут привести к противоположным выводам. Поэтому выбирать критерий следует только после проверки предположения о равенстве дисперсий.

Все рассмотренные процедуры проверки гипотез применялись к двум независимым генеральным совокупностям. В том случае, когда элементы выборок являются парными результатами повторных измерений, выполненных в одном и том же множестве элементов, т.е. когда выборки являются зависимыми, интерес представляет разность между величинами, а не сами величины:

D_i = X_1i – X_2i , i = 1,2,…,n (3)

Цель исследования двух зависимых выборок – выявить различия между результатами двух измерений, уменьшив влияние изменчивости, присущей элементам выборки

Для оценки средней разности между средними значениями двух зависимых выборок величины D_i рассматриваются как наблюдения, принадлежащие одной и той же выборке. Поскольку в большинстве ситуаций стандартное отклонение генеральной совокупности неизвестно, то для исследований доступны лишь выборочные статистики. Если разности предполагаются случайными и независимыми величинами, имеющими нормальное распределение, для оценки разности между математическими ожиданиями зависимых генеральных совокупностей можно применить t-критерий, для чего вычислить t-статистику, имеющую t-распределение с n-1 степенями свободы. Несмотря на предположение о нормальном распределении генеральной совокупности, на практике при достаточно большом объеме выборки умеренной асимметрии выборочное распределение средней разности можно аппроксимировать t-распределением.

Нулевая и альтернативная гипотезы :

где ,

t-статистика вычисляется по формуле:

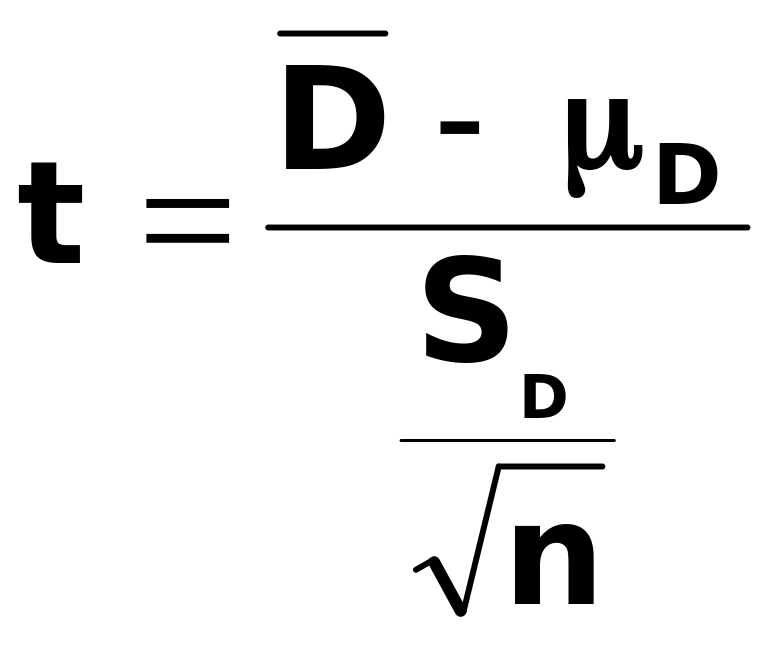, (4)

где - выборочное среднее, - выборочное стандартное отклонение.

При заданном уровне значимости  нулевая гипотеза отклоняется, если t-статистика больше верхнего или меньше нижнего критического значения t_кр.

Задача 2. Компания разрабатывает новое программное обеспечение для финансовых расчетов. Для оценки программного обеспечения разработчики провели эксперимент, в ходе которого один и тот же набор задач решали как с помощью лидера рынка стандартных программ, так и с помощью нового пакета. Можно ли утверждать, что новое программное обеспечение работает быстрее?

Поскольку измерения для каждой конкретной задачи проводились согласованно, для оценки эффективности пакета необходимо сравнить не средние значения двух независимых выборок, а среднюю разность между соответствующими элементами. Результаты эксперимента приведены в таблице, размещенной на листе Excel ( рис. 3).

Нулевая и альтернативная гипотезы формулируются следующим образом:

H₀ : _D  0 (в среднем стандартный пакет работает быстрее, чем новый),

H₁ : _D >0 (в среднем стандартный пакет работает медленнее, чем новый).

	A	B	C	D
1		Продолжительность	(сек)
2	Задача	Лидер	Новый	Разность (Di)
3	1	9,98	9,88	0,1
4	2	9,88	9,86	0,02
5	3	9,84	9,75	0,09
6	4	9,99	9,8	0,19
7	5	9,94	9,87	0,07
8	6	9,84	9,84	0
9	7	9,86	9,87	-0,01
10	8	10,12	9,86	0,26
11	9	9,9	9,83	0,07
12	10	9,91	9,86	0,05
13				0,084
14			SD	0,084354

Рис.3. Попарные измерения продолжительности работы

Установим уровень значимости  равным 0,05 и предположим, что разности распределены нормально. Применим t-критерий для парных выборок для проверки нулевой гипотезы. Применим процедуру Excel, для чего необходимо выполнить следующие действия.

• Сервис  Анализ данных  Парный двухвыборочный t – тест для средних .

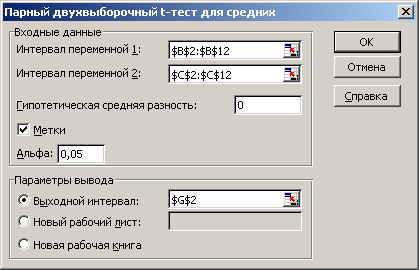
Рис.4. Заполнение полей диалогового окна.

• В диалоговом окне Парный двухвыборочный t – тест для средних заполнить поля:

• Ввести в окне редактирования Интервал переменной 1 диапазон В2 : В12 ;

• Ввести в окне редактирования Интервал переменной 2 диапазон С2 : С12 ;

• Ввести в окне редактирования Гипотетическая средняя разность число 0;

• Установить флажок Метки;

• Ввести в окне редактирования Альфа число 0,05;

• Установить переключатель Параметры вывода в положение Выходной интервал и ввести номер ячейки, определяющей верхний левый угол таблицы вывода результатов;

• ОК.

Результаты применения t-теста приведены на рис.5. Поскольку значение t = 3,149 лежит в критической области, нулевая гипотеза отклоняется. Поскольку p-значение равно 0, 0059 и меньше  = 0,05, нулевую гипотезу следует отклонить. Вычисленное p-значение означает, что если на самом деле оба пакета имеют одинаковую среднюю продолжительность работы при решении финансовых задач, то вероятность обнаружить превосходство нового пакета более чем на = 0,084 сек не превышает 0,0059. Поскольку эта величина очень мала, степень уверенности в нулевой гипотезе весьма невысока, и следует принять альтернативную гипотезу, т.е. признать, что стандартный пакет работает медленнее.

Парный двухвыборочный t-тест для средних
	Лидер	Новый
Среднее	9,926	9,842
Дисперсия	0,007448889	0,00159556
Наблюдения	10	10
Корреляция Пирсона	0,279753483
Гипотетическая разность средних	0
Df	9
t-статистика	3,149016086
P(T<=t) одностороннее	0,005878076
t критическое одностороннее	1,833112923
P(T<=t) двухстороннее	0,011756151
t критическое двухстороннее	2,262157158

Рис.5. Результаты применения t-критерия для парных выборок

Доверительный интервал, содержащий разность между математическими ожиданиями генеральных совокупностей, равен:

(5)

Таким образом, при доверительном уровне 95% средняя разность между продолжительностями работы двух пакетов колеблется в пределах

0,084  2,26220,0844/ , т.е. 0,0236  _D  0,1444.

Поскольку 0 не принадлежит этому интервалу, следует сделать вывод, что эффективность нового пакета выше, что подтверждает вывод, полученный с помощью t-критерия.