Міністерство освіти та науки україни
Придніпровська державна академія будівництва та архітектури
Кафедра «Прикладна математика»
Методичні вказівки
до виконання лабораторних робіт
з дисципліни
Інформаційні системи в менеджменті
Дніпропетровськ-2013
Інформаційні системи в менеджменті. Методичні вказівки. Для студентів всіх форм навчання академії. / Л.В.Цибрій. – Дніпропетровськ : ВНЗ «ПДАБА», 2013. – 69с.
Укладач : Цибрій Л.В.
Відповідальний за випуск Єршова Н.М., д.т.н., проф.,
Зав. каф. прикладної матем.
ПДАБА
Содержание
Лабораторная работа №1
Проверка гипотезы о нормальном распределении………………………………..4
Лабораторная работа №2
Проверка гипотезы о математическом ожидании………………………………..10
Лабораторная работа №3
Двухвыборочные критерии………………………………………………………..16
Лабораторная работа №4
Проверка гипотезы об однородности дисперсий………………………………...27
Лабораторная работа №5
Однофакторный дисперсионный анализ………………………………………….36
Лабораторная работа №6
Ранговый критерий…………………………………………………………………46
Лабораторная работа №7
Двуфакторный дисперсионный анализ…………………………………………...56
Лабораторная работа №8
Проверка гипотезы об однородности выборок…………………………………...68
Содержание контрольного задания……………………………………………….69
Лабораторная работа №1 Проверка гипотезы о нормальном распределении
Нормальное распределение является непрерывным, причем нормально распределенная случайная величина принимает произвольные значения, лежащие на всей числовой оси. Кривая распределения симметрична, так что все характеристики среднего значения случайной величины – математическое ожидание, мода и медиана – совпадают друг с другом. На графике приведена кривая распределения случайной величины с матожиданием, равным 1.
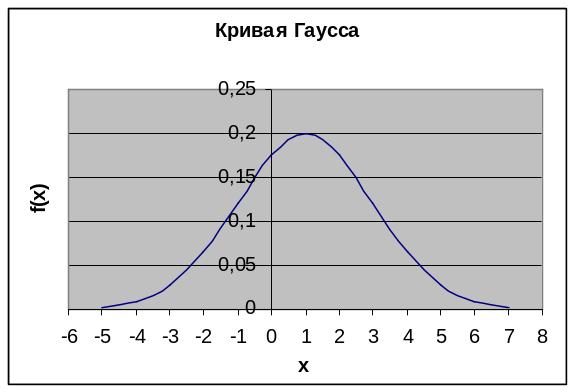
На практике характеристики статистических данных могут немного отличаться от теоретических либо потому, что случайная величина является лишь приближенно нормально распределенной, либо потому, что ее реальные свойства отличаются от предполагаемых. В таких случаях кривая распределения оказывается не совсем симметричной и колоколообразной. Кроме того, диапазон изменения данных не может быть бесконечным. Для того, чтобы проверить, является ли данная случайная величина нормально распределенной, т.е. проверить гипотезу о нормальном распределении, следует выполнить следующие действия.
Построить график нормального распределения, гистограмму и оценить их внешний вид.
Вычислить описательные статистики и сравнить их с теоретическими свойствами нормального распределения. Вычислить моду и медиану и определить, совпадают ли они с выборочным средним. Вычислить стандартное отклонение и определить диапазон изменения случайной величины. Проверить, сильно ли он отличается от величины, равной шести стандартным отклонениям.
Оценить распределение данных: лежат ли две трети наблюдений в окрестности среднего значения радиуса не более одного стандартного отклонения.
С построением гистограммы и вычислением описательных статистик с помощью инструментов надстройки Excel Анализ данных мы познакомились в курсе «Математическое моделирование управленческих задач». График нормального распределения – это двумерный график, на вертикальной оси которого отложены наблюдаемые данные, а на горизонтальной оси – соответствующие квантили стандартизованного нормального распределения. Если точки, соответствующие наблюдаемым данным, лежат на графике близко к прямой, проведенной из левого нижнего угла в правый верхний угол, значит, данные распределены приближенно нормально. В противном случае распределение отличается от нормального.
Для того чтобы построить график нормального распределения, необходимо выполнить следующие действия.
Упорядочить набор данных по возрастанию.
Вычислить квантили стандартизованного нормального распределения.
Построить график в координатах «квантили – наблюдаемые значения».
Оценить вероятность того, что анализируемая случайная величина является хотя бы приближенно распределенной нормально, по отклонениям точек от прямой линии, проведенной из нижнего левого угла в верхний правый угол графика.
Квантили вычисляются только в соответствии с упорядоченными по возрастанию исходными данными. Первый квантиль стандартизованного нормального распределения представляет собой стандартизованную нормально распределенную величину Z, которой соответствует площадь фигуры, лежащей под кривой плотности вероятностей, равная 1/(n+1). Второй квантиль – площади 2/(n+1); i-ый квантиль – площади i/(n+1); n-ый квантиль – площади n/(n+1). Математическое ожидание стандартизованного нормального распределения равно 0, а стандартное отклонение – 1. Поскольку это распределение симметрично, его медиана также равна 0. Следовательно, квантили стандартизованного нормального распределения, не превышающие медиану, являются отрицательными, а превышающие медиану – положительными. Квантили этого распределения вычисляются с помощью обратного преобразования нормально распределенных данных.
Построим график стандартизованного нормального распределения для данных, представляющих оценки девяти студентов (n=9), обучающихся по традиционному методу. Размещение информации на листе Excel может быть таким:
|
A |
B |
C |
D |
1 |
i |
Площадь |
Z |
Оценки |
2 |
1 |
0,1 |
-1,28155 |
55 |
3 |
2 |
0,2 |
-0,84162 |
57 |
4 |
3 |
0,3 |
-0,5244 |
60 |
5 |
4 |
0,4 |
-0,25335 |
63 |
6 |
5 |
0,5 |
-1,4E-16 |
72 |
7 |
6 |
0,6 |
0,253347 |
73 |
8 |
7 |
0,7 |
0,524401 |
79 |
9 |
8 |
0,8 |
0,841621 |
85 |
10 |
9 |
0,9 |
1,281552 |
92 |
В ячейки B2 и C2 вводятся формулы, которые копируются до 10–ой строки:
|
B |
C |
2 |
=A2/10 |
=НОРМСТОБР(B2) |
График стандартизованного нормального распределения строится как точечная диаграмма по данным столбцов C и D.
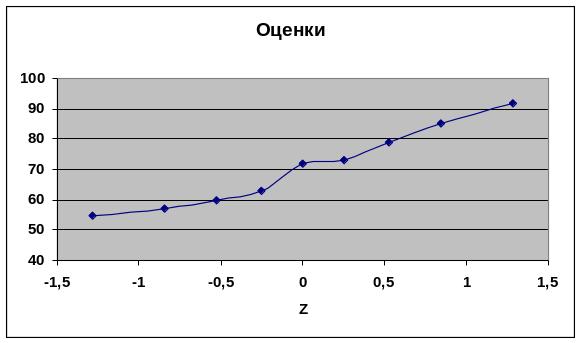
Рис. 1. График стандартизованного нормального распределения
Если на графике вертикальная ось проходит через значение Z = 0, ее необходимо перевести в крайнее левое положение, как показано на рис.1.
Для этого нужно:
– установить курсор на ось X и щелкнуть правой кнопкой ;
– во всплывающем меню выбрать команду Формат оси;
– в диалоговом окне Формат оси щелкнуть на корешке вкладки Шкала и ввести крайнее левое значение Z в окне Ось Y (значений) пересекает в значении ;
– щелкнуть OK.
На рис.2 показано заполнение полей для задачи об оценках.
Приведенный график стандартизованного нормального распределения позволяет сделать вывод, что данные не противоречат гипотезе о нормальном распределении, поскольку точки достаточно близко расположены к прямой, проходящей через крайние точки графика.
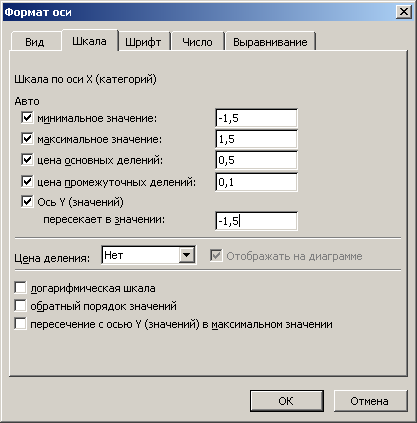
Рис.2. Заполнение полей диалогового окна Формат оси.
Этот же вывод подтверждают значения описательных статистик и гистограмма. Среднее выборочное (среднее) и медиана достаточно близки.
Оценки |
|
|
|
Среднее |
70,66667 |
Стандартная ошибка |
4,317278 |
Медиана |
72 |
Мода |
#Н/Д |
Стандартное отклонение |
12,95183 |
Дисперсия выборки |
167,75 |
Эксцесс |
-1,09026 |
Асимметричность |
0,383564 |
Интервал |
37 |
Минимум |
55 |
Максимум |
92 |
Сумма |
636 |
Счет |
9 |
Наибольший(1) |
92 |
Наименьший(1) |
55 |
Рис.3. Описательные статистики
Значение выборочного среднего зависит от всех элементов выборки, поэтому наличие экстремальных значений значительно влияет на результат. В таких случаях следует указывать и медиану. Медиана как срединное значение упорядоченного массива чисел делит его пополам, т.е. половина элементов массива, если он не содержит повторяющихся чисел, окажется меньше медианы, а половина – больше медианы. У нормально распределенной случай-ной величины среднее и медиана совпадают. Чем ближе их значения, тем больше распределение приближается к нормальному, как и в приведенном примере. У нормального распределения асимметричность и эксцесс равны 0. Чем ближе к 0 эти статистики, тем ближе распределение к нормальному.
Гистограмма, построенная процедурой Анализ данных – Гистограмма
может содержать неточности: пробелы между столбцами и нежелательные метки. Чтобы удалить пробелы между столбцами диаграммы, следует щелкнуть правой кнопкой мыши на одном из столбцов гистограммы и в появившемся контекстном меню выбрать команду Формат рядов данных
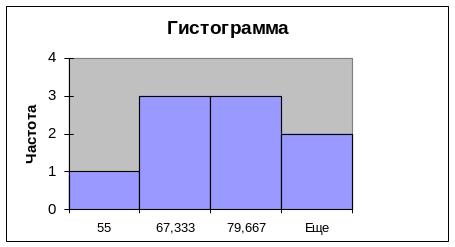
Рис.4. Гистограмма
В диалоговом окне щелкнуть на корешке вкладки Параметры и установить значение Ширина зазора, равным 0. Щелкнуть OK.
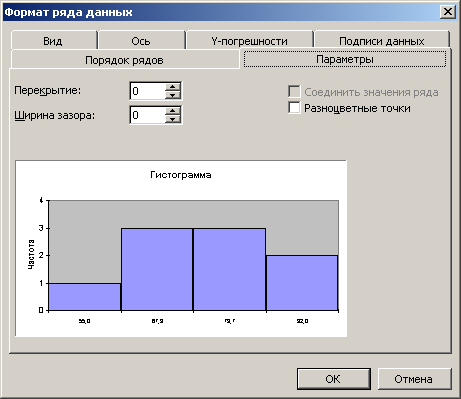
Рис.5. Корректировка гистограммы
Гистограмма близка к нормальной кривой и подтверждает незначительную положительную асимметрию, следующую из описательной статистики и из графика стандартизованного нормального распределения, в котором точки расположены в основном несколько ниже прямой, соединяющей крайние точки графика.
Задание. В таблице приведены массивы оценок, полученные студентами при сдаче четырех тестов по финансовому делу. Проверить гипотезу о нормальном распределении оценок по каждому тесту.
I |
II |
III |
IV |
64 |
73 |
55 |
62 |
60 |
66 |
53 |
53 |
48 |
47 |
47 |
38 |
82 |
83 |
83 |
92 |
52 |
54 |
48 |
41 |
78 |
82 |
76 |
89 |
72 |
78 |
66 |
80 |
66 |
75 |
57 |
68 |
55 |
58 |
50 |
44 |
58 |
76 |
59 |
71 |
75 |
80 |
72 |
86 |
57 |
61 |
51 |
47 |
62 |
71 |
54 |
59 |
70 |
77 |
64 |
77 |
58 |
64 |
52 |
50 |
69 |
77 |
62 |
74 |
65 |
74 |
56 |
65 |
61 |
68 |
53 |
56 |
73 |
79 |
69 |
83 |