Переходные процессы в цепях первого и второго порядка Общие сведения
Используемые для анализа линейных электрических цепей установившиеся процессы, при которых напряжения и токи постоянные величины либо гармонические функции времени, практически не реализуемы, так как все физические процессы имеют начало и конец. Следовательно, любое непериодическое изменение воздействия, изменение конфигурации цепи или параметров входящих в нее элементов приводит к тому, что режим цепи становится неустановившимся. Любое скачкообразное изменение в цепи, приводящее к неустановившемуся режиму, принято называть коммутацией. Нестационарные процессы, возникающие в цепи при переходе от одного установившегося режима к другому, называются переходными.
Возникновение переходных процессов в цепи обусловлено наличием в ней реактивных элементов (индуктивностей и емкостей), в которых накапливается энергия магнитного и электрического полей. При коммутации изменяется энергетический режим работы цепи, причем эти изменения не могут осуществляться мгновенно, поскольку скорость изменения энергии P=dW/dt мощность, отдаваемая или потребляемая соответствующими элементами цепи, не может быть бесконечно большой.
Это положение носит название принципа непрерывности во времени суммарного потокосцепления и суммарного электрического заряда цепи, из которого следует непрерывность токов в индуктивностях и напряжений на емкостях. Вывод о непрерывности токов в индуктивностях и напряжений на емкостях формулируется в виде законов коммутации.
Первый
закон коммутации:
в начальный момент времени после
коммутации ток в индуктивности имеет
такое же значение, как и непосредственно
перед коммутацией, и с этого значения
плавно изменяется:
.
Второй
закон коммутации:
в начальный момент времени после
коммутации напряжение на емкости имеет
такое же значение, как и непосредственно
перед коммутацией, и с этого значения
плавно изменяется:
.
Следует отметить, что в цепях с идеализированными элементами скачкообразно могут изменяться: а) напряжения на R и L; б) токи в R и С.
Значения тока в индуктивности и напряжения на емкости в момент коммутации (t=0) называются независимыми начальными условиями.
В основе всех методов расчета переходных процессов в линейных цепях лежит составление интегро-дифференциальных уравнений для мгновенных значений токов и напряжений. Эти уравнения составляются на основе уравнений Кирхгофа, метода контурных токов, метода узловых потенциалов и после несложных преобразований приводятся к линейному неоднородному дифференциальному уравнению с постоянными коэффициентами
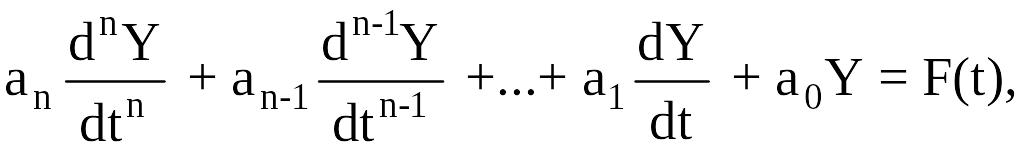
где
y(t)
искомая функция
(ток или напряжение);
постоянные коэффициенты, зависящие от
параметров цепи; F(t)
известная функция, зависящая от внешнего
воздействия.
Существуют
различные способы решения дифференциальных
уравнений с постоянными коэффициентами.
В частности, можно использовать
классический метод, согласно которому
решение уравнения находится в виде
суммы двух функций:
,
где
частное решение
определяет принужденный
(вынужденный)
режим работы цепи, задаваемый внешними
источниками (правой частью уравнения
F(t)
= de/dt
),
общее решение
однородного дифференциального уравнения
(при F(t)=0)
характеризует электрические процессы,
обусловленные изменением начального
электрического состояния цепи в
отсутствии внешних источников свободные
(собственные)
составляющие.
Таким
образом,
.
Для определения принужденной составляющей переходного процесса в цепи можно воспользоваться любыми известными методами расчета линейных цепей в установившемся режиме после коммутации.
Характеристическое уравнение, соответствующее данному дифференциальному уравнению цепи при F(t) = 0:
Если все корни характеристического уравнения простые, свободная составляющая переходного процесса имеет вид
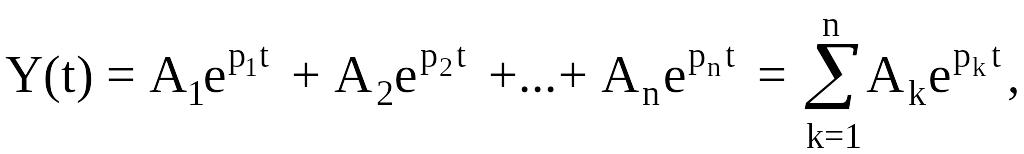
где
постоянные интегрирования, определяемые
по начальным условиям (значениям
искомых токов или напряжений и их n-1
первых производных в начальный момент
времени после коммутации).
Так как начальный запас энергии в реактивных элементах цепи всегда ограничен, то при наличии потерь свободные составляющие с течением времени затухают, и при t стремящемся к бесконечности, в цепи будет наблюдаться только принужденный режим.
На основании законов коммутации
откуда
т. е. начальные значения свободных составляющих определяются изменениями в момент коммутации соответствующих принужденных функций.