Лабораторная работа №3

Исследование переходных процессов в цепях второго порядка

Цель работы: экспериментальное исследование переходных процессов RLC-цепи при подключении к генератору прямоугольных видео- и радиоимпульсов.

Краткие сведения

Если RLC-цепь (рис. 3.1) , не имеющая начального запаса энергии электрического и магнитного полей, подключается к источнику внешнего напряжения в момент времени t = 0, то для t > 0 справедливо уравнение

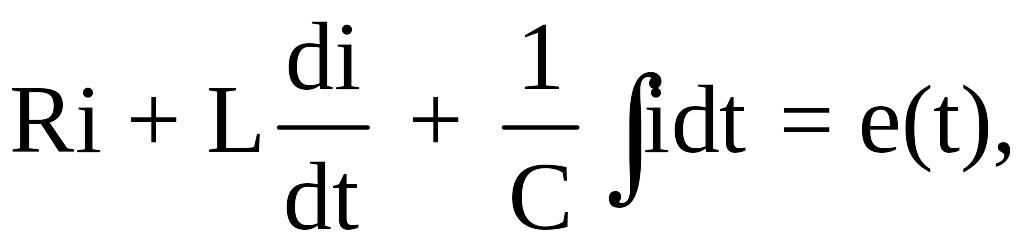
имеющее решение для тока

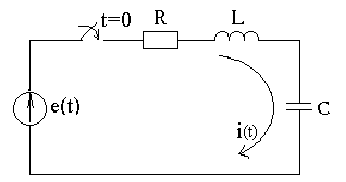
Рис. 3.1

Свободная составляющая

где и корни характеристического уравнения

,

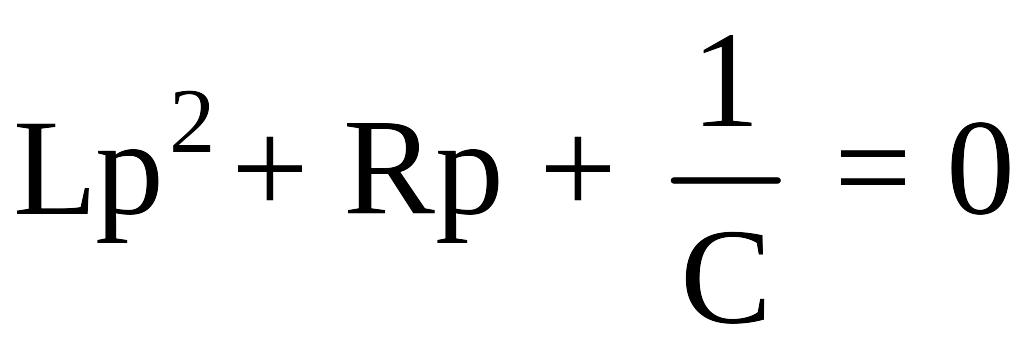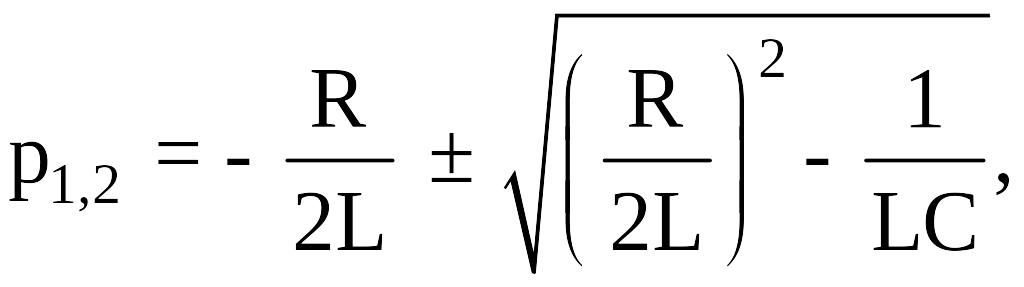
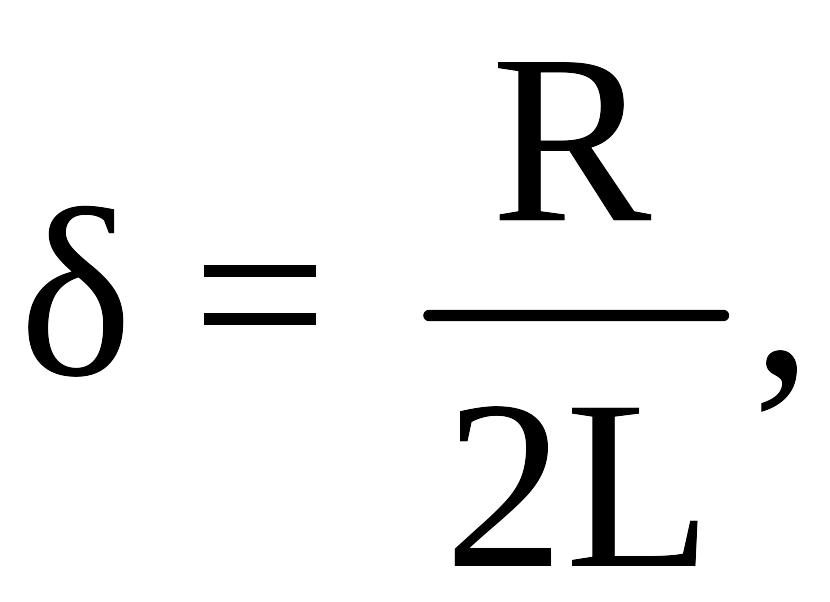
Обозначив 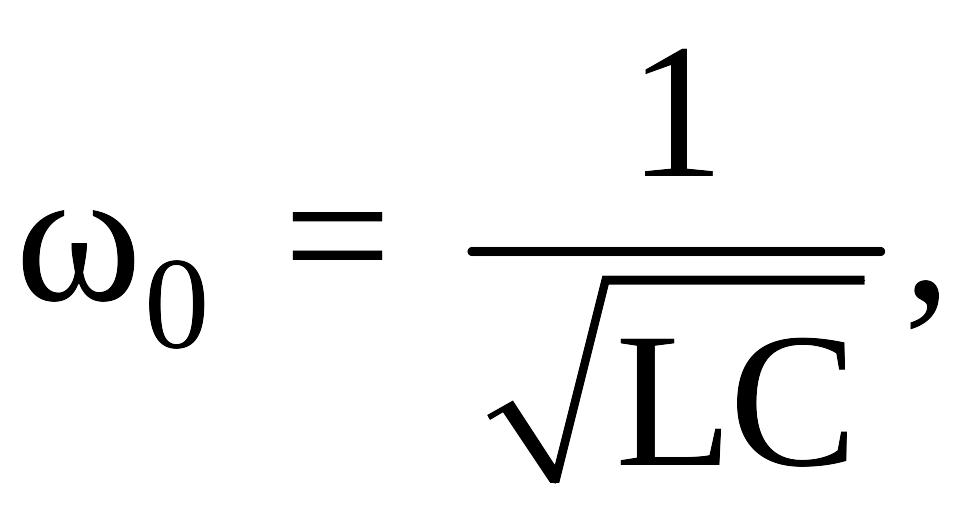получим

и  постоянные интегрирования, определяемые начальными условиями в цепи;  принужденная составляющая тока, определяемая видом ЭДС e(t) и величинами R, L, C.

При подключении источника постоянного напряжения = 0, так как постоянный ток через конденсатор не течет:

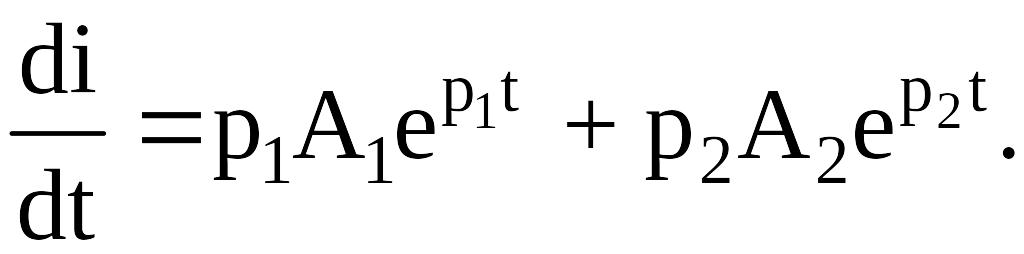
Для t = 0

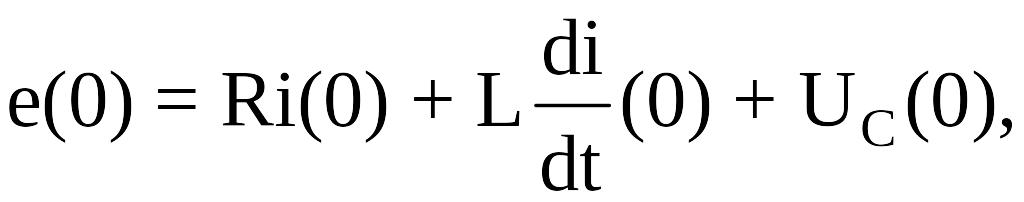
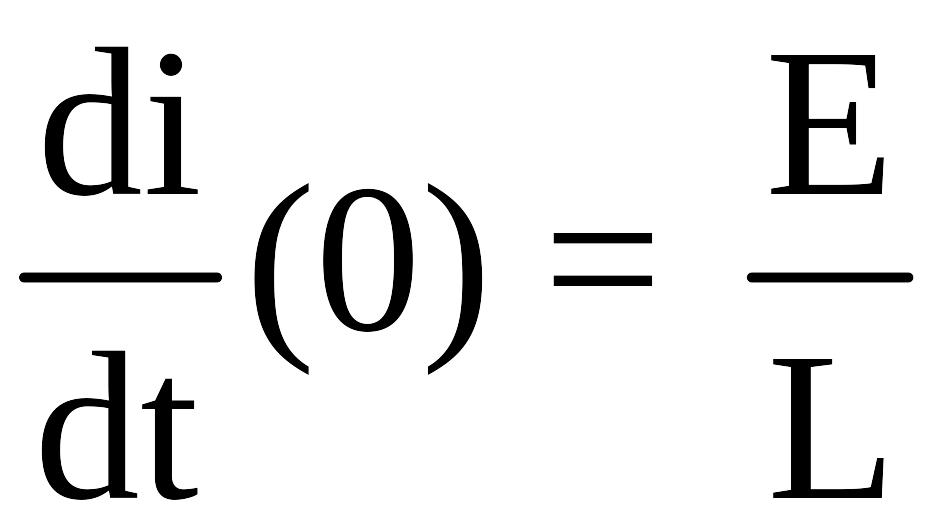
(т. к. ).

Таким образом,

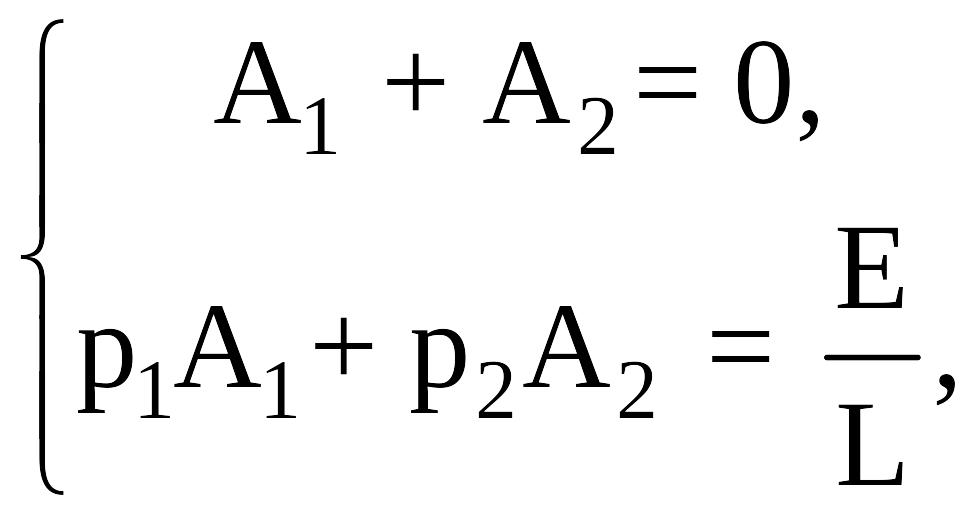
откуда

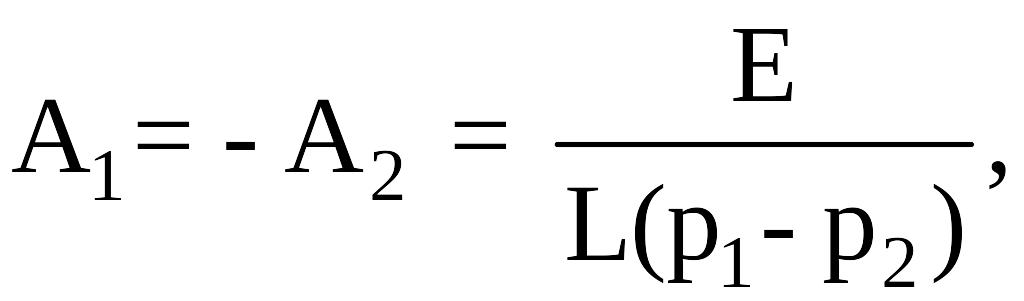
следовательно,

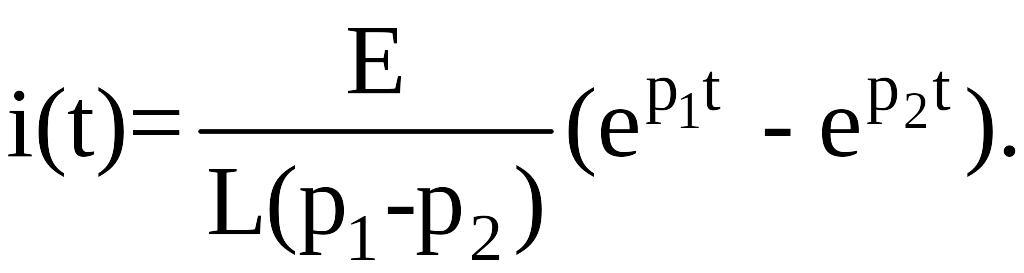
В зависимости от соотношения и (  резонансная частота) возможны три случая:

а) ,

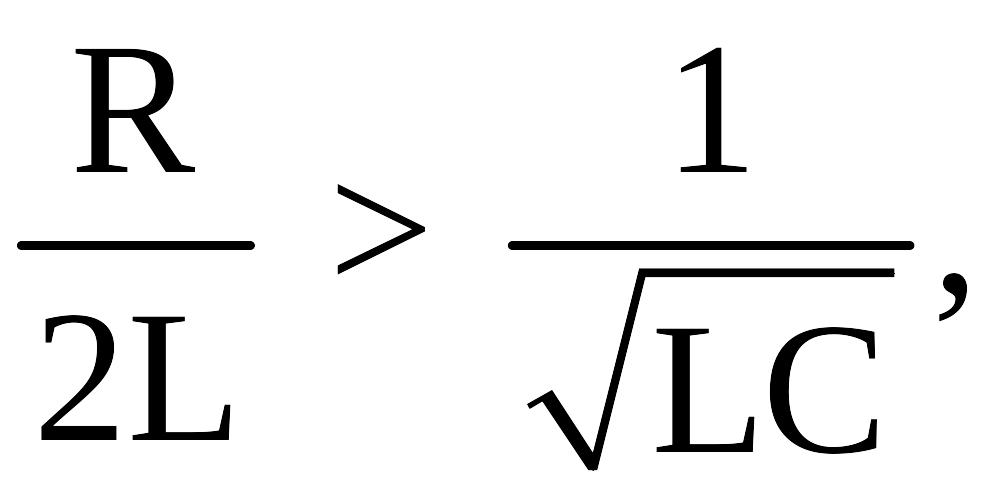
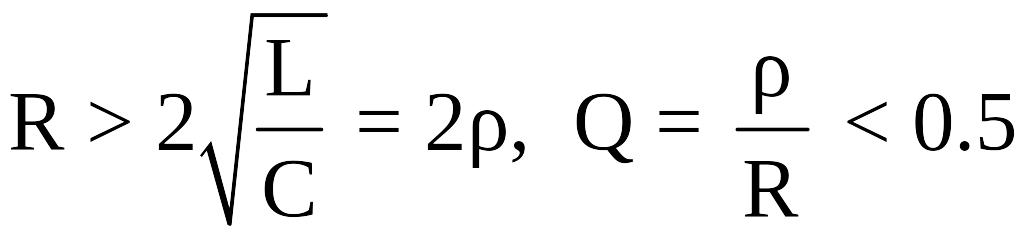
(апериодический процесс).

В плоскости комплексного переменного корни характеристического уравнения лежат на вещественной оси (рис. 3.2). Ток в цепи представляет собой сумму двух экспонент (рис. 3.3) .

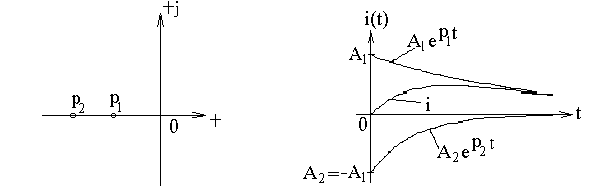
Рис. 3.2 Рис. 3.3

Напряжения на элементах:

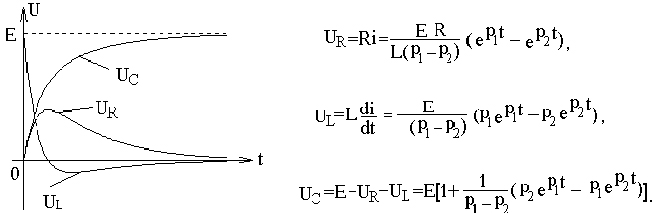
Рис. 3.4

Графики зависимостей от времени приведены на рис. 3.4.

б) , R Q = 0,5 (критический режим).

= -  в этом случае выражение для тока приводит к неопределенности вида 0/0, раскрывая которую по правилу Лопиталя, получим

,

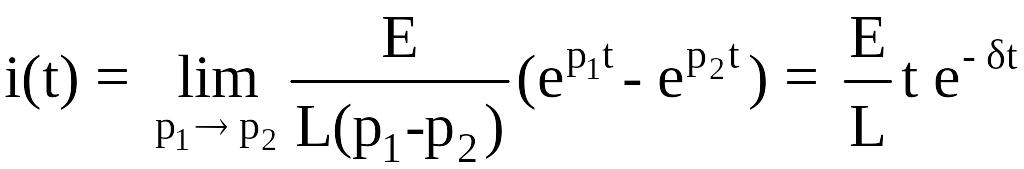при ненулевых начальных условиях

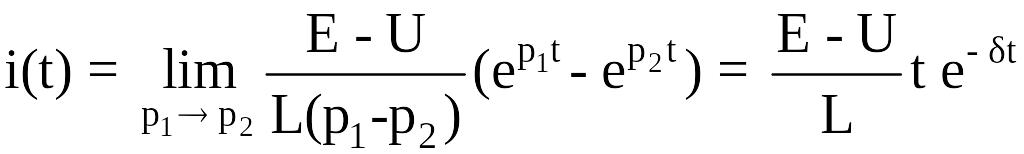
(действительно, дифференцированием числителя и знаменателя по , получаем

.

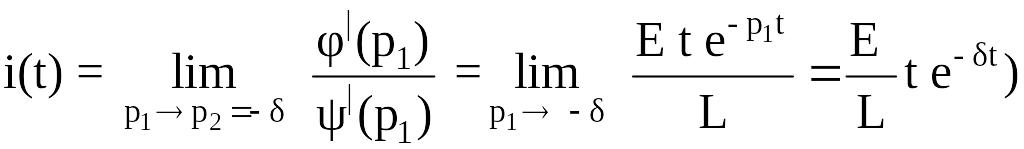Форма кривых зависимостей тока и напряжений на R, L, C от времени аналогична апериодическому режиму, условие Q = 0,5 является предельным условием существования в цепи апериодических процессов.

в) , R < 2, Q > 0,5, = - j (колебательный процесс).

Корни характеристического уравнения комплексно-сопряженные (рис. 3.5).

 угловая частота свободных (собственных) колебаний.

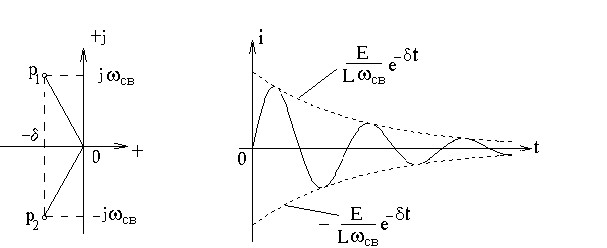
Рис. 3.5 Рис. 3.6

При

.

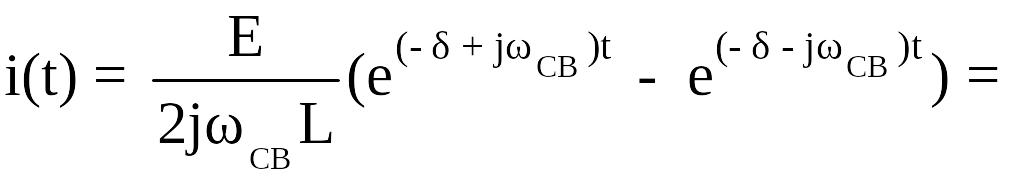
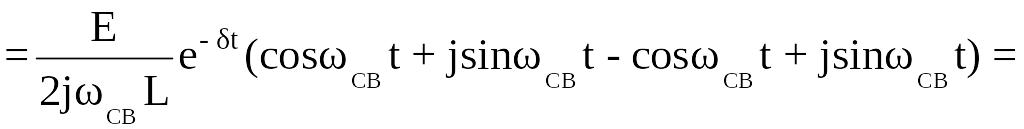
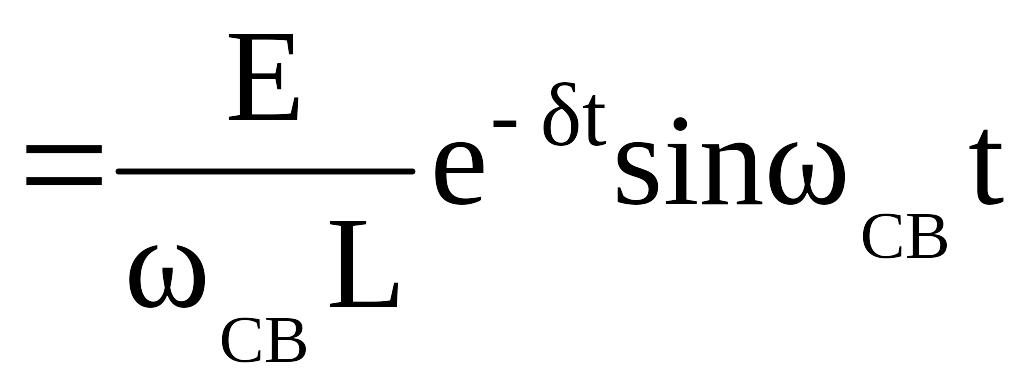Таким образом, ток в цепи представляет собой затухающую гармоническую функцию, амплитуда которой экспоненциально уменьшается во времени (рис. 3.6).

Напряжение на элементах цепи:

,

,

,

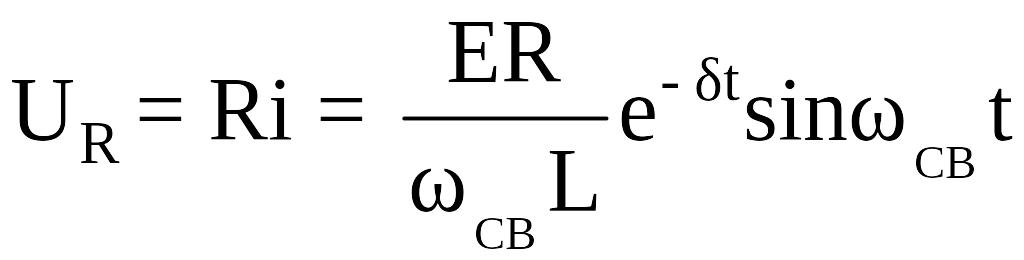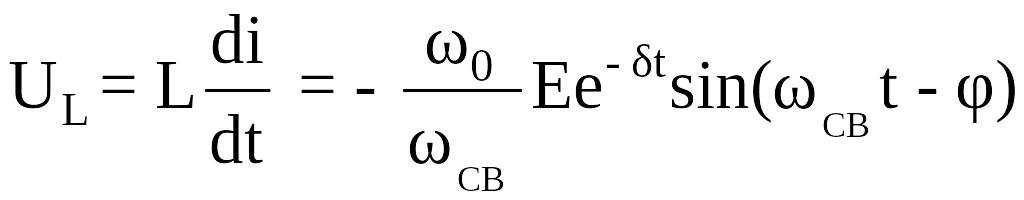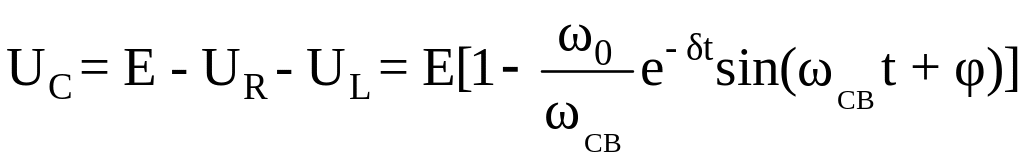где .

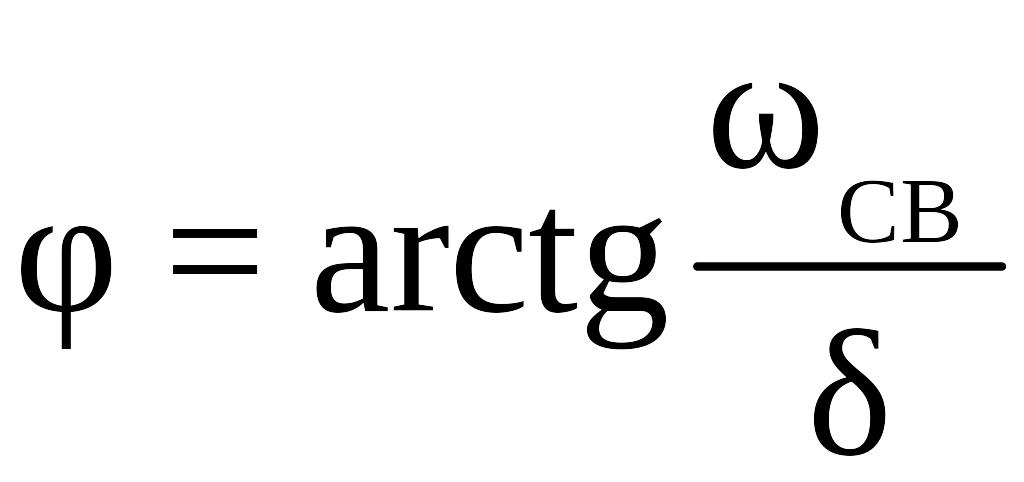Графики зависимостей от времени приведены на рис. 3.7.

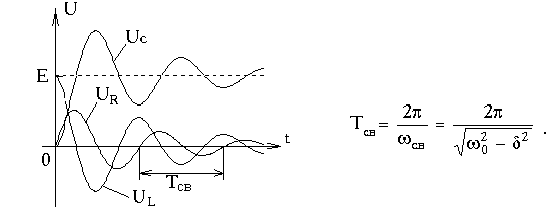
Рис. 3.7

Очевидно, что чем меньше , тем медленнее затухают колебания в цепи.

Скорость затухания колебаний оценивают величиной  декрементом затухания, где  период свободных колебаний, а также логарифмическим декрементом затухания .