Теоретический материал

Для вычисления значения определённого интеграла на практике широко ис-

пользуют квадратурные формулы – приближённые равенства вида

Здесь , некоторые точки из отрезка [a,b] – узлы квадратурной формулы;

Ai –числовые коэффициенты, называемые весами квадратурной формулы. Сумма , принимаемая за приближённое значение интеграла, называется квадратурной суммой.

Если для любого многочлена P(x) степени не выше m квадратурная формула даёт точное значение интеграла, то говорят, что квадратурная формула точна для многочленов степени m.

Существует несколько простейших квадратурных формул. Разобьем отрезок [a,b] на элементарные отрезки некоторыми точками . Интеграл при этом:

Пусть шаг при этом будет постоянным, тогда:

Приблизим на каждом элементарном отрезке площадь криволинейной трапеции площадью прямоугольника, тогда просуммировав по всем элементарным отрезкам, для площади криволинейной трапеции имеем квадратурную формулу прямоугольников:

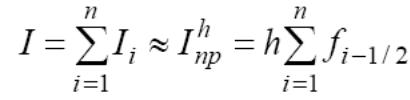
Так же используют формулы правых и левых прямоугольников:

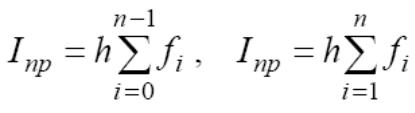
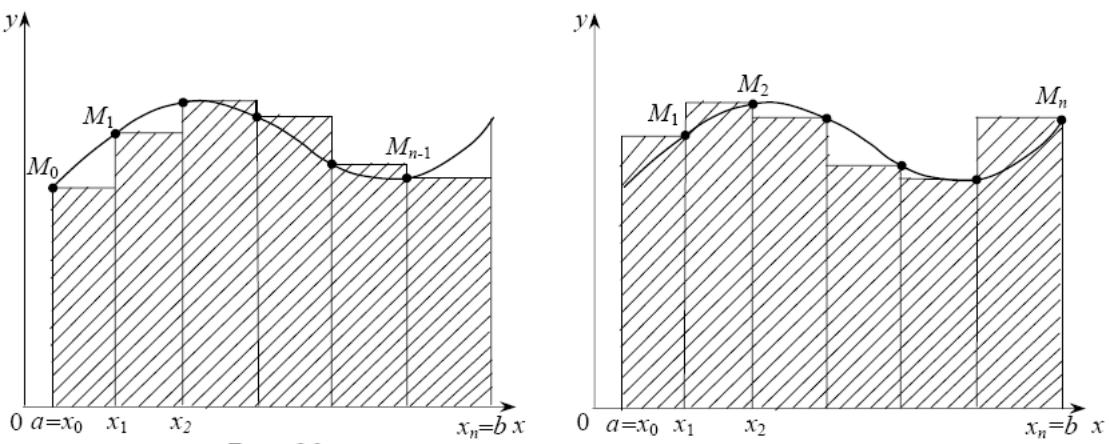
Приблизим на каждом элементарном отрезке площадь криволинейной трапеции площадью трапеции, тогда получим:

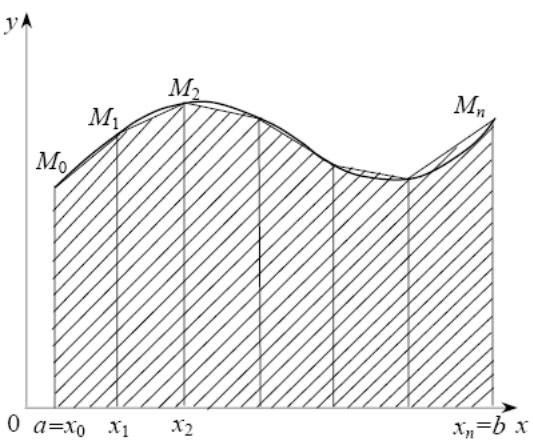
Вывод формулы Симпсона развивает описанный подход дальше. Но теперь для аппроксимации функции используется не кусочно-линейное, а кусочно-квадратичное интерполирование. Будем считать n чётным и сгруппируем отрезки парами, для каждого двойного отрезка построим интерполяционный полином Лагранжа второго порядка. Тогда квадратурная формула Симпсона или парабол примет вид:

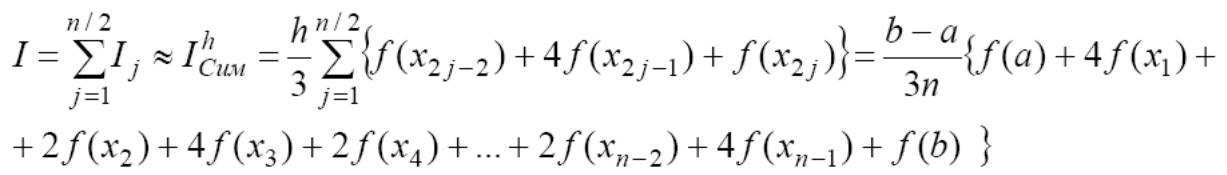
Предположим, что подынтегральная функция f достаточно гладкая и

Пусть функция f дважды непрерывно дифференцируема на (a,b). Тогда для составных квадратурных формул прямоугольников и трапеций справедливы следующие оценки погрешности, называемые также априорными оценками погрешности:

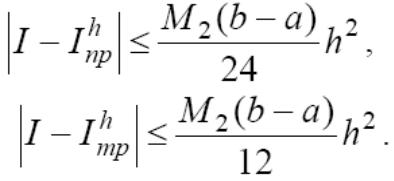
Пусть функция f на (a,b) имеет непрерывную производную четвёртого порядка. Тогда для формулы Симпсона справедлива оценка погрешности:

Интеграл представляют в виде суммы интегралов по элементарным отрезкам.

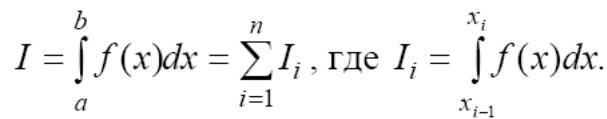
На каждом отрезке функцию f аппроксимируют легко интегрируемой функцией g(x). В результате получается составная формула:

Для интеграла составная квадратурная формула интерполяционного типа имеет вид:

Рассмотренные ранее простейшие квадратурные формулы являются частными случаями этой формулы, для случая равностоящих t, которые в этом случае относятся к классу формул Ньютона-Котеса.

Частый случай формулу Ньютона-Котеса при m=3 называется формулой 3/8:

И при m=4 формула Милана:

Квадратурная формула ,построенная интегрированием интерполяционного многочлена степени n с фиксированными узлами для всех многочленов степени n. Задача построения квадратурной формулы, точной для многочленов наиболее высокой степени, чем n, при заданном количестве (n +1) узлов за счёт выбора узлов приводит к квадратурной формуле Гаусса.

Квадратурная формула Гаусса для двух узлов имеет вид:

Квадратурная формула Гаусса при произвольном n является сложной задачей, но используя полиномы Лежандра эту задачу можно эффективно решить. Полиномы Лежандра обладают рядом свойств:

1. Узлы t0,t.1,...,tn−1 [−1,1]квадратурной формулы Гаусса с n узлами определяются как корни полинома Лежандра степени n;

2. Веса Ai из формулы (7.11) находятся из интегральных формул:

Квадратурная формула Гаусса для трех узлов имеет вид:

Квадратурная формула Гаусса для четырех узлов имеет вид:

где

Применение формул для априорной оценки погрешности в большинстве случаев не возможно, и не эффективно. Для оценки погрешности в таких случаях используют формулы для апостериорной оценки погрешности, в частности правило двойного пересчета.

Пусть I приближенное значение интеграла вычисленное по некой квадратурной формуле с постоянным или переменным шагом h, предположим:

Уменьшая шаг в два раза, мы уменьшаем погрешность в раз.

Правило двойного пересчета:

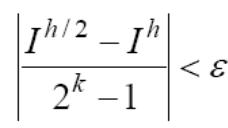
Для формулы прямоугольников и трапеций, правило двойного пересчета принимает вид:

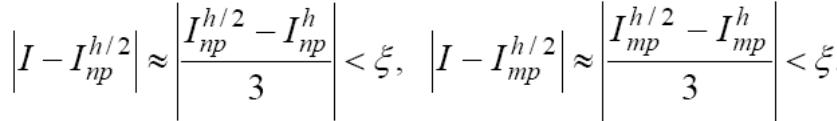
Для формулы Симпсона:

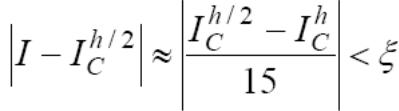
Для формулы Милана:

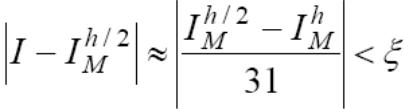
Результаты

Название формул	Приближенное значение интеграла	Число узлов
Априорная оценка
Центральных прямоугольников	32.7946388	9989161
Трапеций	32.7946325	1997832
Симпсона	32.7946325	1794826
3/8	32.7946309	2350
Милана	32.7946325	2350
Гаусс	30.5813955	2
	32.4579505	3
	32.7405068	4
Правило двойного пересчёта
Центральных прямоугольников	32.7946627	2097152
Трапеций	32.7946476	2048
Симпсона	32.7946685	64
3/8	32.7948709	16
Милана	32.7947351	8
Адаптивный метод
Центральных прямоугольников	32.7946681	9530211
Трапеций	32.7946346	8576
Симпсона	32.7946347	140
3/8	32.794641	36
Милана	32.7946325	36
Гаусс	32.4721563	2
	32.7537744	3
	32.7863914	4

Вывод: Применение адаптивного метода к формулам Гаусса приводят к увеличению точности решения, при этом, чем меньше количество узлов, тем сильнее увеличивается точность (у формул Гаусса с 2 и 3 узлами точность возросла очень сильно). Адаптивный метод улучшил точность формулы центральных прямоугольников, у остальных же только ухудшил. С увеличением узлов в формуле гаусса точность значительно увеличивается, особенно это заметно без применения адаптивного метода. Применение правила двойного пересчёта значительно увеличивает скорость достижения заданной точности.