Результаты вычислительного эксперимента

Р ешаем данное уравнение аналитически

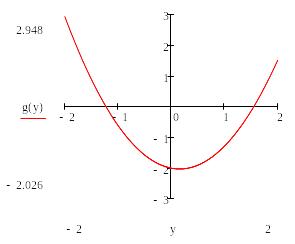
Рис.6

Используя встроенную функцию пакета MathCAD root(), находим корни уравнения:

При помощи составленных программ полученные корни равны:

Метод бисекции:

Метод Ньютона:

Метод секущих:

Метод Стефенсона:

Метод ложного положения:

В получившихся матрицах первый элемент – решение, второй элемент – количество итераций.

	Точное значение	Метод бисекции	Метод Ньютона	Метод секущих	Метод Стеффенсена	Ложного положения
x1	-1,22333	-1,22333	-1,22333	-1,22333	-1,22333	-1,22333
x2	1,55034	1,55034	1,55034	1,55034	1,55034	1,55034
n		20	5	8	7	3
∆		0	0	0	0	0,00001

где n – количество итераций, ∆ - погрешность решения.

Вывод

По количеству итераций методы: Метод ложного положения оказался самым эффективным. Метод бисекции в данном примере получился наименее эффективным по сравнению с остальными.

Для решения этой задачи были применены те же программы, которые были применены в 1 части данной лабораторной работы.

Численное решение систем линейных уравнений прямыми методами Постановка задачи 2.1

Заданы матрицы A u B системы уравнений порядка n в матричной форме Ax=B. Необходимо найти решение заданной системы уравнений. Для решения задачи использовать метод Гаусса. Исследовать зависимость погрешности для решения системы от погрешности задания правой части системы.

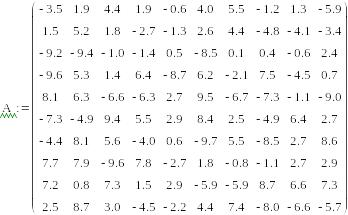
Теоретический материал

Метод Гаусса относится к прямым методам, позволяющим получить решение

системы после выполнения конечного числа операций. Метод Гаусса состоит

из двух основных этапов, называемых прямым ходом и обратным ходом. На

первом этапе система приводится к треугольному виду. Затем на втором этапе

осуществляется последовательное отыскание неизвестных.

Прямой ход состоит из n–1 шага исключения, после n-1 шага редуцируем систему к треугольному виду с верхней треугольной матрицей:

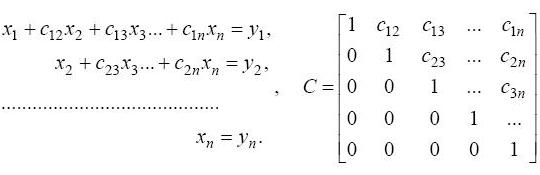
Обратный ход состоит в последовательном определении неизвестных из системы в обратном порядке.

Описанная выше процедура решения системы может оказаться неустойчивой

по отношению к случайным ошибкам. Чтобы избежать этого, естественно потребовать выполнения условия . Обеспечим выполнение неравенства для всех элементов треугольной матрицы С. Такой способ коррекции называется выбором ведущего элемента по строке. Матрицы, обладающие свойством , называются матрицами с диагональным преобладанием.