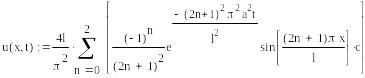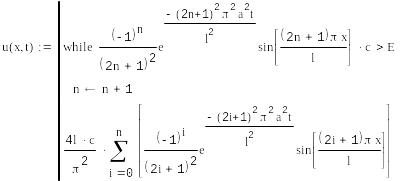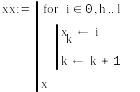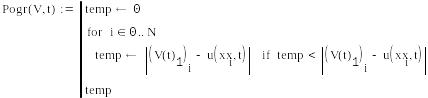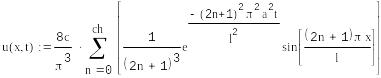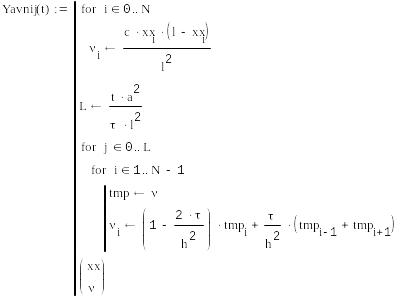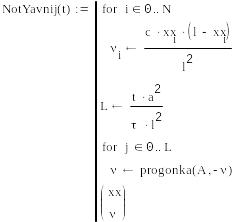Численное решение краевой задачи для одномерного и неоднородного уравнения теплопроводности.

Постановка задачи 9.1

Найти численное решение уравнения , удовлетворяющего условиям. При заданных значениях c,a.l. и T. Найти численное решение задачи на временно интервале [0;T], используя явную схему, неявную схему и схему Кранка - Николсона при весе

При условиях:

(46)

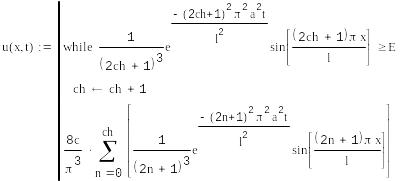
Дана функция, являющаяся аналитическим решением данного уравнения:

Теоретический материал

Процесс распространения тепла в одномерном стержне 0 < x < l описывается уравнением теплопроводности

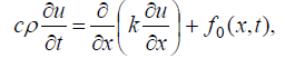(47)

где u = u(x,t) – температура в точке x в момент времени t, с – теплоёмкость единицы массы, ρ – плотность, сρ – теплоёмкость единицы длины, k – коэффициент теплопроводности, f0 – плотность тепловых источников. В общем случае k, с, ρ , f0 могут зависеть не только от x и t, но и от температуры u(x,t) . Если коэффициенты k, с, ρ постоянны, то (47) можно записать в виде

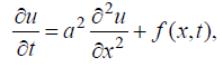
где a2 = k /(cρ ) – коэффициент температуропроводности. В дальнейшем без ограничения общности положим, что a =1, l =1. В самом деле вводя переменные x1 = x / l, 2 / 2 ,

t1 = a t l 2 2

f1 = l f / a , получим

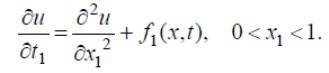
Будем рассматривать первую краевую задачу в области П={0 ≤ x ≤1;0 ≤ t ≤ T}.

Требуется найти непрерывное в области П решение u = u(x,t) задачи

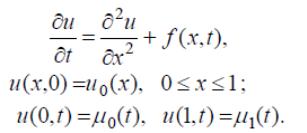(48)

(49)

(50)

Условие (48) характеризует начальное распределение температуры в стержне. Краевые условия (49), (50) характеризуют распределение температуры на концах стержня.

В области П введём сетку

с шагом h по x и с шагом τ по t. Заменяя вторую производную в (9.2) по x разностным выражением

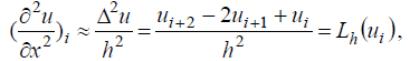
а первую производную по t разностным отношением

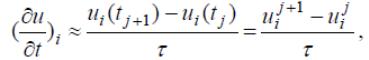
получим явную схему на 4-точечном шаблоне:

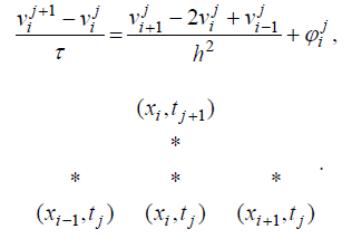(51)

Здесь , либо , и т. д. Дополнительные условия для определения сеточной функции v:

(52)

(53)

Значения на (j+1)-м временном слое находятся по явной формуле

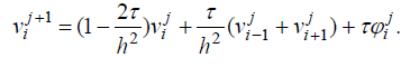
Если в разностной схеме Lh (ui ) все значения ui брать на (j+1)-м временном слое, то получаем полностью неявную схему с опережением на 4-х точечном шаблоне:

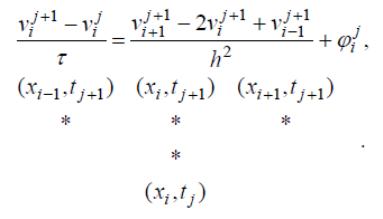(54)

Для определения j+1 vi из (54) получаем краевую задачу

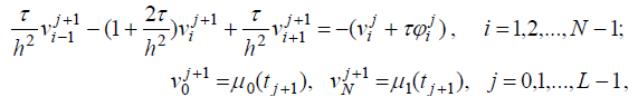
которая решается методом прогонки.

Если правую часть взять в виде линейной комбинации vi на (j+1)-м слое и j- м слое, то получим разностную схему с весами:

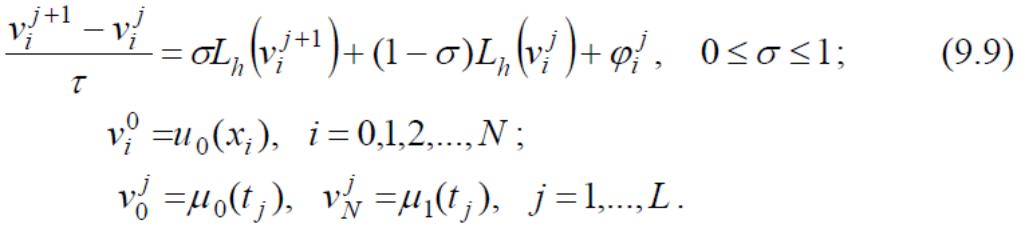(55)

Схема (55) определена на 6-точечном шаблоне:

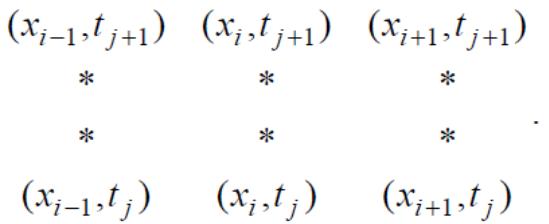
В случае σ =1 получается чисто неявная схема, а при σ = 0 – явная схема.

При весе σ =1/ 2 значения сеточной функции на новом слое определяются из краевой задачи:

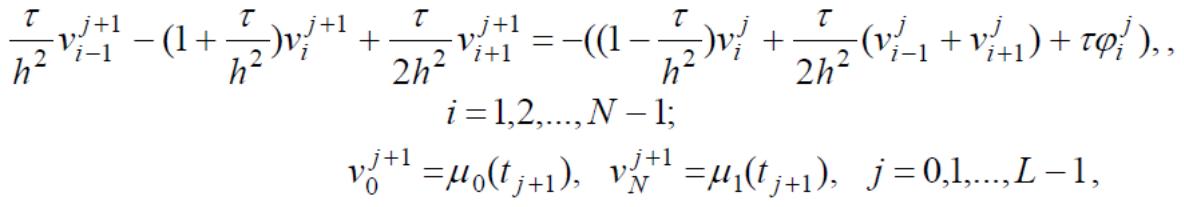
которая решается методом прогонки.

Результат вычислительного эксперимента

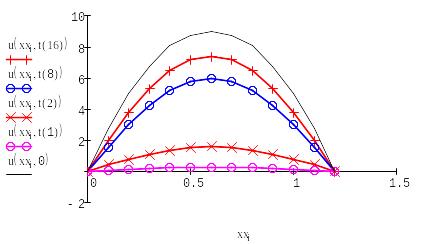
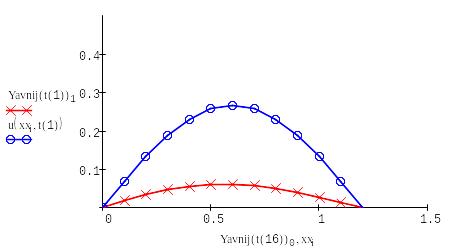
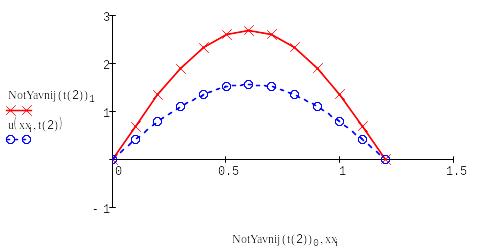
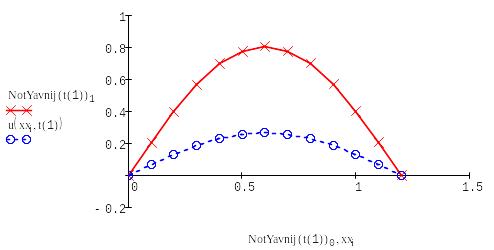
Построим график данной функции для каждого временного слоя, включая начальный:

Решение по явной схеме на различных слоях:

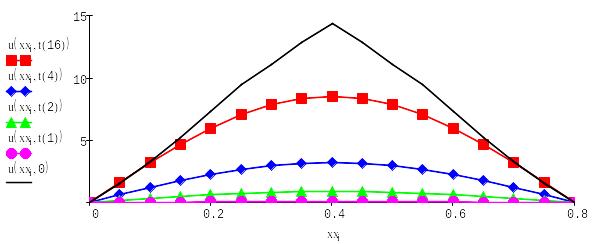
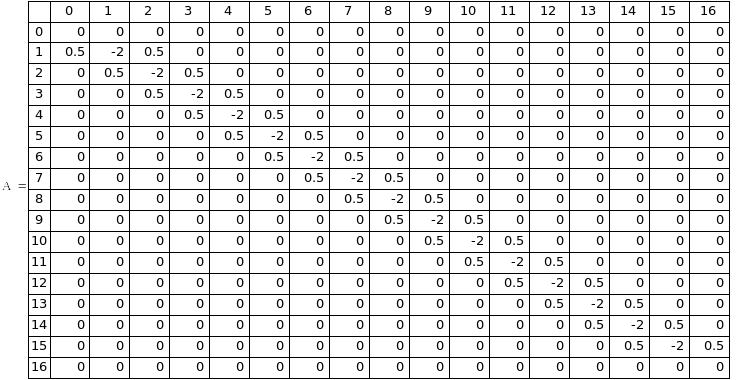
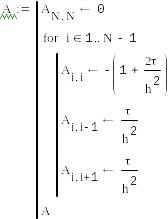
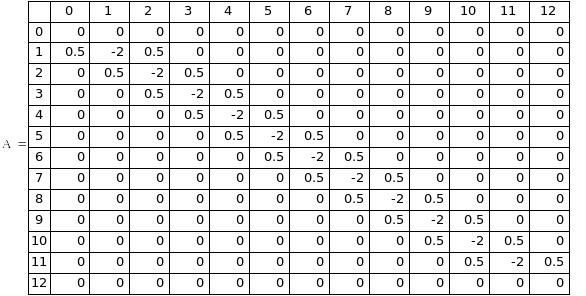
С помощью метода прогонки зададим трёхдиагональную матрицу А

Решение с помощью неявной схемы на различных слоях:

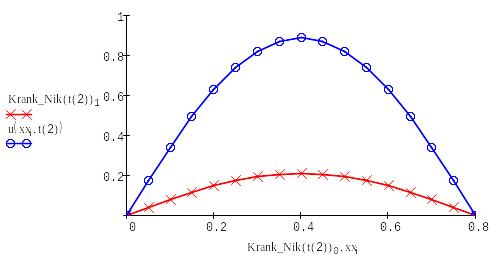
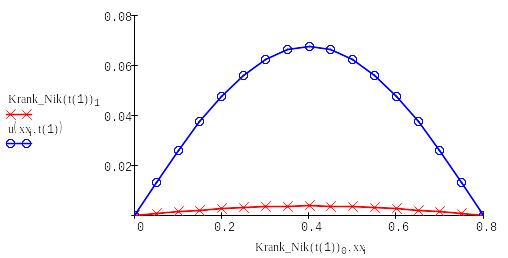
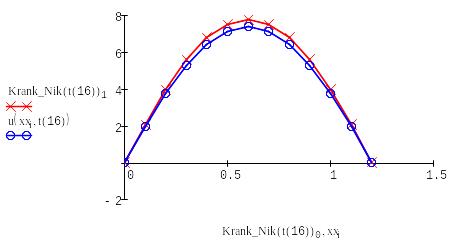
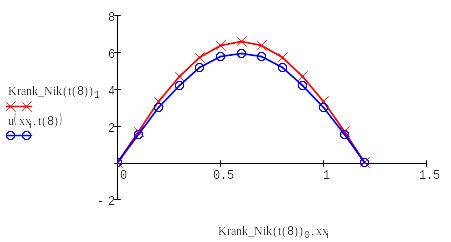
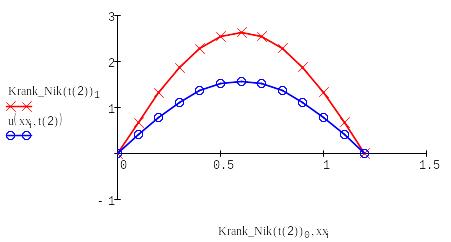
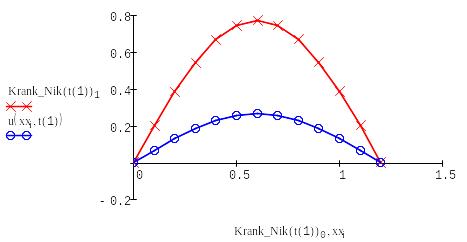
Находим решение с помощью формулы Кранка-Николсона:

Находим погрешности:

Выводим в одном графике все полученные решения:

Вывод

Проведя лабораторную работу, мы выяснили, что самый точный алгоритм - основанный на неявной схеме, а самый неточный - алгоритм на основе явной схемы.

Тексты программ

Постановка задачи 9.2

Дан тонкий однородный стержень длины l, изолированный от внешнего пространства, начальная температура . Концы стержня поддерживаются при температуре, равной нулю. Определить температуру стержня в заданный момент времени t. В таблице заданы значения c,a,l,T. Найти численное решение задачи на временном интервале [0;T], используя явную схему, неявную схему и схему Кранка-Николсона.

Дана функция, являющаяся аналитическим решением данного уравнения:

Результаты вычислительного эксперимента

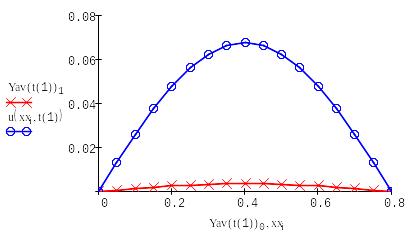
Построим график данной функции для каждого временного слоя, включая начальный:

Решение по явной схеме для различных слоев:

С помощью метода прогонки зададим трёхдиагональную матрицу А

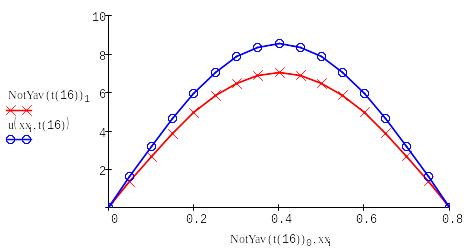
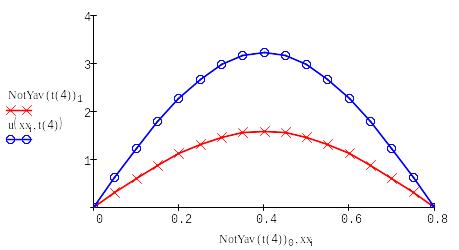
Решение с помощью неявной схемы для различных слоев:

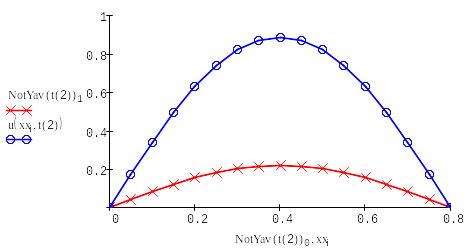
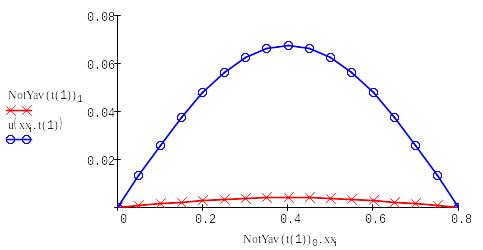
Находим решение с помощью формулы Кранка-Николсона :

Находим погрешности:

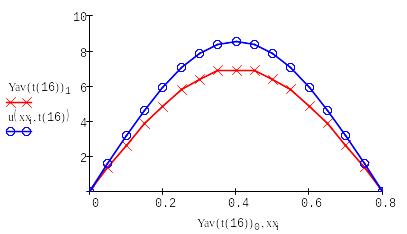
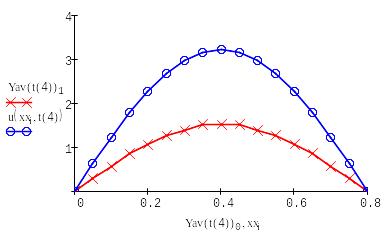
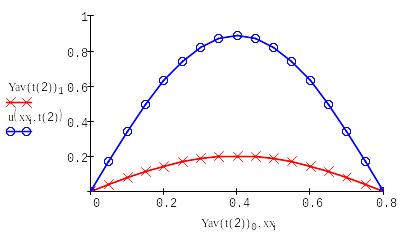
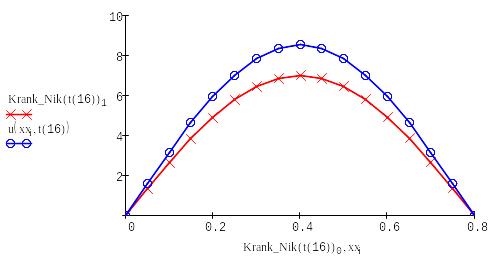
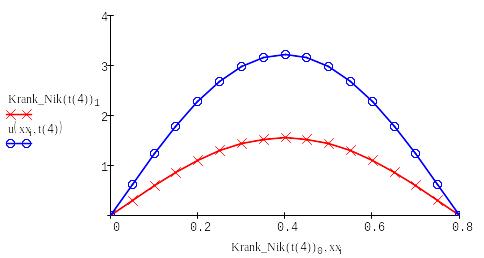
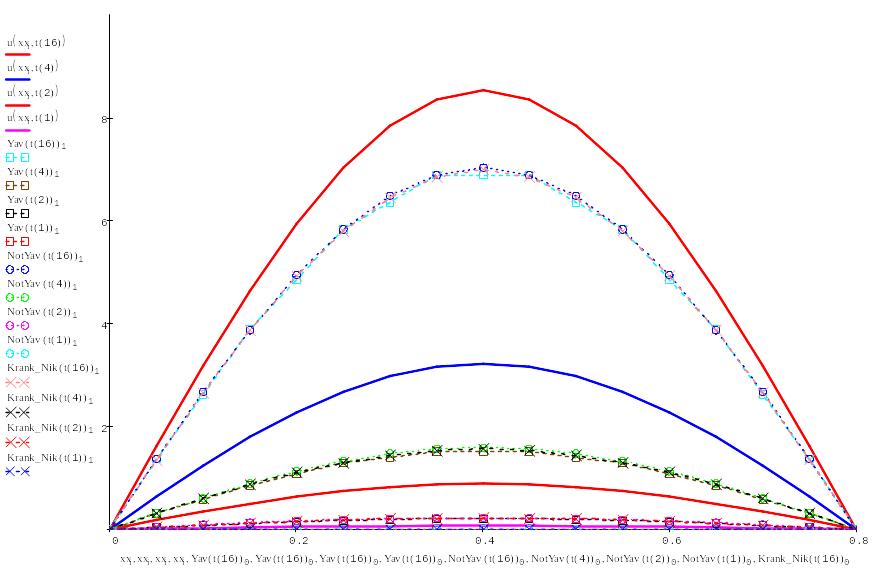
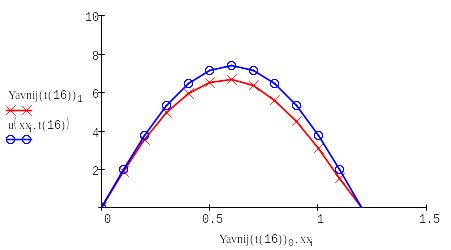
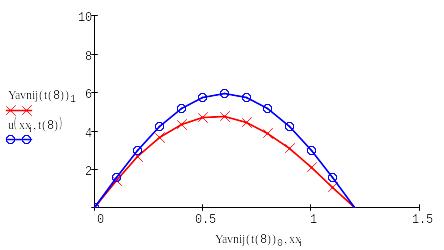
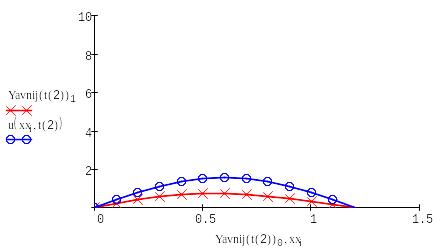
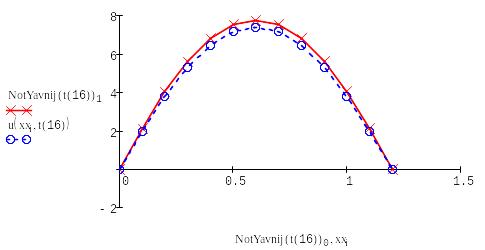
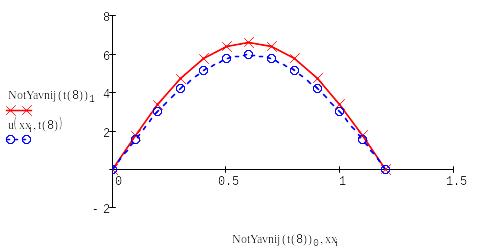
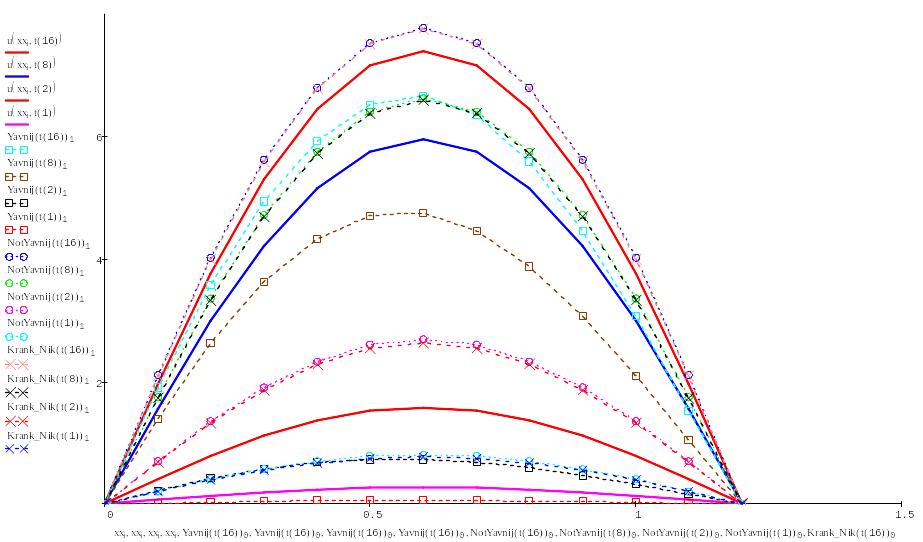
Выводим в одном графике все полученные решения:

Вывод:

Проведя лабораторную работу, мы выяснили, что самый наиболее точные алгоритмы - основаны на схеме Кранка – Николсона и явной схеме, а самый неточный - алгоритм на основе неявной схемы.

Тексты программ: