Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Уральский федеральный университет

имени первого Президента России Б.Н.Ельцина»

Нижнетагильский технологический институт (филиал)

Департамент технологический

Кафедра "Информационных технологий"

Оценка работы

________________________

________________________

^{(Ф.И.О, подпись)}

Вычислительная математика

Отчет по лабораторной работе №1

Вариант №7

Проверила: Мартышенко Ю.Г.

Студент гр. 20123 ПОВТ Рыжков Д. Е.

Н. Тагил

2013

Оглавление:

Введение………………………………………………………………………………………………	4
Численное решение нелинейных уравнений……………………………………………………..	5
Постановка задачи 1.1…..……………………………………………………………………..	5
Теоретический материал……………………………………………………………………..	5
Результаты вычислительного эксперимента………………………………………………..	7
Вывод………………………………………………………………………………………….	9
Тексты программ……………………………………………………………………………...	9
Постановка задачи 1.2……………………………………………………………………..	11
Результаты вычислительного эксперимента………………………………………………..	11
Вывод…………………………………………………………………………………………..	12
Численное решение систем линейных уравнений прямыми методами……………………..	13
Постановка задачи 2.1……………………………………………………………………..	13
Теоретический материал……………………………………………………………………..	13
Результаты вычислительного эксперимента………………………………………………..	14
Вывод………………………………………………………………………………………….	15
Тексты программ……………………………………………………………………………...	16
Численное решение систем линейных уравнений итерационными методами….…………..	18
Постановка задачи 3.1……………………………………………………………………..	18
Теоретический материал……………………………………………………………………..	18
Результаты вычислительного эксперимента………………………………………………..	20
Вывод………………………………………………………………………………………….	21
Тексты программ……………………………………………………………………………...	21
Численное интегрирование…………………………………………………...….………………..	25
Постановка задачи 4.1……………………………………………………………………..	25
Теоретический материал………………………………………………………………………	26
Результаты вычислительного эксперимента………………………………………………..	27
Постановка задачи 4.2……………………………………………………………………..	28
Результаты вычислительного эксперимента………………………………………………..	28
Вывод…………………………………………………………………………………………..	28
Тексты программ……………………………………………………………………………….	29
Численное решение систем нелинейных уравнений	32
Постановка задачи 5.2……………………………………………………………………..	32
Теоретический материал………………………………………………………………………	32
Результаты вычислительного эксперимента………………………………………………..	36
Вывод………………………………………………………………………………………….	36
Тексты программ……………………………………………………………………………...	37
Численное решение задачи Коши для обыкновенного дифференциального уравнения….	44
Постановка задачи 6.2……………………………………………………………………..	44
Теоретический материал……………………………………………………………………..	44
Результаты вычислительного эксперимента………………………………………………..	46
Вывод………………………………………………………………………………………….	49
Тексты программ……………………………………………………………………………...	49
Приближение функции…...…………………………………………………...….………………..	51
Постановка задачи 7.1 ……………………………………………………………………..	51
Теоретический материал……………………………………………………………………..	51
Результаты вычислительного эксперимента………………………………………………..	52
Вывод………………………………………………………………………………………….	55
Тексты программ……………………………………………………………………………...	56
Постановка задачи 7.2……………………………………………………………………..	57
Теоретический материал……………………………………………………………………..	57
Результаты вычислительного эксперимента………………………………………………..	59
Вывод………………………………………………………………………………………….	61
Тексты программ……………………………………………………………………………...	61
Метод наименьших квадратов………………………………...……………...….………………..	63
Постановка задачи 8.1……………………………………………………………………..	63
Теоретический материал……………………………………………………………………..	63
Результаты вычислительного эксперимента………………………………………………..	64
Вывод………………………………………………………………………………………….	65
Тексты программ……………………………………………………………………………...	65
Численное решение краевой задачи для одномерного и неоднородного уравнения теплопроводности……………………………………………………………………………………..	66
Постановка задачи 9.1……………………………………………………………………..	66
Теоретический материал……………………………………………………………………..	66
Результаты вычислительного эксперимента………………………………………………..	69
Вывод………………………………………………………………………………………….	72
Тексты программ……………………………………………………………………………...	72
Постановка задачи 9.2……………………………………………………………………..	75
Результаты вычислительного эксперимента………………………………………………..	75
Вывод………………………………………………………………………………………….	78
Тексты программ……………………………………………………………………………...	79
Заключение…………………………………………………………………………………………….	81
Список литературы…………………………………………………………………………………	82

Введение

Вычислительная математика — это наука о методах решения вычислительных задач на компьютере. Она появилась от необходимости решать практические задачи, такие, как управление сложными технологическими процессами, управление полётом ракет, моделирование физических процессов (процесса ядерного распада, химических реакций, роста кристаллов и др.)

Задачами вычислительной математики занимались такие выдающиеся учёные, как Эйлер, Лагранж, Чебышёв, Якоби, Лежандр, фон Нейман и многие другие. Они, часто занимаясь сложными вычислениями вручную на бумаге, невольно заложили основы науки об эффективных безошибочных вычислениях на компьютерах.

Всем известно, что компьютеры имеют дело с числами с ограниченным количеством знаков после запятой. Казалось бы, какая мелочь! Однако именно эти «мелочи» могут сильно исказить результаты численных расчётов. Появился важнейший раздел вычислительной математики — теория устойчивости вычислительных методов, то есть таких методов, которые позволяют на компьютере с «неточной» арифметикой получать точные (правдивые) результаты.

Численное решение нелинейных уравнений

Постановка задачи 1.1

Дано уравнение f(х)=0.Найти с точностью до все решения заданного уравнения на интервале [a;b]. Для решения задачи использовать: метод бисекции, метод простой итерации, метод Ньютона, метод секущих, метод ложного положения и метод Стефенсона.

Теоретический материал

Рассмотрим нелинейное уравнение f (x) = 0. Корнем уравнения называется такое число с, что f (c) = 0. Корень будет простым, если f ′(c) ≠0, и кратным порядка m , если

f (k ) (c) = 0, k =1,2,...m −1. Графически простой корень соответствует точке пересечения графика функции y = f (x) с осью Оx под ненулевым углом, а кратный корень соответствует точке пересечения под нулевым углом (рис. 1).

Рис.1

Решение задачи отыскания корней нелинейного уравнения осуществляется в два этапа. Первый этап – этап отделения корней, второй этап – этап итерационного уточнения корней.

В большинстве случаев отделение корней можно провести графически. В сомнительных случаях графическое отделение корней необходимо подкрепить вычислениями. При этом используются очевидные положения:

1) если непрерывная функция принимает на концах отрезка [a,b] значения разных знаков (т.е. f (a) >0, f (b) <0), то уравнение имеет на этом отрезке по крайней мере один корень.

2) если же непрерывная функция к тому же строго монотонна, то корень на отрезке единственный.

Метод бисекции и метод простой итерации

Пусть уравнение f (x) =0 на отрезке [a,b] имеет единственное решение, причём f (x) непрерывная функция на данном отрезке. Разделим отрезок [a,b] пополам в точке

d = (a+b)/2. Если f (d) ≠0, то возможны два случая:

1) функция f (x) меняет знак на отрезке [a,d];

2) функция f (x) меняет знак на отрезке [d,b];

Выбирая в каждом случае отрезок [a n,b n], на котором функция f (x) меняет знак, и, продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения. Середина n-го отрезка – точка x n = (a n + b n ) /2 даёт приближение корню с.

|x n −c| ≤(b n −a n) / 2 =(b-a) / . (1)

Критерием окончания итерационного процесса служит неравенство

(b n −a n ) / 2 <ε.

Можно принять x n =(a n + bn) /2 за приближение к корню с точностью ε.

Метод Ньютона и его модификации

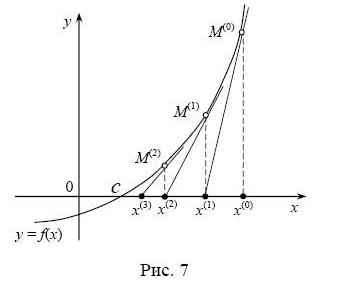
Рис.2

Пусть x0 – заданное начальное приближение к корню с. В точке М0(x0, f(x0)) проведём касательную к графику функции y = f (x) и за новое приближение x1 примем абсциссу точки пересечения этой касательной с осью Оx. За приближение x2 примем абсциссу точки пересечения с осью Оx касательной, проведённой к графику функции в точке М1(x1, f(x1)). Продолжая этот роцесс далее, получим последовательность { x n } приближений метода Ньютона к корню с.

Уравнение касательной к графику функции y = f (x) в точке Мn (xn, f(xn)) имеет вид

y = f (xn ) + f ′(xn )(x − xn ) (2)

Полагая в уравнении касательной y = 0, получим расчётную формулу для (n+1)x

метода Ньютона:

(3)

Замена в формуле (3) метода Ньютона производной приближением

₍₄₎

приводит к расчётной формуле метода секущих:

, ₍₅₎

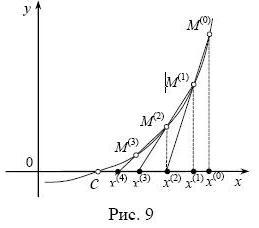
Рис.3

Замена в формуле (3) метода Ньютона производной приближением

(6)

приводит к расчётной формуле метода Стеффенсена:

₍₇₎

Для вычисления корня уравнения кратности m используют следующую модификацию метода Ньютона, сохраняющую квадратичную скорость сходимости:

₍₈₎

Замена в формуле (3) метода Ньютона производной приближением (9)

где d – фиксированная точка из окрестности простого корня, приводит к расчётной формуле метода ложного положения:

₍₁₀₎

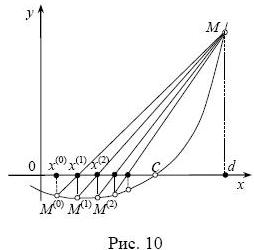
Рис.4