4.Модель петли Ньюхолла.

В петле Ньюхолла по всей петле от одного узлового интерфейса к другому передается маркер ( управляющий символ). Передавать сообщение в петлю может только тот узловой интерфейс, на который поступил маркер. Все остальные интерфейсы в этот момент могут только принимать сообщения. После завершения передачи маркер передается в следующий узел, разрешая ему начать передачу, если в узле есть сообщение для передачи. Такой протокол исключает пересечение передаваемых разными интерфейсами сообщений, т.к. в каждый момент времени активным может быть только один передатчик. При этом узловой интерфейс готовый к передаче всегда должен ждать получения маркера даже, если свободна примыкающая к узлу часть петли. Поэтому в петле Ньюхолла невозможно одновременное использование петлевого канала двумя или более передатчиком.

Среднее время реализации протокола доступа для петли Ньюхолла T_A - это время в течение которого сообщение ожидает поступление маркера. В среднем - это время равно половине интервала S – времени прохождения маркера по всему кольцу, т.е.

T_A = .

Интервал времени S в битовых единицах можно выразить в виде соотношения:

S = (6)

Где:

di - задержка распространения сигнала между i - ым и (i +1) узлами;

- величина задержки в узле;

Х - это время, в течение которого из узлов в петлю передаются все сообщения, накопленные в интервале между двумя последовательными поступлениями маркера на данный узел.Очевидно, это время равно произведению трех сомножителей:

числа узлов в петле;

числа поступивших в узлы сообщений за время сканирования;

времени обслуживания узловым интерфейсом одного сообщения.

Таким образом имеем:

Х=

Подставляя полученное выражение в (6) получим:

S= 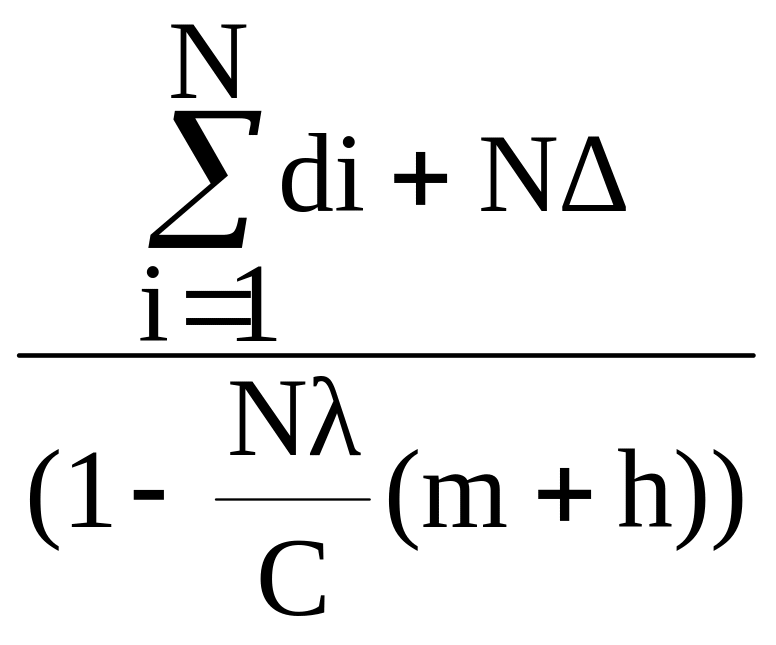(7)

В результате среднене время реализации протокола доступа Т_A определится формулой:

Т_A =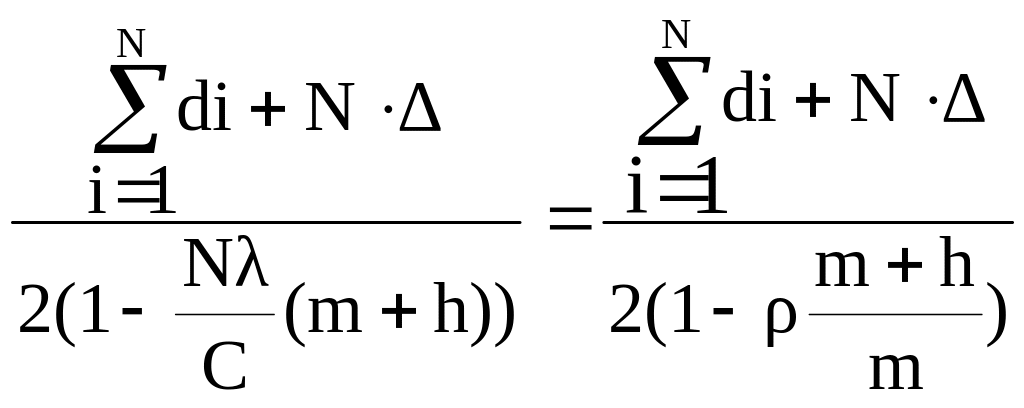 (8)

Рассмотрим, из чего складывается среднее время распространения сигнала Тр_.

Величина Тр образуется из отрезков времени движения сообщения по межузловыми каналами и задержек в узлах петли. Минимальное значение Тр принимает при передаче сообщения через один узел по одному межузловому каналу, а максимальное - через N узлов и N межузловых каналов. Поэтому среднее значение Тр будет равно:

Тр 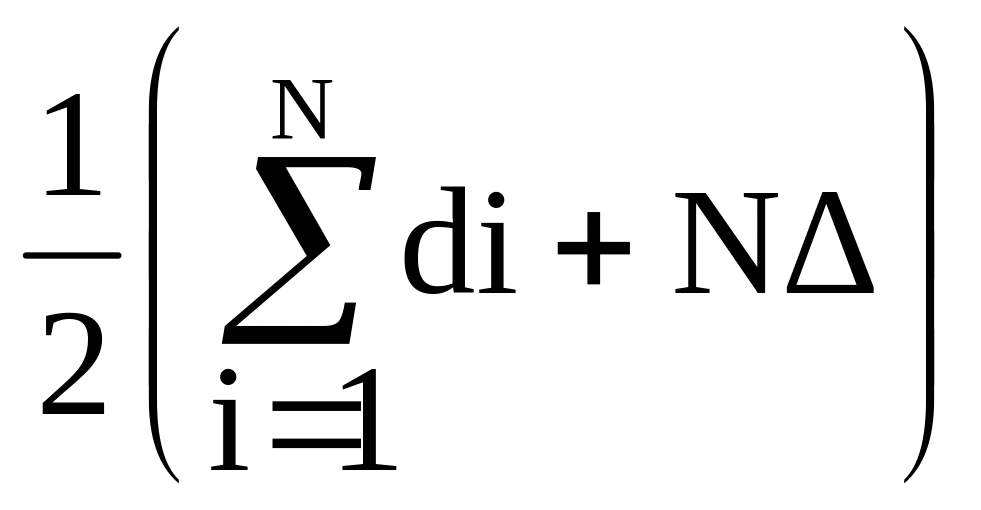₌ (9)

Подставляя в уравнение (1) величины

T_q ,T_A , T_s , T_P , определяемые формулами (5), (8), (4), (9), будем иметь:

T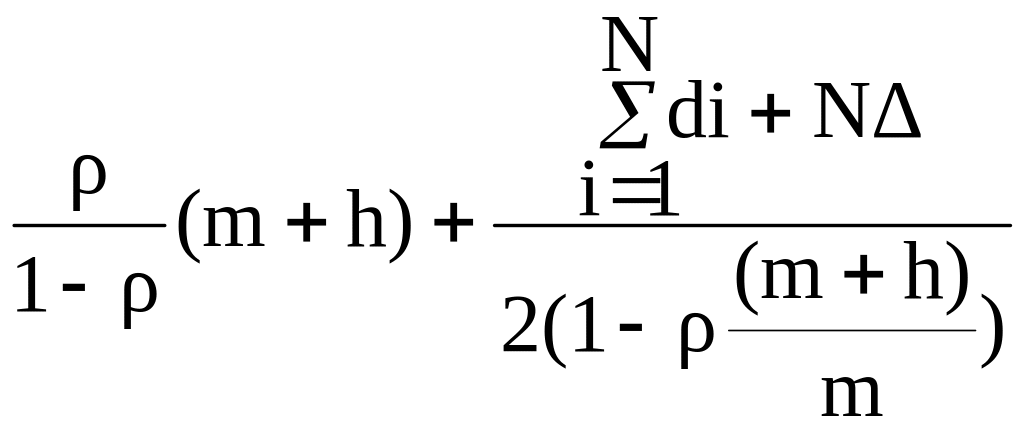_= + (m+h) + ( 10)

5.Модель петли Пирса.

В петле Пирса канал связи делится на целое число участков фиксированной длины. Эти участки петли можно сравнить с контейнерами для перемещения пакетов фиксированной длины, на которые разбивается сообщение при передаче. За каждым таким контейнером закрепляется бит управления, который определяет занятость или доступность контейнера. Любой узловой передатчик, подключенный к петле, при наличии готового к передаче сообщения должен дождаться поступления пустого контейнера и заполнить его пакетом. Каждый пакет имеет заголовок, в котором содержится адрес назначения и управляющая информация. Узловые интерфейсы выполняют следующие функции:

 автоматическую сегментацию передаваемых сообщений на пакеты с адресными признаками;

 автоматическую сборку принимаемых пакетов в исходное сообщение с удалением адреса и служебной информации;

 контроль ошибок.

После приема пакета адресуемым узлом пакет удаляется из петли и свободный контейнер перемещается к следующему узловому интерфейсу.

Пусть n - число участков-контейнеров, на которое разбивается петля и R – число заполненных контейнеров. Тогда для каждого узла вероятность того,что поступающий контейнер заполнен, будет равно R/n. Общее число узлов в петле равно N, поэтому вероятность того, что пакет из заполненного контейнера поступит на адресуемый узел будет равна R/nN

При поступлении пакета в адресуемый узел контейнер освобождается и , т.к. общее число адресуемых узлов равно N, то число очищенных контейнеров за интервал перемещения контейнера равно:

N ( R/nN) = .

В стационарном режиме работы петли количество заполняемых и очищаемых контейнеров выравнивается,поэтому величина R/n определяет среднее число передаваемых пакетов за интервал перемещения контейнера.

Текущую пропускную способность петли Пирса можно определить как общее количество переданных битов в течение интервала перемещения контейнера, т.е.

,

где

k - число бит в одном пакете;

- интервал времени перемещения одного контейнера.

В стационарном режиме суммарный входной трафик Nm становится равным текущей пропускной спасобности петли, поэтому

Nm = ,

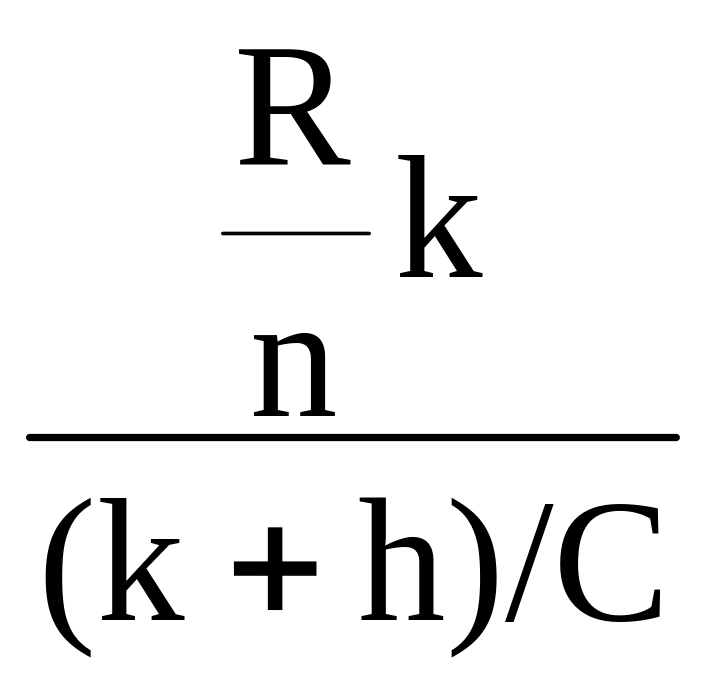а коэффициент загрузки петли Пирса будет равен  = и, т.к. отношение , то для петли Пирса можно принять ( 11).

Для определения времени доступа Т_A необходимо определить время ожидания подхода пустого контейнера к наблюдаемому узлу. Это время складывается из двух составляющих: времени синхронизации и случайного времени ожидания подхода пустого контейнера, которое зависит от случайного распределения по кольцу загруженных контейнеров.

Время синхронизации равно в среднем половине интервала перемещения одного контейнера через узел, т.е. .

Для определения второй составляющей величины Т_A напомним, что R/n и 1 - R/n – это вероятность того, что поступающий к узлу контейнер является заполненным или пустым соответственно.Если поступающее в петлю сообщения полностью помещаются в один контейнер, то вторую составляющую можно определить выражением:

(k +h)  .

Если же сообщения содержат m/k пакетов, то вторая составляющая будет равна:

,

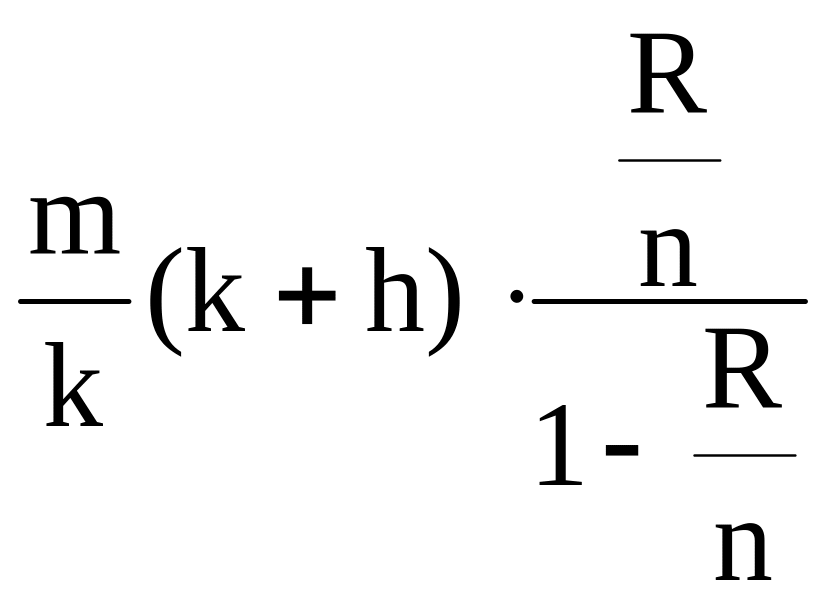где m - средняя длина сообщения в битах;

к - длина одного пакета в битах.

Следовательно, общее среднее время доступа Т_A в петле Пирса определится выражением:

Т_A =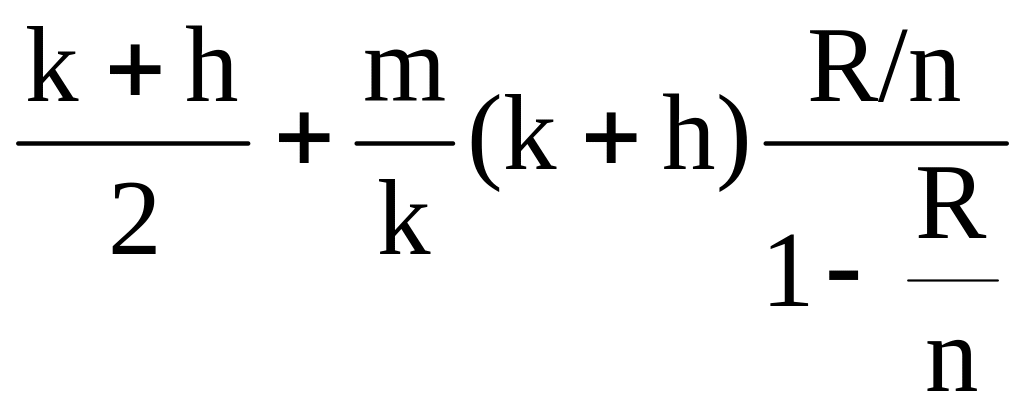 (12)

Учитывая то , что среднее время распростаренения сигнала в петле Пирса такое же ,как и в петле Ньюхолла ,можно записать выражение для Т_ , подставляя в формулу (1) уравнения (5), (12), (4), (9), и с учетом (11) получим:

Т_ = (13)

6. Модель петли Хафнера

Известны две модификации петли Хафнера [5].

Основное отличие одной модификации от другой состоит в том, что в одной из них используются сообщения переменной длины, а в другой фиксированной.Прицип действия петли Хафнера можно пояснить в помощью рис.4.

Каждый узловой интерфейс содержит два сдвиговых регистра: для приема сообщений -RSR и передачи -TSR.Передачей и приемом сообщений управляет трехпозиционный переключатель SW, который соединяет выходы регистров и входную ветвь петли с ее выходной ветвью.

Если в узле отсутствуют сообщения для передачи или пакеты в петле с фиксированной длиной сообщений, то в таком случае переключатель находится в положении 1. Как только в узле появляется сообщение для передачи, оно заносится в регистр TSR, переключатель SW переводится в положение 2 и начинается передача сообщения из региста TSR в петлю. При этом очередное сообщение, циркулирующее в петле, заносится в регистр RSR. После завершения передачи сообщения из регистра TSR переключатель переводится в положение 3 и очередное сообщение, поступившее из петли и задержанное в буферном регистре RSR, передается из регистра в петлю и затем переключатель SW переводится в положение 1. В каждом очередном сообщении из петли, поступившем в RSR, проверяются адресные признаки и при их совпадении сообщение отправляется адресату в данном узле.

В петле Хафнера суммарное время передачи сообщений также складывается из четырех отрезков времени T_q ,T_A , T_s и T_P . В этой петле величины T_q и T_s имеют такое же значение как и в петлях Ньюхолла и Пирса. Детальный анализ временных задержек T_A и T_P для петли Хафнера было выполнено в работе [ 6 ], в которой получены следующие результаты:

Ta = 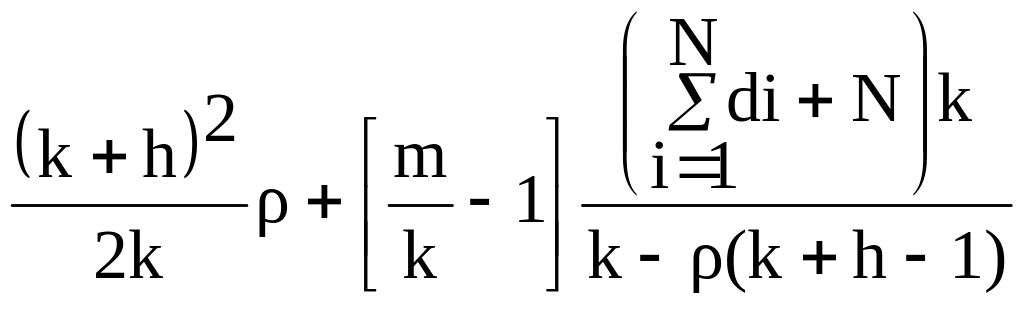(14)

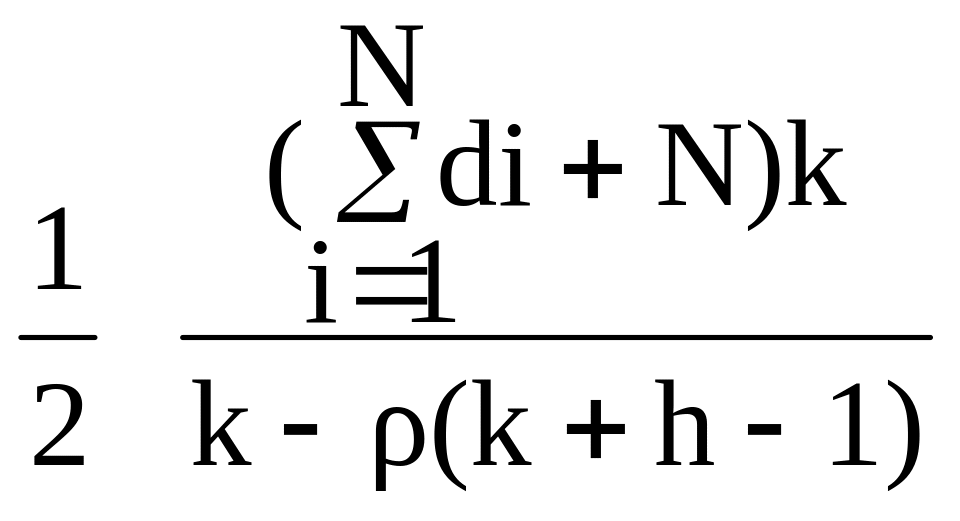Tp = (15)

Используя эти результаты можно выразить суммароное время передачи сообщений в петле Хафнера:

Т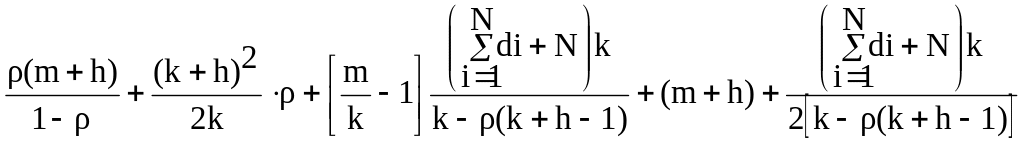_ = (16)

В модели петли Хафнера переменные k,h,m,di,, N имеют такое же значение, как и в рассмотренных выше моделях петли Ньюхолла и Пирса.