6.Сравнительный анализ надежности системы

обьектных контроллеров.

Повышение надежности системы ОК за счет внедрения программы тестирования оценим путем сравнительного анализа показателей надежности системы с применением и без применения этой программы.

С этой целью будем рассматривать систему ОК как технический обьект, который в процессе функционирования может находиться в одном из 4-ех возможных состояний:

S_o – технический обьект исправен;

S₁ – обьект неисправен, отказ в порте петли с петлевым каналом;

 S₂ – обьект неисправен из-за отказа концентратора с линиями связи контроллера;

 S₃ – обьект неисправен из-за отказа обьектного контроллера с обьектными кабелями.

Расмотрим два варианта функционирования системы обьектных контроллеров в процессе появления и устранения отказов в системе:

функционирование системы и устранение отказов без применения программы тестирования;

функционирование системы и устранение отказов с использованием программы тестирования.

6.1.Расчет вероятностей состояний системы без использования программы тестирования.

Пусть  - характеристики компонентов системы ОК имеют следующие значения:

₁= 0,5 - для порта петли с петлевыми каналами;

₂ = 0,01 - для концентратора с линиями связи контроллера;

₃ = 0,08 - для обьектного контроллера с обьектным кабелем.

Интенсивность восстановления компонентов системы без использования программы тестирования можно задать по опыту эксплуатации системы, используя статистические данные о средних затратах времени на поиск и устранение отказов в этих компонентах.

Предположим, что для локализации и устранения отказа в порте петли и петлевом канале, необходимо в среднем около 2 часов, в концентраторе с линиями связи, контроллера около 3 часов 20 минут и в обьектеном контроллере с обьектными кабелями около 2,5 часов. При таком предположении интенсивности восстановления этиих компонентов будут равны:

₁= 0,5 , ₂= 0,3 , ₃ = 0,4 .

Для принятых предположений и значений  и  граф состояний системы ОК будет иметь вид:

Т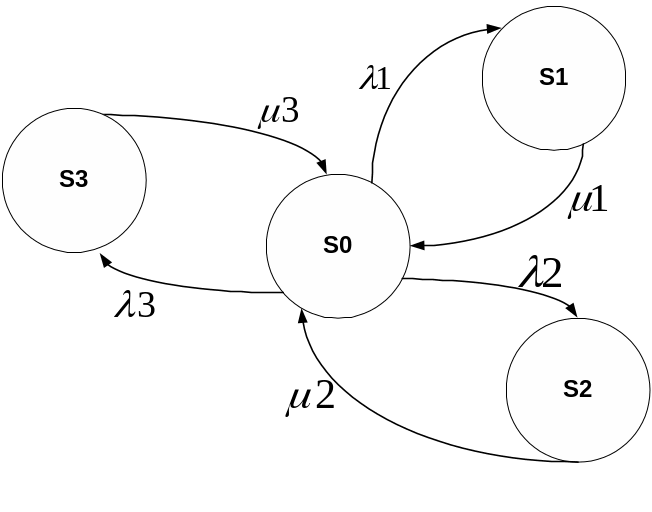 аким образом, если система исправна и находится в состоянии S_o, то из этого состояния она переходит в неисправное состояние S_1, S₂ или S₃ с интенсивностями ₁, _{2 ,} ₃ соответственно и восстанавливается, т.е. переходит из состояний S_1, S_2, S_3, в состояние S_o с интенсивностями _{1 ,} ₂, ₃ соответсвенно.Обозначим вероятности состояний S_o ,S_1, S_2, S₃ через Р_o(t), Р₁(t), Р₂(t), Р₃(t). Очевидно, для любого момента времени t должно соблюдаться равенство:

Р_o(t),+ Р₁(t), + Р₂(t)+ Р₃(t) = 1

По графу состояний составим дифференциальное уравнение Колмогорова для вероятностей состояний в соответствии с правилом, приведенным в разделе 3 главы 4 [1].

Будем иметь:

(4)

.

Эта система уравнений легко решается численным методом при начальных условиях:

P_o(0) = 1, P₁(0) = P₂(0)= Ps(0) = 0.

И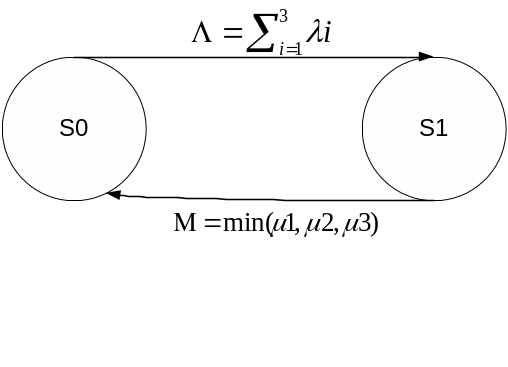 спользуя встроенную функцию rkfixed MathCADa можно получить решение системы дифференциальных уравнений.Результаты решения и график изменения во времени вероятностей состояний Р_o(t), Р₁(t), Р₂(t), Р₃(t) представлены в приложении 2.

6.2.Расчет показателей надежности системы без использования программ тестирования.

Для оценки показателей надежности цепи « напольные устройства-CTS» рассмотрим эту цепь в двух возможных состояниях:

Sо –цепь исправна;

S_{1 -} цепь неисправна независимо от того, в каком из компонентов цепи появится отказ.

В таком случае переход системы из одного состояния в другое будет определяться суммарной интенсивностью отказов и интенсивностью восстановления М, которая может принимать одно из трех возможных значений _{1 ,} ₂ или ₃ в зависимости от того, в какой из частей системы ОК появится отказ. Чтобы не завышать искомые показатели надежности примем в качестве интенсивности М наименьшую из интенсивностей восстановления компонентов цепи.

В результате граф состояний системы ОК будет иметь вид :

Обозначая вероятности состояний через Р_o(t), Р₁(t) и составляя дифференциальные уравнения Колмогорова по известному правилу будем иметь:

(5)

.

Так как для любого момента времени t соблюдается условие Р_o(t) + Р₁(t)=1, то подставляя в первое уравнение Р_{1 =} 1-Ро получим:

Решение этого уравнения в квадратурах имеет вид:

(6)

Зависимость вероятности Р_о(t) – исправного состояния системы от времени представлена на графике приложения 3. В этом же приложении приведены численные значения показателей надежности системы:

Т_о – среднего времени безотказной работы;

Кg – коэффициенты готовности системы;

P(t)

–вероятности безотказной работы системы в течение времени t.

6.3.Расчет вероятностей состояний системы при использовании программы тестирования.

Опыт эксплуатации сложных электронных систем показывает, что при отказах в системах в процессе их восстановления большая часть времени затрачивается на поиск и локализацию отказов. Программа тестирования предназначена для сокращения времени восстановления системы после появления отказа в одном из ее компонентов.

Применение программы обеспечивает сокращение времени восстановления не менее, чем 2 раза. Поэтому граф состояний системы для расчета вероятностей состояний будет идентичен графу представленному в разделе 6.1., но с другими значениями интенсивностей восстановления.Система дифференциальных уравнений Колмогорова будет отлична от системы дифференциальных уравнений (4) только тем, что в этом случае значения интенсивностей _{1 ,} ₂ , ₃ будет выше в 2 раза.

Результаты решения новой системы дифференциальных уравнений численным методом и график зависимости вероятностей состояний Р_о(t), Р₂(t), Р₃(t) от времени представлены в приложении 4.

Сравнение численных значений вероятностей исправного состояния системы в таблицах приложений 2 и 3 свидетельствуют о том, что при использовании программы тестирования вероятность безотказного состояния существенно возрастает. Так,например, без использования программы тестирования Р_о(9)=0,453, а с применением программы Р_о(9)=0,619,причем, с увеличением t разрыв в приросте вероятности безотказного состояния увеличивается.

6.4.Расчте показателей надежности системы при использовании программы тестирования.

Для оценки показателей надежности системы ОК , в которой применяется программа тестирования, необходимо использовать методику, аналогичную изложенной в разделе 6.2.

Принимая предложения и допущения аналогичные,принятым в разделе 6.2., можно построить граф состояний системы, составить систему дифференциальных уравнений Колмогорова и получить решение этой системы в квадратурах. В результате получим формулу , выражающую зависимость вероятности исправного состояния системы от времени, аналогичную формуле (6).Отличие будет заключаться лишь в том, что значение величины М-интенсивности восстановления системы в этой формуле будет больше, чем в формуле (6).

Показатели надежности Кg, Т_о и Р(t) рассчитываются по методике, изложенной в разделе 6.2.

Результаты расчета показателей надежности и графики вероятности состояния системы

Р_о(t) и вероятности безотказной работы системы в течение времени t, представлены в приложении 5.

Анализ результатов расчетов позволяет сделать следующие выводы:

1.Программный модуль тестирования системы ОК обеспечивает сокращение времени восстановления системы при появлении отказов, в результате существенно повышается коэффициент готовности Кg системы.

2.Применение программного модуля тестирования увеличивает стационарную вероятность исправного состояния системы ОК.

3.Показатели надежности Т_о – среднее время безотказной работы и Р(t) – вероятность безотказной работы в течение времени t зависят только от параметров надежности системы объектных контроллеров и не зависят от методики поиска и устранения отказов. Поэтому эти показатели не изменяются при использовании программы тестирования.

Литература:

1.Вентцель Е.С. Исследование операций. М.Советское Радио. 1972.

2.Козлов Б.А.,Ушаков И.А.Справочник по расчету надежности радиоэлектроники и автоматики. М.Советское Радио. 1975.

П Р И Л О Ж Е Н И Е 1

Программный модуль контроля исправности СР, концентраторов, объектных контроллеров (О К) микропроцессорной централизации. Модули хранятся в памяти тестируемых устройств и выполняются для заданных чисел Х1, Х2. При выполнении модуля проверяются основные теоремы теории вычетов. rs=rsv; rp=rpv, где rs-вычет суммы чисел по модулю q ; rsv-вычет от суммы вычетов по модулю q; rp-вычет от произведения чисел по модулю q; rpv-вычет от произведения вычетов по модулю q.

Если устройства исправны , то в соответствии с теорией должны соблюдаться равенства: rs=rsv; rp=rpv. Модуль q может храниться в памяти центрального процессора, концентратора или объектного контроллера и вводиться при очередном цикле контроля программно.

#include <reg51.h>

#include <stdio.h>

int X1,X2,q,rx1,rx2,rs,rsv,rp,rpv;

int VICHET(int X, int q); Прототип функции вычисления вычетов

int main()

{ while(1){

X1=0x57; X2=0x39; q=P2; Числа Х1 , Х2 и q

rx1=VICHET( X1, q); Вычисление вычета от Х1

rx2=VICHET( X2, q); Вычисление вычета от Х2

rs=VICHET(X1+X2, q); Вычет от суммы Х1+х2

rsv=VICHET( rx1+rx2, q); Вычет от суммы вычетов

rp=VICHET(X1*X2, q); Вычет от произведения чисел Х1*Х2

rpv=VICHET(rx1*rx2, q); Вычет от произведения вычетов

TI=1;

Объектный контроллер исправен если:

1. rs=rsv, ãäå rs=r(X1+X2) rsv=(rx1+rx2);

2. rp=rpv, ãäå rp=r(x1*x2) rpv=(rx1*rx2);

if ((rs=rsv)&(rp=rpv)) Сравнение вычетов сумм и произведений.

printf(" rs=%d rsv=%d ; rp=%d rpv=%d Объектный контроллер исправен! \n",

rs,rsv,rp,rpv);

else

printf("Объектный контроллер неисправен или теория вычетов ошибочна\n");

} }

int VICHET(int X, int q) Описание функции вычисления вычетов

{

int S,A,rx ;

A=X;

while(A>=q)

{

S=A-q;

A=S;

rx=A;

};

return(rx);

}

П Р И Л О Ж Е Н И Е 2