4.Пример оределения оптимального межремонтного пробега
Целевая функция q(L)-Средние удельные суммарные затраты на проведение
плановых и неплановых ремонтов как функция пробега L и других
параметров. Необходимо найти минимальное значение этой
функции
при вариации L и фиксированных параменрах
L - Пробег;
Ch- Средние затраты на один неплановый ремонт;
1- Параметр потока отказов в период нормальной эксплуатации;
a2- Количество отказов на единицу пробега в период старения и износа;
l1 - Величина пробега к моменту завершения приработки ;
l2- Величина пробега к началу периода износа;
a1- Количество отказов на единицу пробега в период приработки;
Cp- Средние затраты на один плановый ремонт.
1 Определение производной d(q(l))/dL и приравнивание её нулю
L/Symbolics/Variabe/Differentiate
2.Решение уравнения относительно l
L/Symbolics/Variabe/Solve
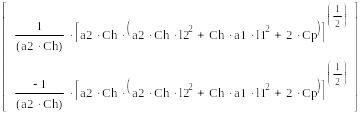
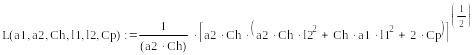
Оптимальный межремонтный пробег является функцией параметров:
a1- Количество отказов на единицу пробега в период приработки;
a2-Количество отказов на единицу пробега в период старения и износа;
Ch-Средние затраты на один неплановый ремонт;
Cp-Средние затраты на один плановый ремонт.
l1-Величина пробега к моменту завершения приработки ;
l2-Величина пробега к началу периода износа;
Для
заданных фиксированных значений
параметров
уравнение определяет
значение L при котором целевая функция q(L) имеет минимальное значение
5. Графики зависимости величины межремонтного пробега от параметров а1, а2, Сh, Cp, l1,l2.
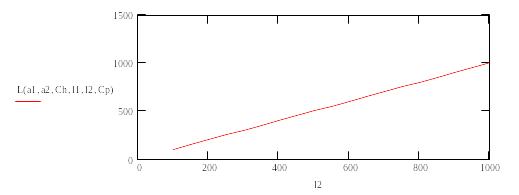
1.График
зависимости L(i2)
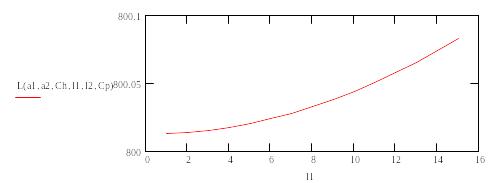
2.График
зависимости L(l1)
3.График
зависимости L(la1)
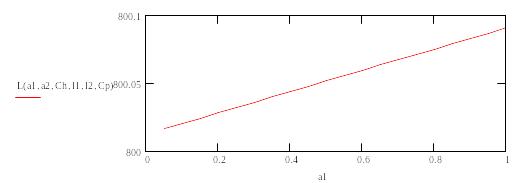
4.График
зависимости L(la2)
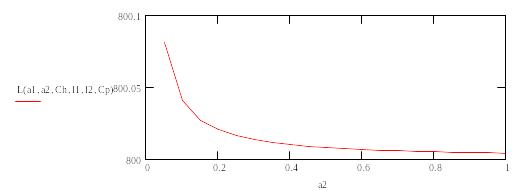
5.График
зависимости L(Ch)
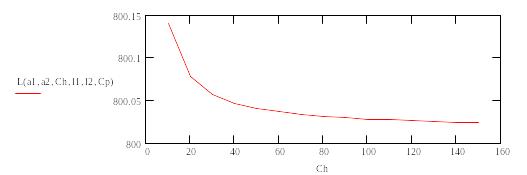
6.График зависимости L(Cp)
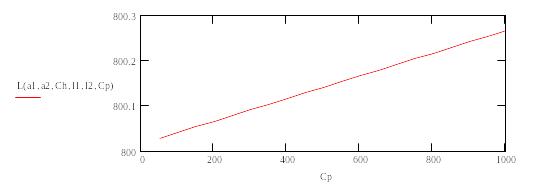
Л И Т Е Р А Т У Р А: 1ЯГУДИН Р.Ш. Надёжность устройств железнодорожной
автоматики и телемеханики. М. Транспорт, 1989.
2.ГОРСКИЙ А.В., Система ремонта ЭПС и её оптимизация. М.
МИИТ, 1991
3.ВЕНТЦЕЛЬ Е.С. Теория вероятностей. М. Наука, 1968
В.С. Любинский. Марковские модели отказоустойчивых устройств систем железнодорожной автоматики и телемеханики (сжат)
Аннотация
В статье вводится понятие отказоустойчивости устройств СЖАТ. Предлагается показатель отказоустойчивости для комплексной оценки надёжности и безопасности устройств.
Разрабатывается типовая схема отказоустойчивого устройства СЖАТ. Для оценки уровня отказоустойчивости устройств разрабатываются Марковские модели этих устройств.
Марковские модели исследуются аналитическими и численными методами с помощью программы MatchCAD и прилагаются в приложениях.
1. Введение
Задача
выбора наиболее приемлемого комплексного
показателя, характеризующего надёжность
и безопасность устройств СЖАТ, не
является тривиальной. Такая задача
рассматривается в [1], где вместе с
показателями безопасности такими как
вероятность безотказной работы,
вероятность опасного отказа, интенсивность
опасных отказов, средняя наработка на
опасный отказ предлагается комплексный
показатель – коэффициент безопасность
.
Коэффициент безопасности в [1] определяется как вероятность т ого, что система окажется в работоспособном или защитном состоянии в произвольный момент времени в процессе функционирования системы.
|
|
||
где: |
|
среднее время безопасной работы; |
|
|
|
среднее время восстановления. |
|
,
-
-
Коэффициент безопасности можно выразить через интенсивности потоков опасных отказов и восстановлений.
|
|
||
где: |
|
интенсивность опасных отказов; |
|
|
|
интенсивность восстановлений. |
|
,
-
-
Приведённая
формула для вычисления коэффициента
безопасности
отличается от известной формулы
коэффициента готовности
только тем, что в первой используется
параметр
а во второй
- интенсивность потока всех отказов.
Величины
для всех устройств СЖАТ существенно
меньше значений
,
поэтому можно утверждать, что во всех
случаях
>
.
Из этого следует, что при оценке
безопасности технических устройств
СЖАТ значение
можно рассматривать как наименьшее
граничное значение коэффициента
безопасности
.
Если найти способы приближения этой границы к своему пределу, т.е. создать устройства СЖАТ у которых значения коэффициентов готовности будут близки к единице, то для таких устройств их коэффициенты готовности могут интерпретироваться как комплексные показатели, характеризующие как надёжность, так и безопасность устройств. Подобные устройства СЖАТ с коэффициентами готовности, значения которых отличаются от единицы на пренебрежимо маленькие величины будем называть отказоустойчивыми, а их коэффициенты готовности – коэффициентами отказоустойчивости.
2. Определение отказоустойчивости технических систем
Понятие отказоустойчивости известно в технической литературе. Оно было введено в работах посвящённых исследованию надёжности специализированных вычислительных систем [2].
По определению, отказоустойчивость – это свойство системы выполнять свои основные функции при появлении отказов в аппаратных или программных компонентах системы. По способу реализации отказоустойчивость подразделяется на активную и пассивную.
Активная отказоустойчивость основана на использовании дополнительных аппаратных и программных средств позволяющих обнаружить и локализовать отказ и реконфигурировать систему так, чтобы она могла выполнять свои функции. Отказы обнаруживаются при помощи средств контроля, локализуются средствами диагностирования и устраняются автоматической реконфигурацией системы. Реконфигурация заключается в изменении структуры системы таким образом, что бы её отказавшие компоненты изолированы от исправной её части.
Пассивная отказоустойчивость заключается в свойстве системы не утрачивать свои функции в случае отказа отдельных элементов системы. Пассивная отказоустойчивость связана с увеличением объёма аппаратных средств системы и реализуется такая отказоустойчивость различными методами резервирования.
Отказоустойчивые устройства СЖАТ могут разрабатываться на основе методов пассивной отказоустойчивости с применением отдельных элементов активной отказоустойчивости. В качестве элементов активной отказоустойчивости могут использоваться средства контроля и диагностики для обнаружения и локализации отказов. Эти средства образуют дополнительную структуру обеспечивающую мониторинг текущего технического состояния устройств СЖАТ.
Применение такой структуры позволяет существенно сократить время необходимое для восстановления работоспособности устройств после появления в этих устройствах отказов.
Таким образом, исследование методов пассивной отказоустойчивости обеспечивает повышение безотказности устройств СЖАТ а применение элементов активной отказоустойчивости приводит к сокращению времени восстановления.
Оба этих фактора позволяют существенно повысить значение коэффициента готовности приближая его к единице. Из этого следует, что устройства СЖАТ, разработанные по технологии активной и пассивной отказоустойчивости обладают как высокой надёжностью, так и безопасностью.
Вместе с этим следует заметить, что разработка и применение отказоустойчивых устройств и систем
на железнодорожном транспорте основаны на безусловном соблюдении «принципа отказоустойчивости» , который применяется начиная с начального этапа развития железных дорог. Этот принцип опирается на применение компонентов с ясно определённым поведением при отказах и на то, что при отказе их части система переходит в безопасное состояние . Принцип отказоустойчивости сформулирован в Европейском стандарте EN 50126.
3. Структура отказоустойчивого устройства СЖАТ
Одним из возможных вариантов структуры отказоустойчивого устройства СЖАТ представляем на рис.1.
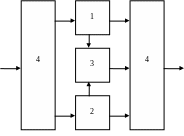
Рис.1.
Такая структура реализуется в виде дублированной системы в состав которой входят основной – 1 и дублирующий -2 функциональные блоки, блок мониторинга текущего состояния функциональных блоков – 3 и два блока 4, обеспечивающие переключение функциональных блоков по сигналам блока мониторинга.
В любой момент времени в рабочем состоянии находится один из функциональных блоков 1 или 2. Отказ в работающем блоке обнаруживается блоком мониторинга 3, сигнал о появлении отказа поступает в блоки 4, которые отключают отказавший блок и подключают резервный. Этот же сигнал используется для немедленного включения процедуры восстановления отказавшего блока.
В зависимости от значения и особенностей работы устройства СЖАТ резервные блоки могут находиться в одном из следующих режимов:
а)
Ненагруженный режим. В таком режиме
ресурс работоспособности блока,
находящегося в резерве, не расходуется.
Иными словами, если обозначить
интенсивность потока отказов в основном
работающем блоке через
,
а в резервном блоке через
,
то в ненагруженном режиме
будет иметь некоторое значение в то
время как
;
б) Нагруженный режим. В этом режиме ресурс работоспособности блока находящегося в резерве расходуется так же как и включенного в работу основного блока. В этом случае как , так и будут иметь некоторое значение и, если свойства надёжности основного и резервного блоков идентичны, то = .
г) Облегчённый режим интерпретируется как промежуточный между ненагруженным и нагруженным режимами. В этом режиме резервный блок может отказывать с некоторой интенсивностью .
Если
,
то облегчённый режим сводится к
ненагруженному, если
,
то к нагруженному.
4. Марковские модели отказоустойчивых устройств СЖАТ
Математическое описание дублированного устройства СЖАТ рис.1 можно представить в виде экспоненциальной модели. При разработке таких моделей предполагается, что время безотказной работы и время восстановления блоков моделируемого устройства подчиняются экспоненциальному расспределению.
Рассмотрим особенности математических моделей устройств СЖАТ, которые отличаются различными режимами работы резервных блоков.
4.1. Модель устройства с ненагруженным резервом.
В устройстве СЖАТ рис.1. в работающем функциональном блоке могут появляться отказы. При появлении отказа по сигналу, вырабатываемому блоком мониторинга, немедленно включается в работу резервный блок, а отказавший блок начинает восстанавливаться. В результате восстановления отказавший блок полностью восстанавливает свои свойства. Блок, находящийся в резерве, свои ресурсы работоспособности не расходует.
Время
безотказной работы функциональных
блоков подчиняется экспоненциальному
распределению с параметром
.
Длительность восстановления отказавшего
блока также подчиняется экспоненциальному
распределению с параметром
.
Необходимо разработать модель процесса
функционирования устройства для
определения вероятностей распределения
времени безотказной работы дублированного
устройства СЖАТ.
Отказ такого дублированного устройства наступает если оба функциональных блока находятся в нерабочем состоянии.
Устройство СЖАТ рис. 1 может находиться в одном из трёх возможных состояний:
-
оба функциональных блока 1 и 2 исправны;
-
один из блоков, либо основной – 1, либо
резервный – 2 неисправен;
-
оба блока 1 и 2 неисправны, т.е. состояние
- это отказ дублированного устройства.
Для
определения вероятности безотказной
работы в течение заданного времени
используем Марковскую модель в которой
состояние отказа
устройства является поглощающим [4].
В этом случае рассматриваем процесс функционирования устройства только до его отказа (когда оба блока 1 и 2 рис.1. отказали).
Система дифференциальных уравнений, описывающая случайный процесс функционирования системы:
|
(1) |
||
где: |
|
вероятность
того, что в момент времени
;
устройство находится в состоянии
|
|
,
,
,
-
,
,
соответственно
Для
начальных условий
,
,
систему дифференциальных уравнений
можно решать аналитически следуя
методике приведённой в [3].
Подставляя
из второго уравнения системы в первое,
получим:
|
(2) |
,
Аналитическое решение этого уравнения имеет вид:
|
(3) |
,
Подставляя
в первое уравнение системы (1) и решая
его относительно
имеем:
|
(4) |
,
;
.
Искомая
вероятность безотказной работы устройства
равна сумме вероятностей
и
,
т.е.
|
(5) |
После подстановки в формулу (5) , и преобразований получим:
|
(6) |
Для определения коэффициента отказоустойчивости устройства необходимо значения средних времени безотказной работы и времени восстановления.
Среднее
время восстановления
при экспоненциальном законе распределения
с параметром
равно
.
Для определения среднего времени
безотказной работы
используем известную в теории надёжности
формулу, связывающую
и вероятность безотказной работы
устройства
,
т.е.
.
После подстановки
и упрощений имеем:
|
(7) |
Из соотношения (7) следует важный для инженерной практики вывод о роли восстановления в повышении отказоустойчивости дублированных устройств. Интенсивность восстановления , обычно, значительно больше , т.е. восстановление протекает быстрее чем заканчивается период безотказной работы.
Второе
слагательное в формуле (7) представляет
собой приращение величины
за счёт восстановления. Такое увеличение
может быть значительным, а это, в свою
очередь, повышает коэффициент
отказоустойчивости
.
В приложении 1 содержаться результаты исследования модели отказоустойчивого устройства СЖАТ с ненагруженным резервом, приводятся расчёты вероятностей безотказной работы устройства, коэффициентов отказоустойчивости - и графики зависимости коэффициента от интенсивности восстановления .
Результаты расчётов свидетельствуют о высокой надёжности и безопасности предлагаемой структуры. Анализ расчётов показывает, что уровень надёжности и безопасности отказоустойчивых устройств СЖАТ существенно зависит от интенсивности восстановления.
Так
для заданных значений параметров
и
при
,
коэффициент отказоустойчивости
,
а при увеличении интенсивности
восстановления
,
.
4.2. Модель устройства с нагруженным резервом
В
этой модели предполагается, что оба
функциональных блока 1 и 2 рис.1 находятся
в рабочем режиме. В следствие этого,
интенсивность перехода из состояния
в состояние
будет равна
.
Другие условия работы устройства
аналогичны рассмотренным в 4.1.
Система дифференциальных уравнений, описывающая случайный процесс функционирования устройства, имеет вид:
|
(8) |
,
Для начальных условий , . Применяя вычислительную процедуру изложенную в [3] имеем:
|
(9) |
,
,
,
.
Вероятность безотказной работы устройства с нагруженным резервом равна сумме вероятностей и . Суммирование этих вероятностей приводит к выражению:
|
(10) |
,
Коэффициент
отказоустойчивости
определяется методом аналогичным
изложенному в §4.1. Выражаем
и
по формулам
,
и полученные выражения подставляем в
формулу
.
|
|
;
;
В
приложении
2 приведён
MatchCAD алгоритм вычисления
,
,
,
для дублированной системы СЖАТ с
нагруженным резервом. Сравнительный
анализ значений коэффициентов
для дублированных устройств СЖАТ с
ненагруженным и нагруженным резервом
показывает, что в нагруженном режиме
резерва величина коэффициента
отказоустойчивости снижается. Так, в
ненагруженном режиме резерва
,
а в нагруженном
при одинаковых для обоих режимов
значениях интенсивностей
и
.
4.3. Модель устройства с облегчённым режимом загрузки резервного блока.
В
этой модели у работающего блока
интенсивность потока отказов равна
,
а у резервного
,
при чём
<
.
Поэтому интенсивности перехода устройства
из состояния
в состояние
будет
.
Система дифференциальных уравнений, описывающая случайный процесс функционирования устройства, имеет вид:
|
(11) |
,
В
результате решения этой системы для
начальных условий
,
имеем уравнения определяющие
и
и суммировав их получим выражение для
вычисления вероятности безотказной
работы
дублированного устройства с облегчённым
режимом резервного блока.
|
(12) |
,
,
Для вычисления коэффициента отказоустойчивости определяем среднюю длительность безотказной работы устройства используя формулу .
Подставляя в эту формулу и интегрируя, получим:
|
(13) |
,
Далее находим значение по формуле:
,
|
|
В приложении 3 приведены MatchCAD алгоритмы вычисления , , и коэффициента для дублированного устройства СЖАТ с облегчённым режимом резервного функционального блока.
Сравнение
коэффициента
,
вычисленного для схемы устройства с
облегчённым режимом резерва с аналогичными
коэффициентами устройств с загруженным
и ненагруженным
резервными блоками показывает, что
величина коэффициента
устройства с облегчённым режимом резерва
занимает промежуточное положение между
величинами коэффициентов устройств с
ненагруженным и загруженным режимами,
т.е.
|
|
Так,
например, для идентичных значений
параметров
и
во всех трёх схемах устройств и значении
в схеме с облегчённым режимом коэффициенты
отказоустойчивости имеют следующие
значения:
|
|
;
;
MatchCAD алгоритм сравнительного анализа коэффициентов отказоустойчивости для трёх режимов работы резервных функциональных блоков приведена в приложении 4.
Выводы
В статье введено понятие отказоустойчивого устройства СЖАТ. Предложена структура отказоустойчивого устройства;
В качестве нормы отказоустойчивости предложен показатель – коэффициент отказоустойчивости. Коэффициент отказоустойчивости определён как комплексный показатель характеризующий безотказность и безопасность устройства СЖАТ;
Разработаны Марковские математические модели отказоустойчивых устройств СЖАТ с различными режимами работы резервных функциональных блоков.
Исследована зависимость коэффициента отказоустойчивости предложенной структуры устройства СЖАТ от режимов работы резервных функциональных блоков и параметра характеризирующего интенсивность восстановления.
Результаты расчётов:
Ненагруженный режим работы резервного блока:
,
,
Нагруженный режим работы резервного блока:
, ,
Облегчённый режим работы резервного блока:
, ,
5. Заключение
Значение коэффициента готовности технической системы равное единице - это придел надежности к которому необходимо стремиться при создании технических систем, отказ которых может привести к катастрофическим последствиям. Вместе с этим известно, что один из самых сложных вопросов в теории надежности - является выбор оправданных количественных требований по надежности на технические устройства различного назначения. Насколько обоснованной и целесообразной может быть такая норма надежности для устройств СЖАТ как значение коэффициента готовности равное единице?
Повышение надежности технических систем связано с увеличением затрат на производство этих систем, однако, при обосновании требований к норме надежности, необходимо сравнить не только затраты на производство тех или иных устройств, но и экономические потери последствий вызванных аварией или катастрофой после отказа устройства.
В системах, обеспечивающих безопасность движения поездов имеются устройства, отказ которых может привести к самым трагическим последствиям. Нормы надежности для таких устройств должны быть предельно высокими и в таких случаях проблема заключается не в стоимости изготовления этих устройств, а в том как технически такую норму обеспечить.
Предлагаемый в статье метод в создании высоконадежных устройств СЖАТ с заданными предельно высокими показателями надежности является попыткой решить проблему создания практически безотказных безопасных устройств.
Проблема создания высоконадежных отказоустойчивых систем впервые решалась применительно к специализированным компьютерным системам. Эта проблема была решена путем использования компьютерных технологий. Примером реализации отказоустойчивых компьютерных систем могут служить современные микропроцессорные системы централизации, в которых используются схемы дублирования центральных процессорных блоков.
Учитывая потенциальные возможности микропроцессорной техники можно утверждать, что схемы дублирования с автоматическим контролем технического состояния функциональных блоков применены к различным типам устройств. Применение методов активной и пассивной отказоустойчивости при создании устройств СЖАТ обеспечит высокие показатели их надежности близкие к предельно возможным значениям.
Результаты моделирования отказоустойчивого устройства, структура которого рассматривалось в статье, показывает, что даже при сравнительно низкой надежности функциональных блоков коэффициент отказоустойчивости предлагаемой структуры близок к единице, а при увеличении интенсивности восстановления становится равным единице.
Литература
Сертификация и доказательство безопасности систем железнодорожной автоматики. Под редакцией В.В.Сапожникова. М. Транспорт, 1997 г.;
Теория проектирования вычислительных машин систем и сетей. Под ред. В.И. Матова, , Москва, изд. МАИ.
B.Epstein, T.Hasford. Reliability of some two unit redundant systems. Proc. 6-th Nat. Symposium on Reliability and Quality Control, 1960 г.;
В.Козлов, И.Ушаков. Справочник по расчёту надёжности. М. Советское радио, 1975 г.