2.Критерий оптимальности периодичности ремонтов.

Для предупреждения износовых отказов оборудования ЭПС служит система планово-предупредительных ремонтов, на которых производят восстановление или замену деталей и узлов при приближении параметров, характеризующих износ детали, к предельным значениям. Назначать плановый ремонт до наступления периода износа нецелесообразно, т. к. при этом увеличивается число неплановых ремонтов за счет появления приработочных отказов.

Плановый ремонт необходимо выполнять при такой наработке L, когда параметр потока износовых отказов будет больше, чем параметр приработочных отказов [1].

Рассмотрим, как определить такие сроки проведения плановых ремонтов, чтобы суммарные затраты на проведение ремонтов, как плановых, так и неплановых ремонтов были бы минимальными. Если плановым ремонтом осуществляется плановое восстановление оборудования, то функция ( ) после планового ремонта полностью повторяет ту, которая была до его проведения. Поэтому в интервале достаточно большой наработки ЭПС зависимость ( ) будет представлять собой повторяющиеся участки кривой ( ) на интервале L, 2L, 3L .... Конец каждого интервала – это моменты завершения очередного планового ремонта. Зависимости  (L) в интервалах [0,L], [L,2L], [ 2L,3L] и т.д. полностью тождественны, поэтому для анализа достаточно рассмотреть только один интервал [0,L].

Число отказов и, следовательно, число неплановых ремонтов в интервале [0,L]

H(L) = ( 1 )

Тогда среднее число отказов ( а следовательно неплановых ремонтов) при достаточно большом пробеге :

N_H = ( 2 )

Где число плановых ремонтов в интервале [0, ].

Если средние затраты на один неплановый ремонт с учетом потерь от сбоя графика движения поездов составит С_H, а средние затраты на один плановый ремонт С_п, то суммартные затраты на проведение плановых и неплановых ремонтов будут определяться выражением:

С= С_H + С_п  ( 3 )

Разделив выражение (3). на получим средние удельные суммарные затраты на проведение плановых и неплановых ремонтов.

q (L) = [С_H + С_п ] ( 4 ).

Величина q (L) является критерием оптимальности межремонтных пробегов узлов и деталей ЭПС на основе информации об их отказах.

3.Вывод формулы оптимального межремонтного пробега .

Задачу минимизации критерия оптимальности q (L) можно решить, если будет известна функция ( ). Методом кусочно-линейной аппроксимации эту функцию можно выразить пользуясь графиком рис.1.

( 5 )

Коэффициенты ₁, _{2 –} это угловые коэффициенты, равные тангенсам углов наклона в уравнениях соответствующих прямых, т.е. _{1 = ,} _{2 = -} количество отказов на единицу пробега в период приработки и износа соответствнно.

Минимальное значение q (L) можно получить, если планово-предупредительные ремонты будут проводиться после наступления периода усиленного износа, т.е. когда L ₂ .

В таком случае интеграл в формуле (4). после подстановки аппроксимации функции ( ) (5) распадается на три:

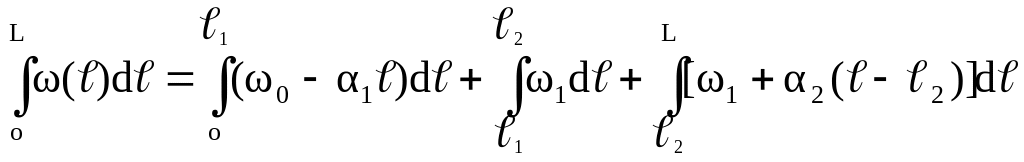( 6 )

После подстановки выражения (6). в (4). и простых преобразований имеем:

q (L) =C_н₁ + ( 7 ) .

Для определения оптимального межремонтного пробега определим точку минимума функции q(L) при вариации межремонтного пробега. С этой целью найдем производную , приравняем ее нулю и решим полученное уравнение относительно L. В результате получим новое уравнение для определения величины межремонтного пробега в зависимости от параметров _1, ₂, С_н, С_Р, ₁, ₂ . Вывод этого уравнения с использованием символического процессора MathCada представлен ниже.