Ход работы

Мгновенное значение тока в цепи с активным сопротивлением определяется по закону Ома:

i = u/r.

Если к цепи приложено переменное напряжение:

u = U_m ·sin ωt,

получим

i = (U_m /r)·sin ωt = I_m·sin ωt,

где: I_m = U_m /r – амплитуда тока.

Разделив левую и правую части на , получим закон Ома для цепи с активным сопротивлением через действующие значения напряжения и тока: I = U /r.

Сопоставление выражений для мгновенных значений напряжения и тока указывает на то, что напряжение и ток совпадают по фазе (φ = 0). Векторная диаграмма для рассматриваемой цепи показана на рис. 3.1.

Мгновенная мощность p в цепи с активным сопротивлением:

p = ui = U_m ·sin ωt· I_m·sin ωt = UI (1 – cos 2ωt).

Видно, что мгновенная мощность изменяется с удвоенной частотой и остается все время положительной. Это означает, что в цепи с активным сопротивлением мощность все время поступает из сети к потребителю r и необратимо преобразуется в тепло, нагревающее проводник и рассеивающееся в окружающей среде.

Среднее значение мощности за период находится, как: P = UI.

Эта мощность называется активной мощностью и измеряется в ваттах (Вт) или киловаттах (кВт).

2. Рассмотрим теперь цепь переменного синусоидального тока с катушкой индуктивности, активное сопротивление которой настолько мало, что им можно пренебречь.

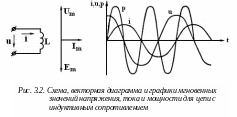
Цепь с катушкой индуктивности показана на рис. 3.2.

Будем предполагать, что ток в индуктивности изменяется по синусоидальному закону:

i = I_m·sin ωt.

Этот ток вызывает в индуктивности ЭДС самоиндукции e_L = – Ldi/dt.

В соответствии со вторым законом Киргофа

e_L= – u.

Подставив значение тока i в выражение для e_L, найдем напряжение на индуктивности:

u = L dI_m·sin ωt /dt.

Выполнив операцию дифференцирования, получим:

u = ωLI_m·sin(ωt + π /2).

Сопоставив выражения для тока и напряжения, можно сделать вывод, что ток в цепи с индуктивностью и напряжение на ней изменяются по си­нусоидальному закону и напряжение опережает ток на угол 90°. Ток, отстающий от напряжения на угол π /2, называется намагничивающим реактивным током.

Векторная диаграмма цепи с индуктивностью и графики мгновенных значений тока и напряжения показаны на рис. 3.2.

Обозначив ωLI_m = U_m, получим:

I_m = U_m /ωL.

Разделив левую и правую части последнего выражения на , получим закон Ома для цепи с индуктивным сопротивлением:

I = U /ωL = U /x_L,

где x_L = ωL= 2πfL – индуктивное сопротивление, Ом.

Мгновенная мощность p в цепи с индуктивностью:

p = ui = U_m ·sin (ωt + π /2)·I_m·sin ωt = (U_mI_m·sin2ωt) /2 = UI·sin2ωt.

Таким образом, в цепи с индуктивностью мгновенная мощность изменяется по синусоидальному закону (рис.3.2). В цепи с индуктивностью среднее значение мощности за период равно нулю, что соответствует непрерывному периодическому процессу обмена энергией между источником энергии и индуктивностью, причем в случае идеальной индуктивности потерь энергии не возникает.

Произведение UI обозначается буквой Q и называется реактивной намагничивающей мощностью. Эта мощность измеряется в вольт-ампе­рах реактивных (ВАр) и киловольт-амперах реактивных (кВАр).

3. На рис. 3.3 показана цепь переменного синусоидального тока с емкостью.

Ток в цепи с емкостью представляет собой движение зарядов к ее обкладкам:

i = dq/dt.

Учитывая, что С = q/u_c, получим:

i = С∙du_c/dt.

Напряжение на емкости изменяется по закону синуса:

u = u_c = U_m ·sin ωt.

Тогда мгновенное значение тока в цепи c емкостью:

i = С dU_m ·sin ωt /dt = ωСU_m·cos ωt = I_m·sin (ωt + π /2).

Ток в цепи с емкостью и напряжение на емкости изменяются по синусоидальному закону, но напряжение отстает по фазе от тока на угол 90°.

Векторная диаграмма цепи с емкостью и графики мгновенных значений тока и напряжения приведены на рис. 3.3.

Напряжение и ток в цепи с емкостью связаны соотношением

I_m = ωСU_m.

Разделив левую и правую части последнего выражения на , получим закон Ома для цепи с емкостью:

I = U /x_С,

где x_С =1/ωС = 1/2πfC – емкостное сопротивление, Ом.

Мгновенная мощность p в цепи с емкостью:

p = ui = U_m ·sin ωt ·I_m·sin (ωt + π /2) = (U_mI_m·sin2ωt) /2 = UI·sin2ωt.

Видно, что мгновенная мощность изменяется по закону синуса с удвоенной частотой (рис. 3.3). Среднее значение мощности за период, как и в цепи с индуктивностью, равно нулю. Следовательно, и в этой цепи происходит непрерывный периодический процесс обмена энергией между источником энергии и конденсатором, причем в случае идеального конденсатора потерь энергии не возникает.

4. Реальные электротехнические схемы могут содержать рассмотренные элементы в любом сочетании. При этом электрические цепи можно рассматривать, как совокупность разветвленных и неразветвленных участков.

Анализ таких цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. Энергетические процессы в сложной цепи можно рассматривать как совокупность процессов, происходящих отдельно в цепях с r, L, C. Одним из основных результатов анализа сложной цепи является полученное значение сдвига по фазе φ между током и напряжением.

Угол φ обычно определяют из соотношения

cos φ = U_r /U =Ir/IZ = r/ ,

где: cos φ – коэффициент мощности цепи;

r – активное сопротивление цепи;

x_L и x_C – индуктивное и емкостное сопротивления цепи, соответственно;

Z – полное сопротивление цепи.

Значение угла φ может быть получено и из треугольника сопротивлений.