Лабораторна робота № 23

Тема. МS Ехсеl. Задачi апроксимацiї й прогнозування даних. Метод найменших квадратiв. Елементи регресiйного аналiзу. Побудова лiнiй тренду на дiаграмах.

Мета. Навчитися використовувати математичнi функцiї для роботи з масивами даних i статистичнi функцiї для дослiдженяя тенденцiй (тренду) в даних.

План

1. Апроксимація. Регресійний аналіз.

2. Типи ліній тренду. Побудова лiнiй тренду

Теоретичні відомості.

1. Апроксимація. Регресійний аналіз. Для розв’язування задач про згладження експериментальних даних та апроксимацію (набли­ження) даних деякою нескладною аналітичною функцією з метою використання цієї функції для прогнозування подальших змiн даних використовують регресійний аналіз. Будь-якi експеримен­таль­ні данi можна однозначно апроксимувати лінією (функцією рівняння) – дея­кого типу прямою лінією, логарифмічною, поліноміальною чи експо­ненціальною кривою за принципом найменших квадратів – так, щоб сума квадратiв відхилень апроксимованих значень вiд експери­ментальних була мінiмальною.

Заздалегідь складно визначити, який тип функції є оптимальним для конкретних даних, зокрема, якщо їх багато. Тому якiсть апрокси­мації оцiнюють на пiдставi критерію, який називається “Критерій R-квадрат” (використовують також позначення r2). Значення r2 для рiзних функцiй буде рiзним. Апроксимація вважається тим кращою, чим ближче значення r2 до числа 1, та ідеальною, якщо r2 = 1.

Нехай у деякій однофакторнiй задачi кількість експеримен­таль­них даних п, значення фактора (незалежної величини аргументу функції утворюють масив чисел х1, х2, х3,..., хп, значення експериментальних даних утворюють масив у1, у2,..., уп. Нехай для апроксимації вибрано й визначено функцію f(x).

Тодi r2 обчислюють так:

r2 = 1 - Е/Т, де Е = Σ(у1 - f(x1))². Т = Σy²_i -(Σy_i)²/n, а суми – за iндексом i вiд 1 до п.

Найчастiше припускають, що тренд має лiнiйний характер. На основi цього вибирають функцiю f(x) = mx + b. Ріняння вигляду у = f(x) називають рiвнянням регресії. Числа m та b отримують із вхiдних даних за допомогою такого алгоритму:

1) х_с= Σ х_і/п — середнє значення фактора;

2) у_с = Σу_і/п — середнє значення експериментальних даних;

3) m = Σ (х_і — х_с)(у_і —у_с)/ Σ (х_і — х_с)²;

4) b = у_с – m × х_с.

Лінії тренду використовуються для графічного відображення тенденції даних і прогнозування їх подальших змін.

Регресійний аналіз дає змогу оцінити ступінь зв’язку між змінни­ми та прогнозувати значення певної змінної на основі відомих значень однієї або декількох інших змінних. Використовуючи регресійний аналіз, можна продовжити лінію тренду в діаграмі за межі реальних даних для передбачення майбутніх значень. Наприклад, подана нижче діаграма використовує просту лінію тренду, або лінійну апроксимацію, яка є прогнозом на чотири квартали наперед, для демонстрації тенденції збільшення прибутку.

Лінії тренду можна додати до рядів даних Кожний ряд даних на діаграмі має власний колір або інший спосіб позначення й поданий на легенді діаграми. Діаграми всіх типів, за винятком кругової, можуть містити декілька рядів даних, представлених на ненормованих плоских діаграмах з областями, лінійчаcтих діаграмах, гістограмах, графіках, біржових, точкових і булькових діаграмах. Неможливо додати лінії тренду до рядів даних на об’ємних діаграмах, нормо­ваних, пелюсткових, кругових і кільцевих діаграмах. У разі заміни типу діаграми на одну із названих вище – наприклад, якщо змінити тип діаграми на об’ємну або змінити подання звіту зведеної діаграми чи зв’язного звіту зведеної таблиці, – лінії тренду, які відповідають даним, будуть утрачені.

2. Типи ліній тренду. Є шість різних типів ліній тренду (апрокси­мація та згладжування), які можна додати до діаграми Microsoft Excel. Тип лінії тренду потрібно вибирати, виходячи з типу даних.

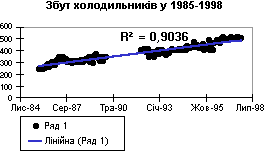
Лінійна апроксимація – це пряма лінія, яка найкраще описує сукупність даних. Її застосовують в найпростіших випад­ках, коли точки даних розміщені близько до прямої. Лінійна апрокси­мація підхо­дить для величини, яка збільшується або зменшується з постійною швидкістю.

У поданому нижче прикладі пряма лінія описує стабільне зро­стання продажу холодильників протягом 13 років. Слід звернути увагу, що R-квадрат дорівнює 0,9036, тобто близький до одиниці, що засвідчує високий ступінь збігання лінії з даними.

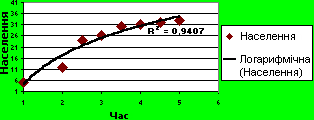
Логарифмічну апроксимацію використовують для опису величини, яка спочатку швидко зростає або зменшується, а потім поступово стабілізується. Логарифмічна апроксимація вико­ристовує як від’ємні, так і додатні значення. У наведеному нижче прикладі логарифмічна апроксимація описує прогнозоване зростання популяції тварин, які живуть в ареалі з фіксованими межами. Швид­кість зростання популяції зменшується через обмеженість їх життє­вого простору. Слід звернути увагу, що значення R-квадрат дорівнює 0,9407, що засвідчує високий ступінь збігання лінії з даними.

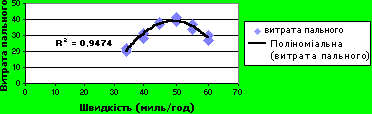
Поліноміальну апроксимацію використовують для опису вели­чин, які поперемінно зростають та зменшуються. Наприклад, її використовують для аналізу великої сукупності даних. Ступінь полінома визначається кількістю екстремумів (максимумів і міні­мумів) кривої. Поліном другого степеня може описати лише один максимум або мінімум. Поліном третього степеня має один або два екстремуми. Поліном четвертого степеня може мати не більше трьох екстремумів. У наведеному нижче прикладі поліном другого степеня (один максимум) описує залежність витрати бензину від швидкості автомобіля. Слід звернути увагу, що значення R-квадрат дорівнює 0,9474, тобто близьке до одиниці, що засвідчує високий ступінь збігання лінії з даними.

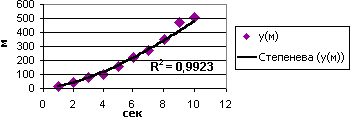
Степеневу апроксимація використовують для опису монотонно ростучої або монотонно спадної величини, наприк­лад відстані, яку проходить автомобіль під час розгону. Неможливо створити степеневу апроксимацію, якщо дані містять нульові або від’ємні значення. У наведеному нижче прикладі показано залежність відстані, яку пройшов автомобіль під час розгону, від часу. Відстань виражено в метрах, час – у секундах. Ці дані точно описано степене­вою залежністю. Слід звернути увагу, що значення R-квадрат дорівнює 0,9923, що засвідчує високий ступінь збігання лінії з даними.

Експоненційну апроксимацію використовують у тому випадку, якщо швидкість зміни даних безперервно зростає. Неможливо створити експоненційну апроксимацію, якщо дані містять нульові або від’ємні значення. У наведеному нижче прикладі експоненційна лінія тренду описує вміст радіоактивного вуглецю-14 залежно від віку органічного об’єкта. Слід звернути увагу, що значення R-квадрат дорівнює 1, що засвідчує збігання лінії з даними.

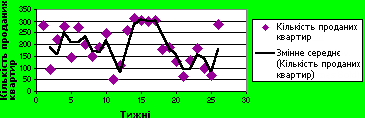
Змінне середнє згладжує відхилення в даних і чіткіше показує форму лінії тренду. Лінію будують за певним числом точок (яке визначається параметром Точки). Елементи даних усереднюють, а отриманий результат використовують як середнє значення для апроксимації. Якщо значення параметра Точки дорівнює 2, перша точка кривої визначається як середнє значення перших двох елементів даних, друга – як середнє значення наступних двох елементів і так далі. У поданому нижче прикладі показано залежність обсягу продажу протягом 26 тижнів, її отримано методом обчислення змінного середнього.

Розглянемо алгоритм додавання лінії тренду до дiаграми.

1. Побудувати дiаграму для ряду експериментальних даних.

2. Клацнути правою клавішею на маркері ряду даних, для яких потрібно побудувати лінію тренду – отримаємо контекстне меню ряду даних.

3. Виконати команду Добавить линию тренда.

4. На закладці Тип вибрати тип лінії тренду.

5. На закладці Параметры задати назву кривої (можна не задавати), довжину відрізка (в одиницях зміни аргументу) прогнозу, координату точки перетину з вiссю У (можна не задавати) зобразити рiвняння регресії на дiаграмі, розмістити на дiаграмi значения г2.

6. Натиснути ОК.