2. Модели развития операций по схеме простых процентов

Литература: 1[гл.2,§2.1], 2 [гл.2,§2.1.1]

В условиях рыночной экономики существуют различные ва­рианты инвестирования. В простейшем случае кредитор и заем­щик договариваются о величине кредита Р (первоначальная денеж­ная сумма), размере годовой процентной ставки (i%), сроке кре­дита и длительности периода(n) начисления процентов. Математи­чески такая операция может быть представлена в виде сетевой модели простых процентов. По этой модели происходит накопле­ние общей суммы долга S за счет периодического, например еже­годного, начисления процентных денег (I).

Процентная сумма определяется по формуле:

I = Pn· = Pn·i,

где i — относительная величина годовой ставки ссудного процента:

i = .

Модель накопления капитала по схеме простых процентов принимает вид

S = P + n·P·i = P·(l + n·i).

Если параметр п является дробным, то

n = ,

где t – продолжительность периода начисления процентов в днях;

Т – количество дней в году (360, 365, 366).

Тогда приведенную модель можно записать в другом виде:

S = P .

Пользуясь этой моделью, можно определять различные показатели операции:

• величину первоначальной (математическое дисконтирова­ние) суммы -

P = = ;

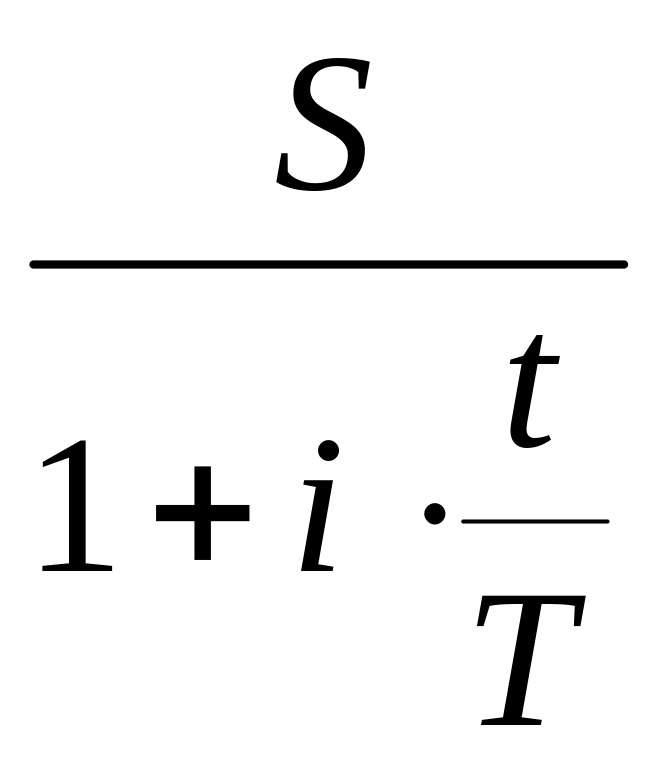• относительную величину процентной ставки –

i = = · ;

• продолжительность года –

Т = ;

• количество интервалов начисления (лет) –

n = ;

• период начисления процентов (дней) –

t = Т· ;

• коэффициент наращения по простой процентной ставке –

k_н = = (1 + i·n).

Если на последовательных интервалах начисления про­центов п_1, п_2, п_3, …, п_т, устанавливаются разные ставки про­центов i₁, i_2, i₃,…, i_m, то сумма процентных денег составит:

S = P(l + ) = P·k_н.

Коэффициент наращения равен:

k_н = 1 + .

Следует заметить, что в этом случае проценты начисляются всегда от величины первоначальной суммы Р.

Пример 2.1. Вклад 300 т.р. был положен в банк 20.05 при ставке 5% годовых. С 1 сентября того же года банк повысил ставку по вкла­дам до 6% годовых. 25 октября вклад был закрыт. Год невисокосный.

Определите сумму начисленных процентов и наращенную сумму при английской, немецкой и французской практиках начисления.

Дано: P = 300т.р., i₁ =0,05, i₂ =0,06, t₁ - c 20.05 по 1.09, t₂ - 1.09 по 25.10.

Найти: I.

Решение.

1. При немецкой практике количество дней для начисления процентов по ставке 5% годовых равно: t_н1 = (30-20) + 30∙3 + 1 = 101 дням по ставке 6% годовых: t_н2 = (30-1) + 25 = 54 дням, Т = 360.

Сумма начисленных процентов составит:

I = P · i₁+ P ·i_2.

I = 300 = 6,908334 т.р. =6908р.33к.

Наращенная сумма составит:

S = P = Р + I,

S = 300 + 6,908334 = 306,908334 т.р. = 306908 р.33к.

2. При французской практике количество дней для начисле­ния процентов (табл.1.Приложения1) по ставке 5% годовых равно:

20.05 – 140 день года, 1.09 – 244день года,

t_ф1 = 244 -140 = 104 дням;

по ставке 6% годовых равно: 25.10. - 298 день года,

t_ф2 = 298 - 244 = 54 дням. Т = 360.

Сумма начисленных процентов, вычисленная по той же формуле составит:

I = 300 = 7,033333 т.р. = 703р. 33к.

S = 300 +7,033333 = 307,033333 т.р. = 307,033333 т.р = 307033р.33к.

3. При английской практике количество дней для начисления процентов (см. таблицу Приложения1) по ставке 5% годовых равно: t_а1 = 104 дням;

по ставке 6% годовых равно: t_а2 = 54 дням. Т = 365.

Сумма начисленных процентов составит:

I = 300 = 6,936986т.р. = 6936р.99 к.

S = 300 + 6, 936986 = 306, 936986 т.р. = 309369 р. 86к.

Пример 2.2. Начисление процентов на сумму срочного депозита.

Банк 02.07 принял в межбанковский депозит денежные сред­ства в сумме 100 т.р. сроком на 7 дней по ставке 20% . Какова возвращаемая сумма? Т = 365

Дано: P = 100т.р., i_% = 20%, t = 7, Т = 365.

Найти: S.

Решение.

Банк возвращает сумму депозита с начисленными процентами 09.07 в сумме:

S = 100 · =100,38356 т.р. = 100383р.56к.

Вопросы к теме:

1. Что понимают под процентными деньгами?

2. Что понимают под процентной ставкой?

3. Модель расчета по схеме простых процентов с постоянной ставкой.

4. Модель расчета по схеме простых процентов с переменной ставкой.

5. Что понимают под наращенной суммой?

6. Что такое коэффициент наращения?