Лабораторное занятие №1.

Исследование условного и безусловного алгоритмов диагностирования по диагностической ценности признаков

Целью работы является определение информационной ценности диагностических признаков, характеризующих техническое состояние объекта и построение безусловного и условного алгоритмов диагностирования.

1.1. Краткие теоретические сведения.

В технической диагностике большое значение имеет описание объекта в системе признаков, обладающих большой диагностической ценностью. Использование неинформативных признаков не только оказывается бесполезным, но и снижает эффективность самого процесса диагностирования, создавая помехи при распознавании.

Количественное определение диагностической ценности признаков и комплексов признаков может быть приведено на основе теории информации. Главный принцип, используемый в дальнейшем – диагностическая ценность признака определяется информацией, которая вносится признаком в систему состояний.

Пусть имеется система , которая находится в одном из n возможных состояний (i=1, 2, …, n). Такая система – «система диагнозов», а каждое из состояний – диагноз. Распознавание состояний системы осуществляется путем наблюдения за другой, описанной с ней системой – системой признаков.

Назовем простым признаком результат обследования, который может быть выражен одним из двух символов или диагностическим числом (например, 1 и 0; «да» и «нет», + и – и т.п.)_.

С точки зрения теории информации простой признак можно рассматривать как систему, имеющую одно из двух возможных состояний. Если – простой признак, то два его состояния будут обозначать: – наличие признака, - отсутствие признака. Простой признак может обозначать наличие или отсутствие измеряемого параметра в определенном интервале; он может иметь и качественный характер (например, положительный или отрицательный результат испытаний и т.п.).

Если в результате обследования выявлено, что признак имеет для данного объекта значение , то это значение называется реализацией признака .

В качестве диагностического веса реализации признака для диагноза может быть принята величина:

; (1)

где – вероятность диагноза при условии, что признак получил значение , – априорная вероятность диагноза.

С точки зрения теории информации величина представляет собой информацию о состоянии , которой обладает состояние признака . Если вероятность состояния после того, как стало известно, что признак имеет реализацию в интервале S, увеличилась , то >0, т.е. диагностический вес данного интервала признака для данного диагноза положителен.

Если наличие параметра в интервале S не изменяет вероятности диагноза, то =0, так как , кроме того, диагностический интервал S признака по отношению к диагнозу может быть отрицательным (отрицание диагноза).

С учетом тождества:

,

выражение (1) можно быть представлено в виде более удобном для конкретных вычислений:

_; (2)

где – вероятность появления интервала S признака для объектов с

диагнозом ; – вероятность появления этого интервала у всех объектов с различными диагнозами.

Диагностический вес отсутствия признака в соответствии с формулой (2) определяется выражением:

_;

Так как существуют известные соотношения:

;

;

то

Диагностические веса и всегда имеют разные знаки. Кроме того, если признак является случайным для данного диагноза , то оба диагностических веса равны нулю.

Диагностический вес той или иной реализации признака еще не дает представления о диагностической ценности обследования по данному признаку. Так, при обследовании по простому признаку может оказаться, что его наличие не имеет диагностического веса, тогда как его отсутствие чрезвычайно важно для установления диагноза.

Для более объективной оценки значимости того или иного признака для установления конкретного диагноза или системы диагнозов вводится понятие диагностической ценности обследования.

Известно, что диагностическая ценность обследования по признаку для диагноза есть величина информации, вносимая всеми реализациями признака в установление диагноза .

Для m – разрядного признака:

Диагностическая ценность обследования учитывает все возможные реализации признака и представляет собой математическое ожидание величины информации, вносимой отдельными реализациями. Так как величина относится только к одному диагнозу , то это частная диагностическая ценность обследования по признаку _, и она определяет независимую диагностическую ценность обследования. Значение характерно для случая, когда обследование производится первым или когда результаты других обследований неизвестны.

Величина может быть записана в трех эквивалентных формулах:

;

;

.

Диагностическая ценность обследования для простого признака:

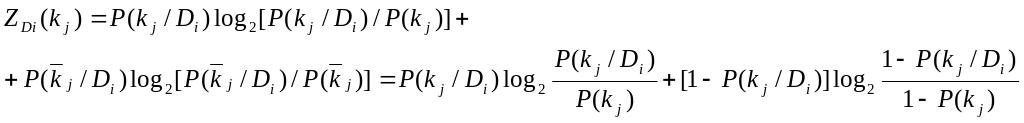
Если признак является случайным для диагноза , т.е. , то обследование по такому признаку не имеет диагностической ценности ( =0).

Наибольшую диагностическую ценность имеют обследования по признакам, которые часто встречаются при данном диагнозе, а вообще редко и, наоборот, по признакам, встречающимся при данном диагнозе редко, а вообще – часто. При совпадении и обследование не имеет никакой диагностической ценности.

Диагностическая ценность обследования вычисляется в единицах информации (двоичных единицах или битах) и не может быть отрицательной величиной. Это понятно из логических соображений: информация, полученная при обследовании, не может «ухудшить» процесс распознавания действительного состояния.

Известно, что обследование, обладающее небольшой диагностической ценностью для одного диагноза может иметь значительную ценность для другого. Поэтому целесообразно ввести понятие общей диагностической ценности обследования по признаку для всей системы диагнозов D, определив ее как количество информации, вносимое обследованием в систему диагнозов:

.

Величина представляет собой ожидаемое (среднее) значение информации, которое может быть внесено обследованием в установление неизвестного заранее диагноза, принадлежащего рассматриваемой системе (совокупности) диагнозов.

С учетом информационной ценности признаков может быть построен алгоритм определения состояния (диагностирования) объекта, представляющий собой определенную последовательность проверок признаков. Алгоритм диагностирования может быть как безусловным (не учитывающим информацию о состоянии объекта получаемую в ходе проверки каждого признака), так и условным, учитывающим приращение информации о состоянии объекта после каждой проверки очередного признака. Если выполнение алгоритма диагностирования останавливается после однозначного установления состояния объекта, то такой алгоритм называется алгоритмом с условной остановкой.

Безусловный алгоритм с условной остановкой представляется в виде графа. Корневая вершина графа представляет множество ={ } всех рассматриваемых состояний объекта, а остальные вершины – подмножества состояний, выделяемые в ходе деления множества на его подмножества, по результатам элементарных проверок. Алгоритм предусматривает выполнение элементарных проверок в определенной последовательности, которая может быть остановлена на любом этапе, если выделилось подмножество состояний соответствующее висячей вершине. На первом этапе алгоритма при проверке диагностического признака (выполнении первой проверки) получение результата 0 останавливает алгоритм, так как выделяется подмножество (рис. 1). В противном случае проверяется параметр (выполняется вторая проверка) и диагностирование продолжается.

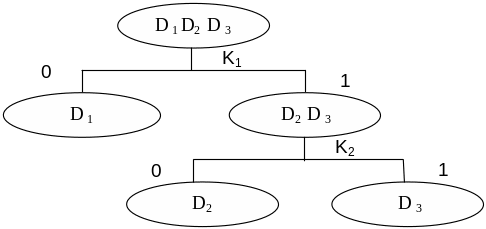
Рис.1. Безусловный алгоритм с условной остановкой.

В задачах диагностики существенным оказывается выбор наиболее информативных признаков для описания объекта. Во многих случаях это связано с трудностью получения самой информации (число датчиков, характеризующих рабочий процесс объекта, как правило, всегда ограничен). В других случаях может иметь значения время и стоимость диагностического обследования и т.п.

Для построения диагностического процесса следует учитывать сложность получения соответствующей информации. Она может быть учтена в значении коэффициента оптимальности диагностического обследования по признаку , определяемого выражением:

где – общая диагностическая ценность обследования по признаку ; – коэффициент сложности обследования по признаку , характеризующий трудоемкость и стоимость обследования, его достоверность, длительность и другие факторы.

Считается, что не зависит от проведенных ранее обследований. В этом случае последовательность выполняемых проверок в алгоритме зависит от величины коэффициента оптимальности. В качестве первого обследования принимается обследование с наибольшим коэффициентом оптимальности:

.

Вторым назначается обследование, дающее максимум:

;

и т. д.

Для алгоритма приведенного на рис.2 значение коэффициента оптимальности обследования по признаку имеет большее значение по сравнению со значением коэффициента для признака , поэтому первым выполняется обследование по признаку и лишь потом, при его единичной реализации ( ), выполняется обследование по признаку .

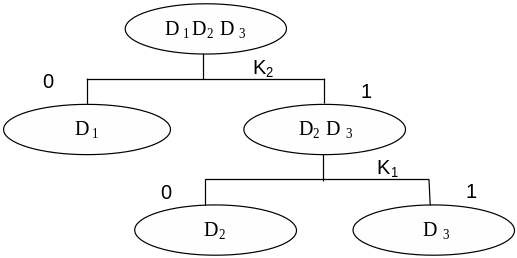
Рис. 2. Безусловный алгоритм с условной остановкой с учетом значения коэффициента оптимальности обследования.

Однако диагностическое значение признака, при последовательном обследовании, во многих случаях зависит от того, какие реализации признаков получились в предыдущих обследованиях. Бывает, что сам по себе признак не имеет существенного значения, но его появление после некоторого другого позволяет однозначно поставить диагноз (установить состояние системы). В этом случае информационная ценность признаков может быть определена следующим образом.

Пусть проводится обследование сначала по признаку , а затем по признаку . При обследовании объекта по признаку , была получена реализация , и требуется определить диагностический вес реализации признака для диагноза . В соответствии с определением диагностического веса условный диагностический вес реализации признака может быть найден из выражения:

. (3)

Независимый диагностический вес этой реализации определяется по выражению (2). Если признаки и являются независимыми для всей совокупности объектов с различными диагнозами:

,

и условно - независимыми для объектов с диагнозом

,

то условный и независимый диагностические веса реализации совпадают.

Общая диагностическая ценность обследования по признаку при условии, что результаты обследования по признаку известны (признак получил реализацию ), с учетом всех возможных реализаций признака может быть найдена по выражению:

.

В более удобном виде выражение, определяющее значение общей диагностической ценности может быть представлено:

Полученное равенство может быть записано в виде:

где частная условная диагностическая ценность обследования по признаку для диагноза определяется выражением:

.

Вид условного алгоритма с условной остановкой не отличается от безусловного алгоритма с условной остановкой, с той разницей, что первым выполняется обследование по признакам, имеющим максимальную условную ценность.