6. Масса инертная и гравитационная.

Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массывзвешиванием в современной метрологии, и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.

Инертная масса, которая характеризует меру инертности тел и фигурирует во втором законе Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу. 7. Центр масс системы материальных точек.

Центр масс (центр ине́рции; барице́нтр от др.-греч. βαρύς «тяжёлый» и κέντρον «центр») в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.

Определение

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

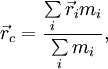
где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

Для случая непрерывного распределения масс:

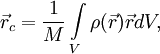
где:

 — суммарная масса системы,

 — объём,

 — плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

8. Векторы моментов силы и момента импульса.

9. Уравнение моментов. Закон сохранения момента импульса.

Производная момента импульса относительно некоторой оси по времени равна моменту действующей на материальную точку силы относительно той же оси .

(3.2)

Здесь L- момент импульса твердого тела относительно некоторой точки,   - суммарный момент внешних сил относительно той же самой точки.

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем. 10. Условия равновесия твердого тела. Примеры.

Статикой называется раздел механики, изучающий условия равновесия тел.

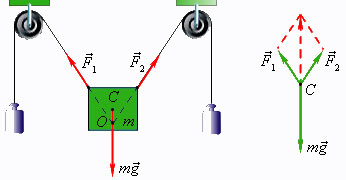
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. 

Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приведены к одной точке C.  На рис. дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.

Второе условие равновесия твердого тела

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.

Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.

Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Произведение модуля силы на плечо d называетсямоментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой трелки

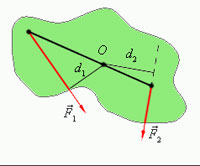  Силы, действующие на рычаг, и их моменты.  M1 = F1 · d1 > 0; M2 = – F2 · d2 < 0.  При равновесии M1 + M2 = 0.

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

M1 + M2 + ... = 0.  В Международной системе единиц (СИ) моменты сил измеряются в ньютон-метрах (Н•м).