56. Экспериментальные подтверждения кривизны пространства и замедления времени.

57. Эквивалентность массы и энергии.

Эквивале́нтность ма́ссы и эне́ргии — физическая концепция, согласно котороймасса тела является мерой энергии, заключённой в нём. Энергия тела равна массе тела, умноженной на размерный множитель квадрата скорости света в вакууме:

,

где E — энергия тела, m — его масса, c — скорость света в вакууме, равная 299 792 458 м/с.

Данная концепция может быть интерпретирована двояко:

• с одной стороны, концепция означает, что масса неподвижного тела (так называемая масса покоя) является мерой внутренней энергии этого тела^[1];

• с другой стороны, можно утверждать, что любому виду энергии соответствует некая масса. Например, было введено понятие релятивистской массы как характеристики кинетической энергии движущегося тела^[2].

В современной теоретической физике концепцию эквивалентности массы и энергии обычно используют в первом смысле^[3]. Главной причиной, почему приписывание массы любому виду энергии считается неудачным, является следующая из этого полная синонимичность понятий массы и энергии.

Масса покоя как вид энергии

Исторически принцип эквивалентности массы и энергии был впервые сформулирован в своей окончательной форме при построенииспециальной теории относительности А. Эйнштейном. Им было показано, что для свободно движущейся релятивистской частицы (а также тела и вообще любой системы частиц) выполняются следующие соотношения^[5]:

где E,  ,  , m — энергия, импульс, скорость и масса покоя частицы соответственно, c — скорость света. Из этих выражений видно, что в релятивистской механике, даже когда обращаются в нуль скорость и импульс массивного тела, его энергия в нуль не обращается^[6], оставаясь равной некоторой величине, определяемой массой тела:

Эта величина носит название энергии покоя^[7], и данное выражение устанавливает эквивалентность массы тела этой энергии. Таким образом, Эйнштейном был сделан вывод, что масса тела является одной из форм энергии^[1], тем самым законы сохранения массы иэнергии были объединены в один закон сохранения^[8].

Энергия и импульс тела являются компонентами 4-вектора энергии-импульса^[9] и соответствующим образом преобразуются при переходе из одной системы отсчёта в другую, а масса тела является лоренц-инвариантом, оставаясь при переходе в другие системы отсчёта постоянной и имея смысл модуля вектора 4-импульса.

Следует также отметить, что несмотря на то, что энергия и импульс частиц аддитивны^[10], то есть для системы частиц имеем:

масса частиц аддитивной не является^[5]. То есть масса системы частиц, в общем случае, не равна сумме масс составляющих её частиц.

Понятие релятивистской массы

После того, как Эйнштейн предложил принцип эквивалентности массы и энергии, стало очевидно, что понятие массы может использоваться двояко. С одной стороны, это та масса, которая фигурирует в классической физике, с другой — можно ввести так называемую релятивистскую массу как меру полной (включая кинетическую) энергии тела^[2]. Эти две массы связаны между собой соотношением:

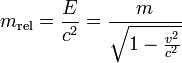
где m_rel — релятивистская масса, m — «классическая» масса (равная массе покоящегося тела), v — скорость тела. Введённая таким образом релятивистская масса является коэффициентом пропорциональности между импульсом и скоростью тела^[2]:

Аналогичное соотношение выполняется для классических импульса и массы, что также приводится как аргумент в пользу введения понятия релятивистской массы. Введённая таким образом релятивистская масса в дальнейшем привела к тезису, что масса тела зависит от скорости его движения^[11].

В процессе создания теории относительности обсуждались понятия продольной и поперечной массы частицы. Пусть сила, действующая на частицу, равна скорости изменения релятивистского импульса. Тогда связь силы   и ускорения  существенно изменяется по сравнению с классической механикой:

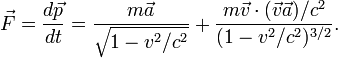
Если скорость перпендикулярна силе, то  , а если параллельна, то  , где   — релятивистский фактор. Поэтому mγ = m_rel называют продольной массой, а mγ³ — поперечной.

Утверждение о том, что масса зависит от скорости, вошло во многие учебные курсы и в силу своей парадоксальности приобрело широкую известность среди неспециалистов. Однако в современной физике избегают использовать термин «релятивистская масса», используя вместо него понятие энергии, а под термином «масса» понимая массу покоя. В частности, выделяются следующие недостатки введения термина «релятивистская масса»^[3]:

• неинвариантность релятивистской массы относительно преобразований Лоренца;

• синонимичность понятий энергия и релятивистская масса, и, как следствие, избыточность введения нового термина;

• наличие различных по величине продольной и поперечной релятивистских масс и невозможность единообразной записи аналогавторого закона Ньютона в виде

• методологические сложности преподавания специальной теории относительности, наличие специальных правил, когда и как следует пользоваться понятием «релятивистская масса» во избежание ошибок;

• путаница в терминах «масса», «масса покоя» и «релятивистская масса»: часть источников просто массой называют одно, часть — другое.

Несмотря на указанные недостатки, понятие релятивистской массы используется и в учебной^[12], и в научной литературе. Следует, правда, отметить, что в научных статьях понятие релятивистской массы используется по большей части только при качественных рассуждениях как синоним увеличения инертности частицы, движущейся с околосветовой скоростью.