53. Сокращение длины и замедление времени.

См. предыдыд. 54. Понятие интервала в теории относительности. Пространственноподобный и времениподобный интервал.

Интервал в теории относительности — расстояние между двумя событиями в пространстве-времени, являющееся обобщением евклидового расстояния между двумя точками

Квадрат интервала — это симметричная билинейная форма на конфигурационном 4-хмерном многообразии пространства-времени. При должным образом выбранных координатах (локально инерциальная система отсчета с декартовыми пространственными координатами   и временем  ) для бесконечно малого смещения в пространстве-времени он имеет вид:

(локально псевдоевклидово пространство-время, пространство Минковского в главном порядке, иначе говоря — многообразие с индефинитной псевдоримановой метрикой сигнатуры (±--)).

В случае плоского пространства-времени — то есть пространства времени без кривизны, к которому в современной физике относится случай отсутствия (или пренебрежимой малости) гравитации — такое же выражение имеет место и для конечных разностей координат:

(такое пространство уже точно и глобально является пространством Минковского, если, конечно, топологически оно эквивалентно  в своей естественной топологии).

Обычно интервал обозначается латинской буквой  .

В общей теории относительности используется обобщённое понятие интервала, дающее естественное обобщение расстояния между двумя точками. Вводится метрический тензор g_ik, от которого требуется лишь симметричность и невырожденность. Выражение для квадрата интервала между двумя бесконечно близкими точками приобретает вид:

,

где dxⁱ — дифференциалы координат, по повторяющимся индексам подразумевается суммирование, то есть это выражение означает

.

Обратим внимание, что таким образом определённая метрика не будет положительно определённой квадратичной формой, как обычно требуется (то есть как в случае собственно римановых многообразий). Напротив, подразумевается, что всегда или почти всегда локально могут быть так выбраны пространственно-временные координаты  (система отсчета), что интервал для малой области пространства-времени в этих координатах запишется так же, как он записывается для лоренцевских координат (систем отсчета) в плоском пространстве Минковского:

,

так что через точку пространства-времени проходит бесконечно много линий, имеющих нулевую «длину» (при определении длины в пространстве-времени через его «физическую метрику» — то есть, как интеграл от  ) — образующих световой конус, бесконечно много линий, длина которых вещественна (они все во внутренней области светового конуса), и бесконечно много тех, длина которых чисто мнима (вблизи данной точки они все во внешней области светового конуса с вершиной в ней, если они гладки).

55. Пространственно-временные графики и понятия «прошлое, настоящее и будущее». Пространственно-временные диаграммы

Любое обсуждение в космологии требует тщательного рассмотрения того, что мы можем видеть и когда мы можем это видеть. Хорошим способом отслеживать такие вещи являются пространственно-временные диаграммы. Пространственно-временная диаграмма является ничем иным, кроме графика, показывающего положение объекта, как функцию времени. Стандартное соглашение предусматривает, что время движется на диаграмме вверх, поэтому низ диаграммы является прошлым,или более ранним временем, а верх - будущим, или более поздним временем. Точка на таком графике описывает как положение (горизонтальная или x координата), так и время (вертикальная или t координата). "Точка" на пространственно-временной диаграмме называется событием.

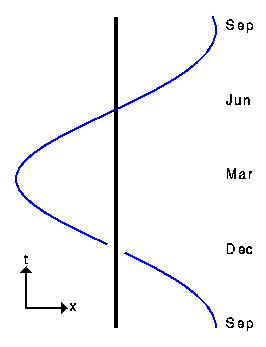
Приведенная выше картинка показывает пространственно-временную диаграмму Земли, движущейся вокруг Солнца. В этом рисунке перспектива используется, чтобы попытаться показать два пространственных измерения и ось времени на двумерном листе бумаги, но обычно мы будем просто показывать одну пространственную ось и не станем использовать перспективу.

Линия, представляющая расположение Земли, как функцию времени, называется мировой линией. Наклон мировой линии частицы показывает её скорость в системе координат диаграммы. 

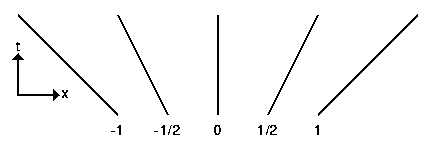
Приведенная выше пространственно-временная диаграмма показывает частицы с различными скоростями.

Из-за того, что в теории относительности скорость света является особой скоростью, пространственно-временные диаграммы часто изображают в единицах секунд и световых секунд, или лет и световых лет, таким образом, единичный наклон [угол в 45 градусов] соответствует скорости света. Набор всех мировых линий скорости света, проходящих через событие, определяет световые конусы данного события: световой конус прошлого и световой конус будущего. Пример световых конусов показан выше. Воображаемая сетовая картинка слева показывает световые конусы прошлого и будущего события, находящегося там, где пересекаются две мировые линии, в то время как схематичный рисунок справа легко использовать в более сложных диаграммах.