35. Электромагнитная индукция. Токи смещения.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в системе СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

   — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

Ток смещения или абсорбционный ток — понятие из области теории классической электродинамики. Введено Дж. К. Максвеллом при построении теории электромагнитного полядля описания слабых токов, возникающих при смещении заряженных частиц в диэлектриках.

Ток смещения в классической электродинамике

В природе существует три вида токов: ток проводимости, ток смещения и ток переноса. Во времена Максвелла, ток проводимости мог быть экспериментально зарегистрирован и измерен (например, амперметром, индикаторной лампой), тогда как движение зарядов внутри диэлектриков могло быть лишь косвенно оценено. Ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля.

При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения.

Ток смещения существует и в проводниках, по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:

Для различия ток проводимости и ток смещения принято обозначать разными символами — i и j соответственно.

В диэлектрике (например, в диэлектрике конденсатора) и в вакууме нет токов проводимости. Поэтому уравнение Максвелла пишется так —

36. Теория электромагнитного поля. Уравнение Максвелла.

Электромагни́тное по́ле — фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, представимое как совокупность электрического и магнитногополей, которые могут при определённых условиях порождать друг друга.

Электромагнитное поле (и его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это ещё одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.

В современной формулировке электромагнитное поле представлено тензором электромагнитного поля, компонентами которого являются три компоненты напряжённости электрического поля и три компоненты напряжённости магнитного поля (или — магнитной индукции)^[1], а также четырёхмерным электромагнитным потенциалом — в определённом отношении ещё более важным.

Действие электромагнитного поля на заряженные тела описывается в классическом приближении посредством силы Лоренца.

Квантовые свойства электромагнитного поля и его взаимодействия с заряженными частицами (а также квантовые поправки к классическому приближению) — предмет квантовой электродинамики, хотя часть квантовых свойств электромагнитного поля более или менее удовлетворительно описывается упрощённой квантовой теорией, исторически возникшей заметно раньше.

Возмущение электромагнитного поля, распространяющееся в пространстве, называется электромагнитной волной (электромагнитными волнами)^[2]. Любая электромагнитная волна распространяется в пустом пространстве (вакууме) с одинаковой скоростью — скоростью света (свет также является электромагнитной волной). В зависимости от длины волны электромагнитное излучение подразделяется на радиоизлучение, свет (в том числе инфракрасный и ультрафиолет), рентгеновское излучение и гамма-излучение.

Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающихэлектромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Четыре уравнения Максвелла обычно располагают попарно, но принцип разбиения на пары оказывается разным. Приведем принятую в основных литературных источниках запись уравнений Максвелла в дифференциальной форме, соответствующую системе единиц СГС:  rot В = μμ₀ j + (1/с²) ∂Е/∂t ,  ( 1 )       rot Е = – ∂B/∂t ,      ( 2 )  div Е = ρ/εε₀ ,                      ( 3 )       div B = 0 ,               ( 4 ) 

Закон Гаусса			Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля			Не существует магнитных зарядов.[~ 1]
Закон индукции Фарадея			Изменение магнитной индукции порождает вихревое электрическое поле.[~ 1]
Закон Ампера —Максвелла			Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

•  — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

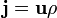•  — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²);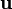

•  — скорость зарядов в данной точке;

•  — скорость света в вакууме (299 792 458 м/с);

•  — напряжённость электрического поля (в единицах СИ — В/м);

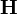•  — напряжённость магнитного поля (в единицах СИ — А/м);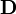

•  — электрическая индукция (в единицах СИ — Кл/м²);

•  — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с⁻²•А⁻¹);

•  — дифференциальный оператор набла, при этом:

 означает ротор вектора,

 означает дивергенцию вектора.