
- •1. Векторные и скалярные величины в физике. Сложение и умножение векторов.
- •Сложение векторов
- •2. Галилей – основоположник научного подхода к изучению природы.
- •Первый закон Ньютона
- •Второй закон Ньютона
- •Третий закон Ньютона
- •4. Система отсчета. Принцип относительности Галилея. Преобразование Галилея.
- •Вид преобразований при коллинеарных осях[4]
- •Формула преобразования скоростей
- •5. Гравитационное поле. Напряжённость гравитационного поля.
- •6. Масса инертная и гравитационная.
- •Определение
- •8. Векторы моментов силы и момента импульса.
- •9. Уравнение моментов. Закон сохранения момента импульса.
- •Оба эти условия не являются достаточными для покоя.
- •11. Иерархия научных законов. Законы сохранения в механике. Математическая формулировка законов сохранения. Закон Сохранения Импульса
- •Закон Сохранения Механической Энергии
- •12. История развития представлений о Вселенной. Законы Кеплера.
- •Средневековье Европа
- •Первый закон Кеплера (закон эллипсов)
- •Второй закон Кеплера (закон площадей)
- •Третий закон Кеплера (гармонический закон)
- •13. Взаимосвязь между свойствами Вселенной и возможностью появления в ней разумной жизни.
- •15. Понятие пространства. Измерение больших и малых расстояний.
- •16. Детерминизм Лапласа.
- •18. Распределение Максвелла.
- •19. Необратимые и обратимые процессы. Открытые, закрытые и изолированные системы.
- •20. Энтропия в изолированных и не изолированных системах.
- •21. Равновесие в системе, состоящей из большого числа частиц.
- •Для одноатомных газов
- •Для многоатомных газов
- •Для смесей газов
- •Для жидкостей
- •22. Второе начало термодинамики. Термодинамическое определение энтропии.
- •Термодинамическое определение энтропии
- •23. Статистическое определение энтропии, термодинамическая вероятность. Статистическое определение энтропии: принцип Больцмана
- •24. Стрела времени.
- •Ось времени в классической физике
- •Ось времени и теория относительности
- •25. Равновесные, слабо неравновесные и сильно неравновесные процессы.
- •26. Самоорганизация. Порядок через флуктуацию. Диссипативные системы.
- •27. Эффект Бернара как прототип явлений самоорганизации.
- •Основные характеристики
- •Принцип суперпозиции в электродинамике
- •30. Основные законы электростатики, закон Кулона, закон сохранения заряда.
- •Закон сохранения заряда в дифференциальной форме
- •31. Электрическое поле в диэлектриках и проводниках.
- •Основные уравнения и законы
- •Закон Фарадея
- •33. Магнитное поле в веществе. Магнитное поле в веществе
- •34. Движение частиц в электрическом и магнитном полях. Движение заряженных частиц
- •Однородном магнитном поле
- •Движение заряженных частиц
- •Неоднородном магнитном поле
- •Движение заряженных частиц
- •Однородном электрическом поле
- •Движение заряженных частиц
- •Неоднородном электрическом поле
- •35. Электромагнитная индукция. Токи смещения.
- •Закон Фарадея
- •Ток смещения в классической электродинамике
- •36. Теория электромагнитного поля. Уравнение Максвелла.
- •37. Электромагнитные волны.
- •38. Тепловое излучение. Квантовая гипотеза Планка.
- •Основные свойства теплового излучения
- •39. Фотоэффект.
- •Законы внешнего фотоэффекта
- •Внутренний фотоэффект
- •40. Принцип неопределённости.
- •Определение
- •41. Геометрическая оптика. Миражи.
- •Законы геометрической оптики
- •43. Когерентность. Способы получения когерентных пучков.
- •Виды когерентности
- •45. Применение явления интерференции.
- •Физические принципы
- •Источники света
- •Регистрирующие среды
- •47. Давление света.
- •48. Противоречия электродинамики и принципа относительности Галилея.
- •50. Основные постулаты специальной теории относительности.
- •Постулаты Специальной Теории Относительности (сто)
- •2 Рисунок 7.1.2.
- •51. Преобразования Лоренца.
- •Относительность промежутков времени
- •53. Сокращение длины и замедление времени.
- •55. Пространственно-временные графики и понятия «прошлое, настоящее и будущее». Пространственно-временные диаграммы
- •56. Экспериментальные подтверждения кривизны пространства и замедления времени.
- •57. Эквивалентность массы и энергии.
- •Масса покоя как вид энергии
- •Понятие релятивистской массы
- •58. Строение атома. Опыты Резерфорда.
- •Квантовые числа электронов
- •60. Корпускулярно-волновой дуализм.
- •Корпускулярно-волновая двойственность света
- •61. Роль прибора при исследовании микрообъектов.
- •62. Уравнение Шредингера.
- •Общий случай
- •63. Частица в потенциальном «ящике».
- •64. Квантовые числа и периодическая система элементов.
- •65. Радиоактивность. Период полураспада.
- •Виды лучей радиоактивного распада
- •Альфа-распад
- •Бета-распад
- •Гамма-распад (изомерный переход)
- •66. Альфа, бета и гамма распад.
- •67. Открытие нейтрона. Основные свойства нейтронов и протонов:масса, спин и магнитный момент.
- •69. Ядерные силы.
- •70. Ядерные реакции. Типы и классификация.
- •Термоядерный синтез
- •Фотоядерная реакция
- •71. Ядерные реакции под действием нейтронов.
- •По величине спина
- •По видам взаимодействий
- •Составные частицы
- •Фундаментальные (бесструктурные) частицы
- •75. Классификация элементарных частиц.
- •77. Лептоны. Закон сохранения лептонного числа.
- •Свойства
- •Лептонное число
1. Векторные и скалярные величины в физике. Сложение и умножение векторов.
Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление. скорость(v),сила(F),перемещение(s),импульс(р),энергия(Е)
Скалярными называют величины, имеющие численное значение, но не имеющие направления. масса(m),объем(V),площадь(S),время(t),высота(h)
Сложение векторов
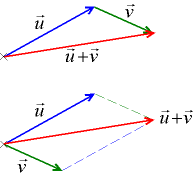
Два вектора u, v и вектор их суммы
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Правило треугольника.
Для сложения двух векторов ![]() и
и ![]() по
правилу треугольника оба
эти вектора переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
по
правилу треугольника оба
эти вектора переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограммаоба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
А модуль (длину)
вектора суммы ![]() определяют
по теореме
косинусов
определяют
по теореме
косинусов ![]() где
где ![]() —
угол между векторами, когда начало
одного совпадает с концом другого. Так
же используется формула
—
угол между векторами, когда начало
одного совпадает с концом другого. Так
же используется формула ![]() теперь
—
угол между векторами выходящими из
одной точки.
теперь
—
угол между векторами выходящими из
одной точки.
Скалярным
произведением векторов ![]() и
и ![]() называют
число, равное
называют
число, равное ![]() ,
где
,
где ![]() — угол между
векторами
— угол между
векторами ![]() и
и ![]() .
Обозначения:
.
Обозначения: ![]() или
или ![]() .
.
Если один из векторов является нулевым, то несмотря на то, что угол не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
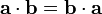 — коммутативность.
— коммутативность. — дистрибутивность.
— дистрибутивность.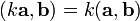 —
линейность по
отношению к умножению на число.
—
линейность по
отношению к умножению на число. — норма
вектора (Квадрат
вектора).
— норма
вектора (Квадрат
вектора).
2. Галилей – основоположник научного подхода к изучению природы.
итальянский физик, механик, астроном, философ и математик, оказавший значительное влияние на науку своего времени.
Он первым использовал телескоп для наблюдения небесных тел[1] и сделал ряд выдающихся астрономических открытий. Галилей — основатель экспериментальной физики.
При жизни был известен как активный сторонник гелиоцентрической системы мира, что привело Галилея к серьёзному конфликту с католической церковью.
Галилей по праву считается основателем не только экспериментальной, но — в значительной мере — и теоретической физики. В своём научном методе он осознанно сочетал продуманный эксперимент с его рациональным осмыслением и обобщением, и лично дал впечатляющие примеры таких исследований. Иногда из-за недостатка научных данных Галилей ошибался (например, в вопросах о форме планетных орбит, природе комет или причинах приливов), но в подавляющем большинстве случаев его метод приводил к цели. Характерно, что Кеплер, располагавший более полными и точными данными, чем Галилей, сделал правильные выводы в тех случаях, когда Галилей ошибался.
сама идея экспериментального метода познания, который должен дополнять и подтверждать дедуктивно-умозрительные построения, была чужда аристократическому духу античной физики. В Европе ещё в XIII веке Роберт Гроссетест и Роджер Бэкон призвали к созданию экспериментальной науки, которая на математическом языке сможет описать природные явления, однако до Галилея в реализации этой идеи не было существенного продвижения: научные методы мало отличались от теологических, и ответы на научные вопросы по-прежнему искали в книгах древних авторитетов. Научная революция в физике начинается с Галилея.
В отношении философии природы Галилей был убеждённым рационалистом. Он считал, что законы природы постижимы для человеческого разума.
Галилей считается одним из основателей механицизма. Этот научный подход рассматривает Вселенную как гигантский механизм, а сложные природные процессы — как комбинации простейших причин, главная из которых — механическое движение.
Опыт Галилей рассматривал не как простое наблюдение, а как осмысленный и продуманный вопрос, заданный природе. Он допускал и мысленные эксперименты, если их результаты не вызывают сомнений. При этом он ясно представлял, что сам по себе опыт не даёт достоверного знания, и полученный от природы ответ должен подвергнуться анализу, результат которого может привести к переделке исходной модели или даже к замене её на другую. 3. Законы Ньютона.
