Лабораторна робота №1

1. Визначення випадкових сигналів, їх класифікація.

С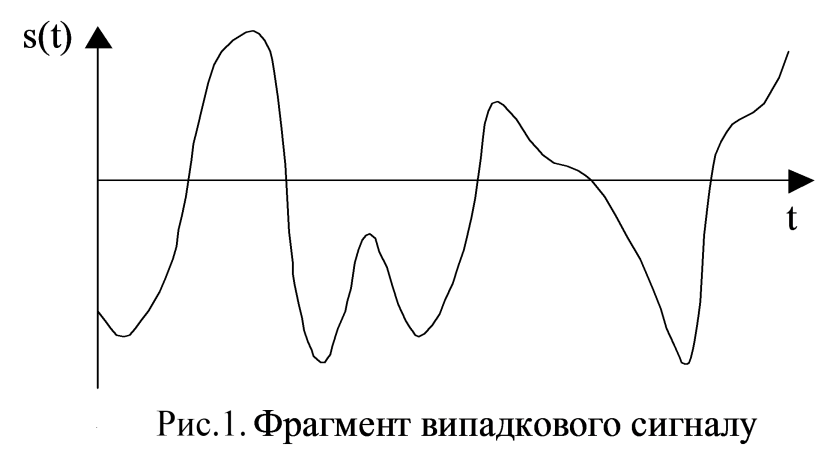 игнал вважається випадковим, якщо його майбутні значення не можна визначити наперед, тобто ці значення непередбачувані або можуть бути визначені з якою-небудь вірогідністю (рис. 1). Кожне значення сигналу прийняте на приймальному пункті, є для адресата випадковим, оскільки адресат наперед не знає змісту інформації, яку несе даний сигнал. Випадковими сигналами також є завади, які перешкоджають надійному прийманню інформаційних сигналів.

Випадковий сигнал представляє собою сукупність миттєвих значень розподілених в часі.

Випадкові сигнали поділяються на:

• Стаціонарні – такі сигнали, імовірнісні характеристики яких не залежать від часу. Стаціонарний сигнал (процес) може бути ергодичним (імовірнісні характеристики якого не залежать від номера реалізації і від часу) або неергодичним (імовірнісні характеристики від поточного часу та від номера реалізації не співпадають).

• Нестаціонарні - такі сигнали, імовірнісні характеристики яких залежать від часу.

2. Основні характеристики випадкових сигналів

Основними характеристиками випадкових сигналів є:

• миттєве значення - це значення сигналу в довільний момент часу.

• максимальне та мінімальне значення сигналу. Максимальне значення – найбільше відхилення від середнього в додатню сторону. Мінімальне значення – найбільше відхилення від середнього у від’ємну сторону.

• Густина розподілу ймовірності появи миттєвих значень випадкового сигналу P(U) - дозволяє визначити ймовірність появи сигналу на певних рівнях в деякому інтервалі.

Основними законами розподілу ймовірності миттєвих значень є нормальний (рис.2а) та рівномірний (рис.2б).

• Нормальний закон розподілу

Крива для нормального закону розподілу густини ймовірності миттєвих значень має вигляд, як показано на рис.2а та представляється функцією Гаусса:

де σ² - дисперсія;

- математичне очікування;

U - значення сигналу, яке змінюється в діапазоні існування сигналу.

Рис.2а. Нормальний закон розподілу

На рис. 2а представлений закон розподілу густини ймовірності миттєвих значень із математичним очікуванням =0. В реальних процесах із нормальним законом розподілу може бути .

Для процесів із нормальним законом розподілу густини ймовірності миттєвих значень, імовірність попадання в інтервал, який обмежений значенням похибки (квантилем), що відповідає значенню від середнього значення дорівнює:

• Рівномірний закон розподілу

На рис.2б зображено криву густини ймовірності миттєвих значень для рівномірного закону розподілу.

Рис.2б. Рівномірний закон розподілу

Неперервна випадкова величина U має рівномірний закон розподілу, на відрізку [a, b], якщо її густина ймовірності P (U) постійна на цьому відрізку і дорівнює нулю поза ним, тобто

_{В цьому випадку математичне очікування} =(а+в)/2, тобто =0, а дисперсія

• Ф ункція ймовірності випадкового сигналу (процесу) F(U), яка показує ймовірність появи випадкової величини на інтервалі від до U. Густина розподілу ймовірності зв’язана з функцією розподілу таким чином:

Нагадаємо властивості функції розподілу F(U) (рисунок 2):

1. функція розподілу завжди є більшою за 0 і ніколи не перевищує 1;

2) функція розподілу завжди є монотонно зростаючою.

• Середнє значення сигналу або – характеризує постійну складову випадкового сигналу або зміщення (offset) сигналу по осі У (вертикаль).

У таблиці 1 наведені формули розрахунку параметрів випадкового сигналу.

• Дисперсія або – характеризує середню потужність змінної складової випадкового сигналу (табл.1)

• Середнє квадратичне значення

або

Наприклад, для неперервного сигналу

Фізичний сенс це деяка постійна напруга, яка має потужність таку ж саму як і випадковий процес, використовується для порівняння випадкових сигналів за потужністю (енергією).

Таблиця 1

Формули розрахунку параметрів випадкового сигналу

№	Параметр	Дискретний сигнал (сигнал, що представляється у вигляді окремих значень, що взяті за часом)	Неперервний сигнал (може приймати будь-які рівні значень в будь-якому інтервалі часу )
1.	Середнє значення	, де N- об’єм реалізації	або , де Т – довжина реалізації в секундах
2.	Дисперсія	, де - центрована випадкова величина процесу (сигналу), тобто змінна складової сигналу – без постійної складової	- по часу t - по P(U)

• Гістограма є графічним поданням розподілу частот за інтервалами. Гістограма будується як множина прямокутників, основою яких є довжина інтервалу, а висота — пропорційна до відповідної частоти (рис.4).

Рис. 4

При нескінченно великій кількості інтервалів частота W_i є наближенням імовірності потрапляння випадкової величини в i-й інтервал:

де Р(х) – щільність імовірності випадкової величини.

Цю властивість використовують для порівняння теоретичного й емпіричного розподілів. Один із таких способів полягає в графічному зіставленні передбачуваного теоретичного розподілу з емпіричним, тобто графік щільності ймовірностей р(х) (криву розподілу) зіставляють із гістограмою. Якщо передбачуваний теоретичний розподіл добре узгоджується з дослідним, то при досить великому n і вдалому виборі інтервалів гістограма буде близька до кривої розподілу.

Гістограма будується наступним чином.

Вхідний сигнал характеризується U_max та U_min. Різниця цих значень є діапазон D = U_max - U_min, що включає всі значення сигналу. При побудові гістограм весь діапазон миттєвих значень сигналу поділяється на n інтервалів. Число інтервалів можемо приблизно оцінити з виразу: . Кожний інтервал j є (1; m)має свої межі від U_jmin до U_jmax, при U_jmin ≤ U_i ≤ U_jmax. Підрахувавши число n_j попадань, в кожному з наведених інтервалів, можемо визначити частотупопадань W_j = n_j / N та побудувати графык (рис. 4). Величина W_j представляє собою ймовірність знаходження миттєвих значень (випадкової величини)сигналу у j інтервал.