
- •Министерство образования и науки российской федерации
- •Физические теории пластичности
- •Оглавление
- •Основные обозначения
- •Сокращения
- •Введение
- •Подход к построению определяющих соотношений с использованием внутренних переменных
- •Структура конститутивной модели с внутренними переменными
- •О многоуровневых моделях
- •Вопросы к «Введению»
- •Глава 1. Основные понятия и определения
- •1.1. О геометрической нелинейности и независимых от выбора системы отсчета тензорзначных характеристиках
- •1.2. Классический и обобщенные континуумы
- •Вопросы к главе 1
- •Глава 2. Механизмы неупругого деформирования
- •2.1. О дислокационных механизмах неупругого деформирования
- •2.2 Взаимодействия дислокаций с дислокациями и точечными дефектами
- •2.3 Деформирование монокристалла двойникованием
- •2.4. Закон Шмида
- •2.5. Механизмы и модели деформационного упрочнения
- •Вопросы к главе 2
- •Глава 3. Кинематика неупругого деформирования
- •3.1. Уравнение Орована
- •3.2. Моды неупругого деформирования монокристаллов
- •3.3. Статистически накопленные и геометрически необходимые дислокации, изгибы–кручения решетки
- •3.4 Ротационные моды деформирования, модели ротации
- •Вопросы к главе 3
- •Глава 4. Жесткопластические модели
- •4.1. Модель Закса
- •4.2. Модель Тейлора
- •4.3. Модель Бишопа-Хилла
- •Вопросы к главе 4
- •Глава 5. Упругопластические модели
- •5.1. Модель Линя
- •5.2. Направления развития упругопластических моделей
- •Вопросы к главе 5
- •Глава 6. Вязкоупругие и вязкопластические модели
- •Вопросы к главе 6
- •Глава 7. Упруговязкопластические модели
- •7.1 Анализ упруговязкопластических моделей [64, 114]
- •7.2. Краткий обзор работ по упруговязкопластическим моделям
- •Вопросы к главе 7
- •Глава 8. Структура и алгоритмы реализации многоуровневых моделей
- •8.1. Наиболее распространенная схема построения многоуровневых моделей, их структура и классификация
- •8.2. Согласование определяющих соотношений масштабных уровней и конкретизация независящей от выбора системы отсчета производной
- •8.3. Классификация внутренних переменных и уравнений конститутивной модели на примере двухуровневой упруговязкопластической модели
- •8.4. Модель поворотов кристаллической решетки, учитывающая взаимодействие элементов мезоуровня
- •8.5. Алгоритм реализации двухуровневой упруговязкопластической модели
- •Библиографический список
- •Предметный указатель
8.5. Алгоритм реализации двухуровневой упруговязкопластической модели
Рассмотрим алгоритм численной реализации
двухуровневой модели, представленной
в п.8.3; для определенности в качестве
связей используются соотношения -,
рассматривается кинематическое
нагружение представительного объема,
т.е.
![]() задан (при моделировании процесса
одноосного или двухосного нагружения
в процедуру добавляется корректировка
для обеспечения соответствующего
напряженного состояния[48]).
задан (при моделировании процесса
одноосного или двухосного нагружения
в процедуру добавляется корректировка
для обеспечения соответствующего
напряженного состояния[48]).
Математически задача сводится к интегрированию системы обыкновенных дифференциальных уравнений. Для интегрирования выбрана неявная схема Адамса–Моултона второго порядка. Известно, что неявные схемы обладают большей устойчивостью по сравнению с явными схемами; при этом схема Адамса–Моултона хорошо подходит для решения обыкновенных дифференциальных уравнений с сильно нелинейными правыми частями, что имеет место в рассматриваемом случае.
Разностный аналог метода Адамса–Моултона
второго порядка для дифференциального
уравнения
![]() на шаге
на шаге
![]() реализуется согласно следующему
уравнению [5]:
реализуется согласно следующему
уравнению [5]:
![]() .
.
Поскольку для рассматриваемой системы
уравнений аналитическое решение системы
типа , как правило, не существует, то
![]() предлагается находить с помощью
итерационного процесса вида:
предлагается находить с помощью
итерационного процесса вида:
![]()
Завершение итерационного процесса
производится при выполнении условия
![]() – заданное малое число. Сходимость
процесса наблюдается при малых шагах
интегрирования
– заданное малое число. Сходимость
процесса наблюдается при малых шагах
интегрирования
![]() ,
К – константа в условии Липшица
для правой части исходного дифференциального
уравнения.
,
К – константа в условии Липшица
для правой части исходного дифференциального
уравнения.
В качестве начального приближения
выбирается
![]() .
Тогда на первой итерации получаем
решение
.
Тогда на первой итерации получаем
решение
![]() ,
,
соответствующее использованию явной схемы Эйлера, имеющей первый порядок аппроксимации. Далее,
![]()
что для рассматриваемого одномерного случая соответствует схеме Рунге-Кутта второго порядка
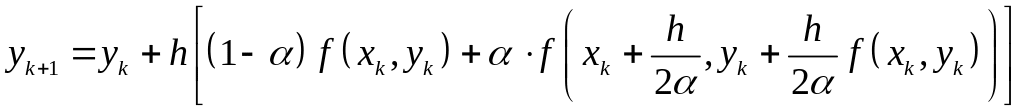
с коэффициентом
![]() .
.
На третьей итерации можно ожидать
повышения порядка аппроксимации до
третьего, и так далее. Однако необходимо
иметь в виду, что сама исходная схема
Адамса-Моултона имеет второй порядок,
а значит целесообразно ограничивать
общее число итераций двумя (так как
точность выше второго порядка никак не
достижима только за счет более точного
определения
как решения ). Алгоритм реализации
схемы Адамса-Моултона для системы
уравнений аналогичен приведенному выше
с заменой скалярных переменных на
векторные (![]() ).
).
Согласно вышеприведенному подходу
итерационного определения значений
неизвестных на конец шага, из схемы
Адамса–Моултона второго порядка
получается следующие соотношения для
определения вектора неизвестных на
конец шага
![]() :
:
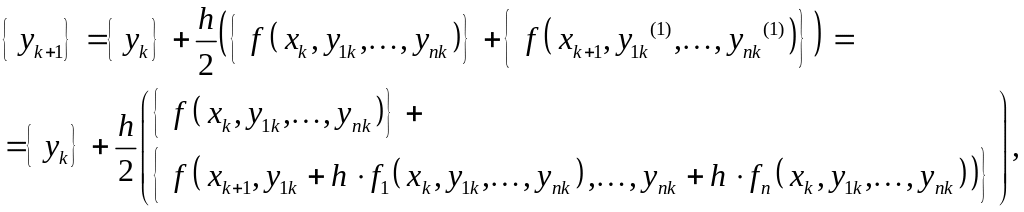
где использованы обозначения:
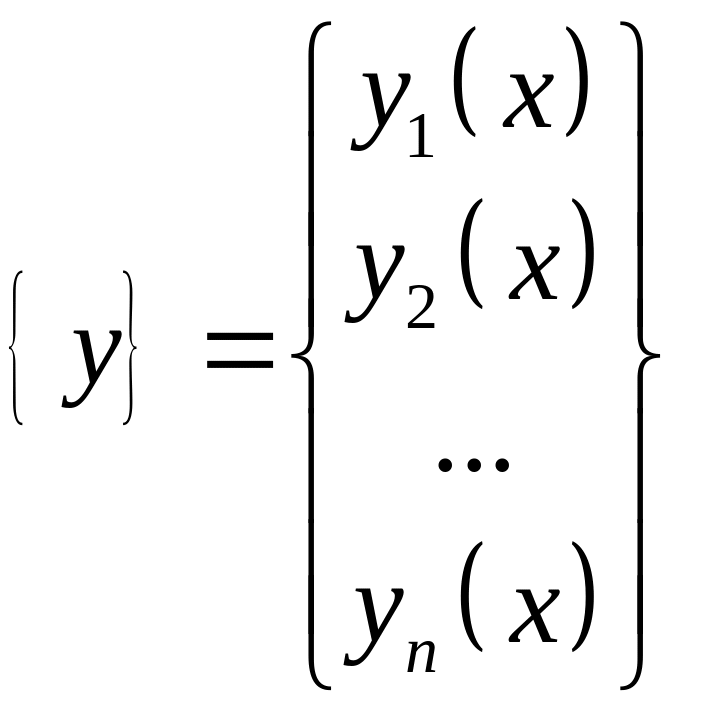 –
вектор неизвестных,
–
вектор неизвестных,
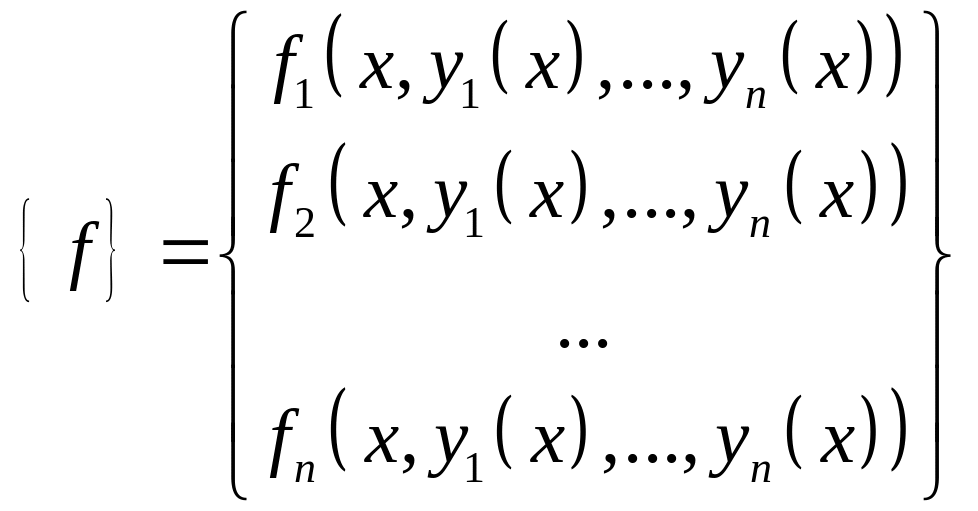 –
вектор правой части.
–
вектор правой части.
Схему также называют схемой
«предиктор-корректор»: в соответствии
с ней на первой итерации каждого шага
по времени скоростные соотношения
интегрируются по явной схеме Эйлера
(вычисляются
![]() ),
на второй итерации, по сути, происходит
уточнение найденных по схеме Эйлера
неизвестных.
),
на второй итерации, по сути, происходит
уточнение найденных по схеме Эйлера
неизвестных.
Рассмотрим процедуру интегрирования
уравнений модели на некотором временном
шаге
![]() .
На начало шага
.
На начало шага
![]() известны значения параметров отклика
и всех внутренних переменных: напряжения
макроуровня
известны значения параметров отклика
и всех внутренних переменных: напряжения
макроуровня
![]() ;
для каждого кристаллита:
;
для каждого кристаллита:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ;
также задано нагружение
;
также задано нагружение
![]() ,
для простоты рассмотрения алгоритма
примем нагружение постоянным на шаге
,
для простоты рассмотрения алгоритма
примем нагружение постоянным на шаге
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Необходимо в результате интегрирования
уравнений двухуровневой модели на шаге
определить значения вышеперечисленных
переменных на конец временного шага
.
Необходимо в результате интегрирования
уравнений двухуровневой модели на шаге
определить значения вышеперечисленных
переменных на конец временного шага
![]() .
.
I. На первой итерации выполняется интегрирование системы уравнений с помощью явной схемы Эйлера.
Вычисления на мезоуровне
1. В цикле по кристаллитам осуществляются вычисления скоростей сдвигов, скоростей критических напряжений, определяются сдвиги и критические напряжения на конец шага для первой итерации (индекс кристаллита опущен).
1а. Определяются скорости сдвигов и сдвиги на конец шага:
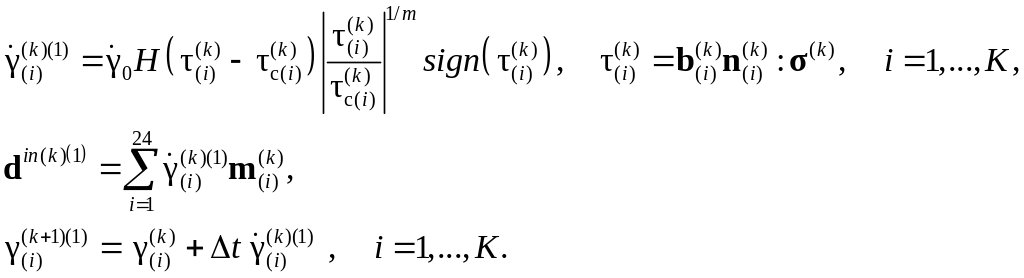
1b. Находятся скорости критических напряжений и критические напряжения на конец шага:
![]()
![]()
2. В цикле по кристаллитам осуществляются вычисления скоростей и значений на конец шага остальных переменных мезоуровня для первой итерации (индекс кристаллита опущен). Разделение на два цикла выполнено для реализации предлагаемой модели поворота, где спин решетки кристаллита зависит как от скоростей неупругих сдвигов в нем, так и в от скоростей неупругих сдвигов в соседних зернах.
2а. Определяется скорость моментных напряжений относительно КСК:
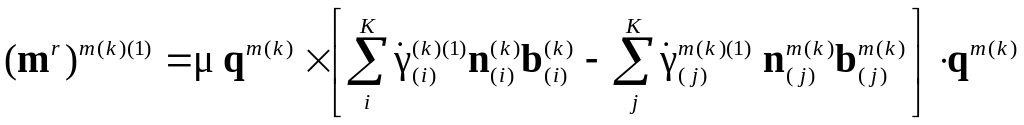 ,
,
![]()
![]() ,
,
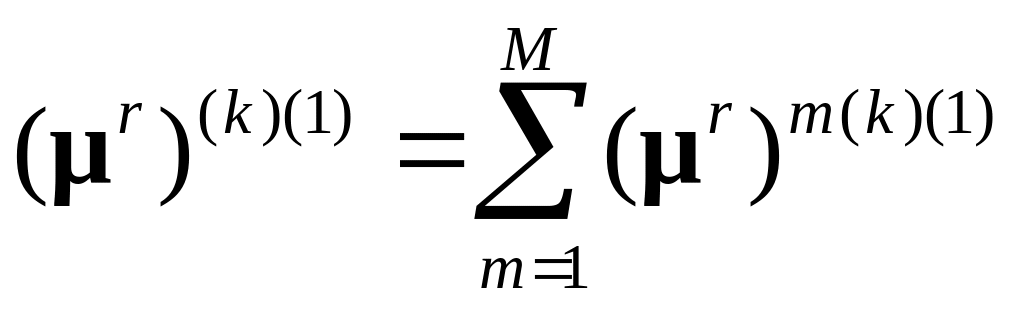 .
.
2b. Находится «решеточная» составляющая поворота :
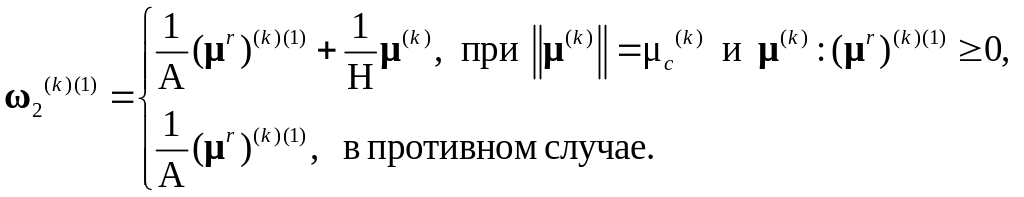
2с. Определяется «материальная» составляющая поворота и полный спин решетки:
![]()
![]() .
.
2d. Находится скорость моментных напряжений относительно ЛСК:
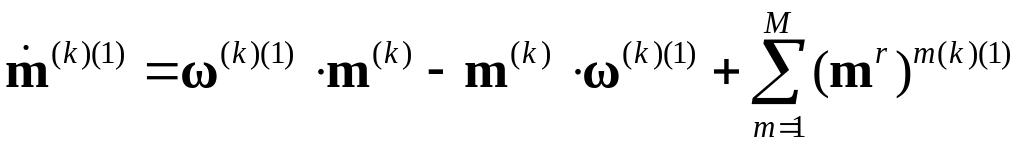 ,
,
![]() .
.
2e. Определяются моментные напряжения на конец шага:
![]() .
.
2f. Находятся скорости изменения нормалей и их ориентация на конец шага:
![]() ,
,
,
,
![]() ,
.
,
.
2g. По тензору спина определяется соответствующий вектор скорости поворота:
![]() .
.
2h. Находится ориентационный тензор (совмещающий кристаллографическую и лабораторную системы координат) после первой итерации путем последовательного определения
оси поворота
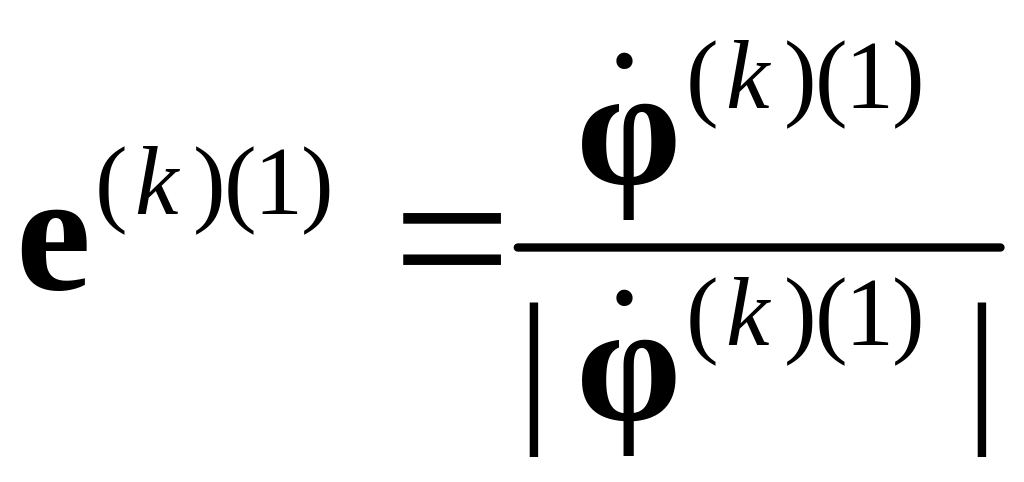 ,
,
угла поворота
![]() ,
,
тензора поворота за шаг
![]() ,
,
ориентационного тензора
![]() .
.
Примечание. Тензор
![]() связывает компоненты произвольного
вектора в кристаллографической
связывает компоненты произвольного
вектора в кристаллографической
![]() ,
и лабораторной системе координат
,
и лабораторной системе координат
![]() :
:
![]() ,
,
![]() ,
,
где
![]() – компоненты
в лабораторной системе координат.
– компоненты
в лабораторной системе координат.
Аналогичные преобразования для компонент
произвольного тензора второго ранга Т
на
![]() принимают вид:
принимают вид:
![]() ,
,
![]() ,
,
для тензора четвертого ранга –
![]() ,
,
![]() .
.
2i. Определяются значения
![]() (по
(по
![]() и известным компонентам в кристаллографической
системе координат с использованием
вышеприведенных соотношений).
и известным компонентам в кристаллографической
системе координат с использованием
вышеприведенных соотношений).
2j. Находятся скорости напряжений и напряжения:
![]() ,
, ![]() .
.
Вычисления на макроуровне
3a. Определяются значения внутренних переменных макроуровня:
тензор спина
![]() ,
,
тензор эффективных упругих свойств, его флуктуаций, флуктуаций деформации скорости, спина и напряжений:
![]() ,
,
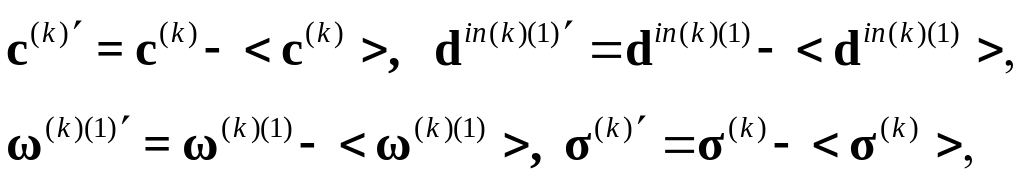
неупругая составляющая тензора деформации скорости
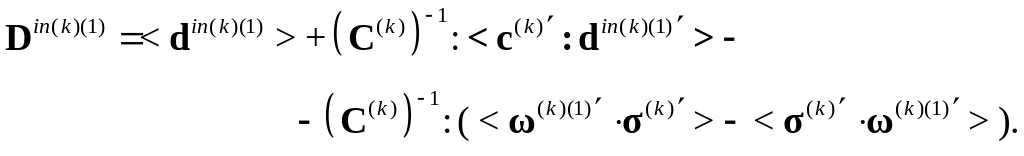
3b. Находятся скорости напряжений и напряжения после первой итерации.
![]()
![]()
II. Выполняется вторая итерация схемы Адамса–Моултона, находятся значения переменных на конец шага.
Вычисления на мезоуровне
1. В цикле по кристаллитам осуществляются вычисления скоростей сдвигов, скоростей критических напряжений, определяются сдвиги и критические напряжения на конец шага для второй итерации (индекс кристаллита опущен).
1а. Определяются скорости сдвигов, скорость деформации и сдвиги на конец шага:
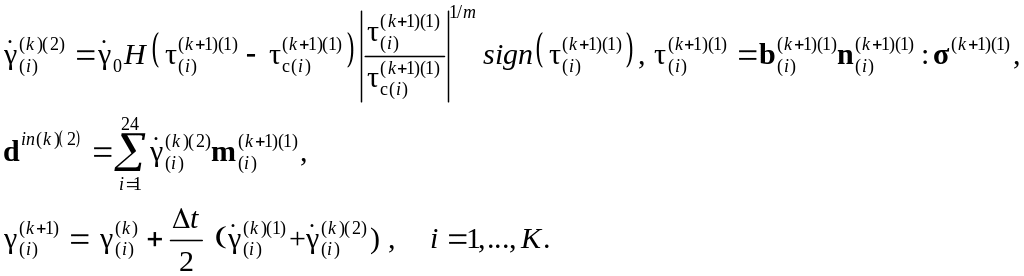
1b. Находятся скорости критических напряжений и критические напряжения на конец шага:
![]()
![]()
2. В цикле по кристаллитам осуществляются вычисления скоростей и значений на конец шага остальных переменных мезоуровня для первой итерации (индекс кристаллита опущен).
2а. Определяется скорость моментных напряжений относительно КСК:
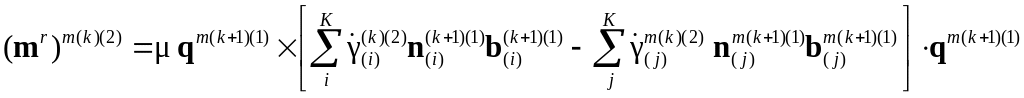
![]() ,
,
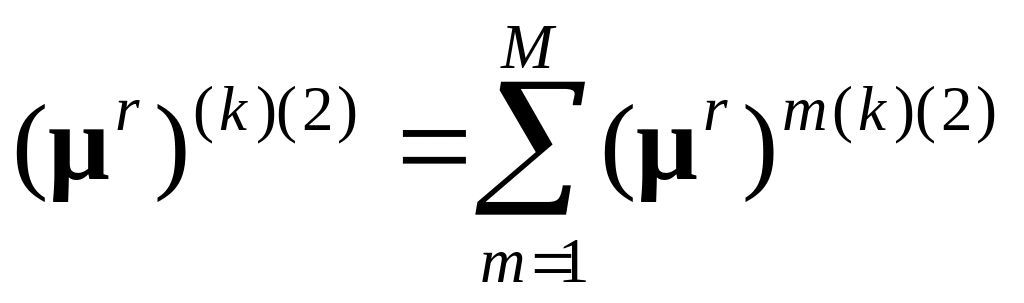 .
.
2b. Находится «решеточная» составляющая поворота :

2с. Определяется «материальная» составляющая поворота и полный спин решетки:
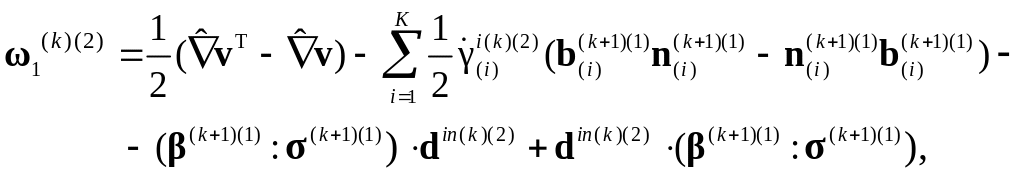
![]() .
.
2d. Находится скорость моментных напряжений относительно ЛСК:
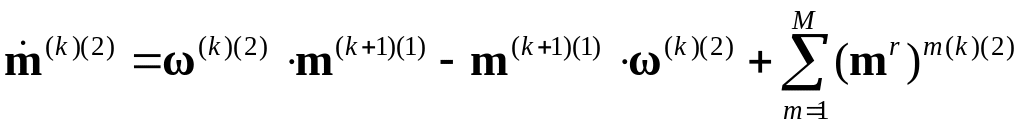 ,
,
![]() .
.
2e. Определяются моментные напряжения на конец шага:
![]() .
.
2f. Находятся скорости изменения нормалей и их ориентация на конец шага:
![]() ,
,
,
,
![]() ,
,
,
,
при необходимости вектор нормали
![]() нормируется.
нормируется.
2g. По тензору спина определяется соответствующий вектор скорости поворота:
![]() .
.
2h. Находится ориентационный тензор (совмещающий кристаллографическую и лабораторную системы координат) после второй итерации путем последовательного определения
«среднего» вектора скорости поворота
![]() ,
,
оси поворота
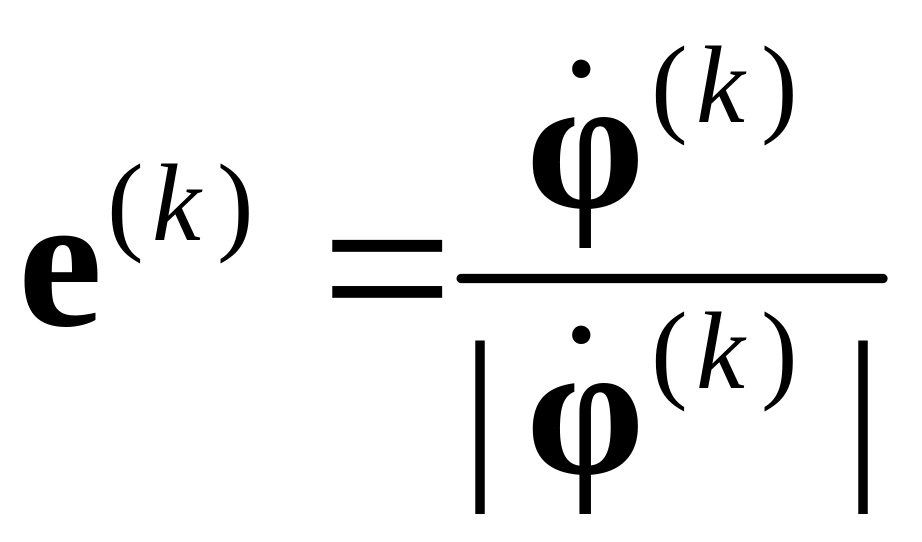 ,
,
угла поворота
![]()
тензора поворота за шаг
![]() ,
,
ориентационного тензора.
![]() .
.
2i. Определяются значения
![]() (по
(по
![]() и известным компонентам в КСК).
и известным компонентам в КСК).
2j. Находятся скорости напряжений и напряжения:
![]() ,
, ![]() .
.
Вычисления на макроуровне
3a. Определяются значения внутренних переменных макроуровня:
тензор спина
![]()
тензор эффективных упругих свойств, его флуктуаций, флуктуаций деформации скорости, спина и напряжений:
![]()
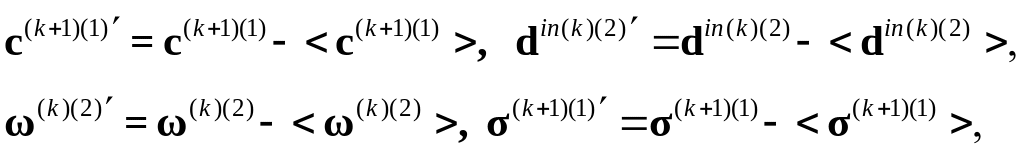
неупругая составляющая тензора деформации скорости
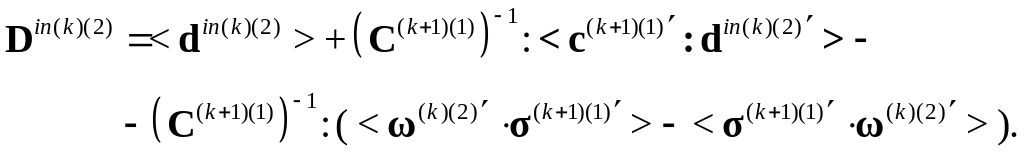
3b. Находятся скорости напряжений и напряжения после второй итерации.
![]()
![]() .
.
Таким образом, в результате вышеприведенных операций будут определены значения всех необходимых переменных на конец шага.
Отметим, что затраты машинного времени можно снизить при использовании параллельных вычислений: разбивать всю выборку кристаллитов, соответствующую представительному объему макроуровня, на несколько частей, расчеты на текущем шаге для которых проводить на отдельных вычислительных узлах.
Вопросы к главе 8
1. Назовите основные классификационные признаки многоуровневых моделей.
2. Какие гипотезы применяются в многоуровневых моделях для связи переменных различных уровней? Проведите их анализ.
3. Опишите элементы мезоуровня, используемые в многоуровневых моделях, приведите их основные харктеристики.
4. Какое физическое уравнение обычно используется в качестве определяющего соотношения на макро- и мезоуровне?
5. Приведите схему построения двухуровневой модели, перечислите ее достоинства и недостатки.
6. Опишите процедуру согласования определяющих соотношений двухуровневой модели.
7. Приведите основные понятия, используемые при построении модели ротации решетки. В чем состоит отличие предлагаемой модели «решеточного поворота» от известных моделей ротации (Тейлора, «материального поворота»)?
8. Запишите соотношение для определения вектора моментных напряжений, проведите его физический анализ для случая одиночного скольжения дислокаций при различной ориентации СС и границ кристаллита.
9. Приведите и проанализируйте соотношение для скорости «решеточного поворота».
10. Приведите алгоритм реализации метода Адамса–Моултона для ОДУ с векторными переменными.
11. Опишите алгоритм реализации двухуровневой упруговязкопластической модели.
12. Предложите модификацию вышеуказанного алгоритма для исследования неизотермических процессов деформирования.
Задачи и упражнения
Определить законы преобразования при замене системы отсчета локальных основных и взаимных материальных базисов в отсчётной и текущих конфигурациях.
Определить законы преобразования при замене системы отсчета правых и левых мер деформации.
Определить законы преобразования при замене системы отсчета мер напряжений, энергически сопряженных мерам деформации из предыдущей задачи.
Найти законы преобразования при замене системы отсчета бесконечно малого материально отрезка в текущей конфигурации и относительной скорости его конца, после чего установить законы преобразования тензоров градиента скорости перемещений, деформации скорости и вихря.
Убедится в невыполнении принципа материальной индифферентности для закона Гука
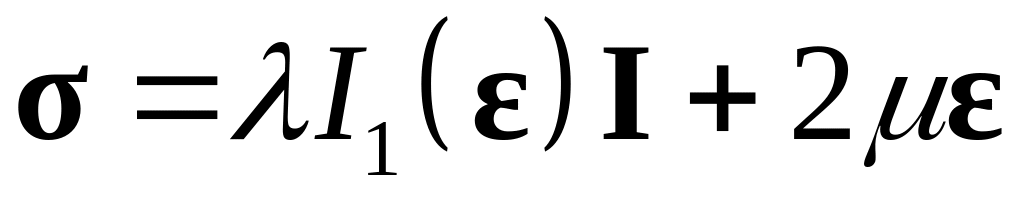 .
В каких условиях допустимо использование
данного закона?
.
В каких условиях допустимо использование
данного закона?Определить типы объективности следующих тензоров, характеризующих деформации: градиентов места, градиентов перемещений, мер деформаций Коши-Грина, Альманси, обратной Коши-Грина, Фингера, левой и правой мер искажения, левой и правой мер Генки, тензоров деформаций, ортогонального тензора, сопровождающего деформацию.
Определить типы объективности различных объективных производных тензоров, характеризующих деформации (упр. 6), тензора деформации скорости и тензора вихря.
Определить типы объективности следующих тензоров, характеризующих напряжения: тензора напряжений Коши, первого и второго тензоров напряжений Пиола-Кирхгоффа, взвешенного тензора Кирхгоффа, тензора напряжений Био, энергетического тензора напряжений (верхней конвективной формы тензора напряжений)
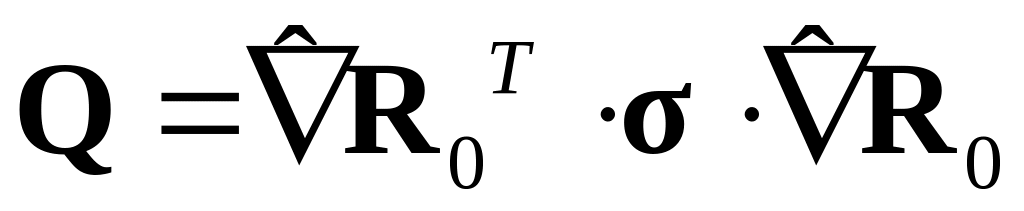 ,
нижней
,
нижней
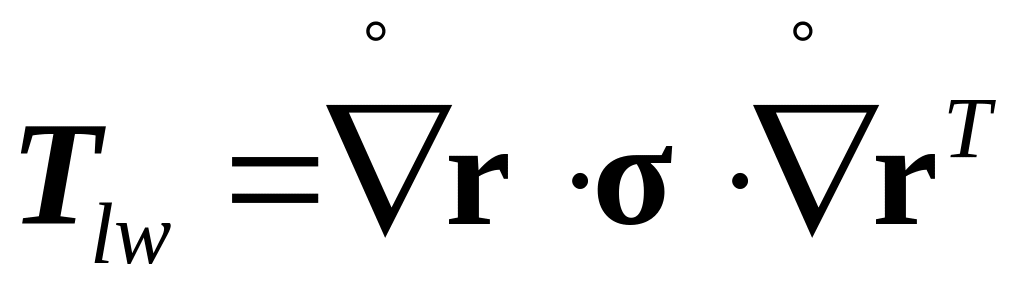 ,
правой
,
правой
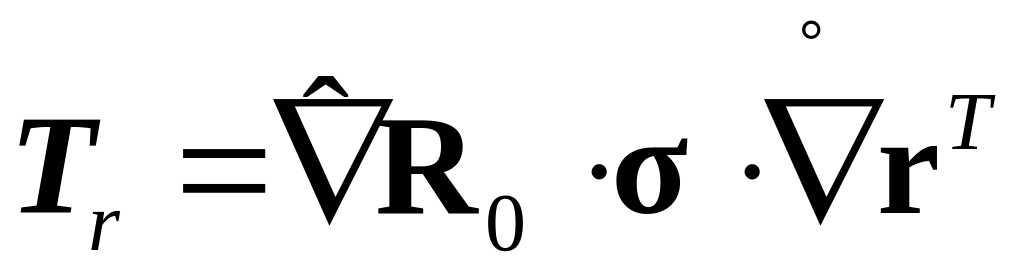 и левой
и левой
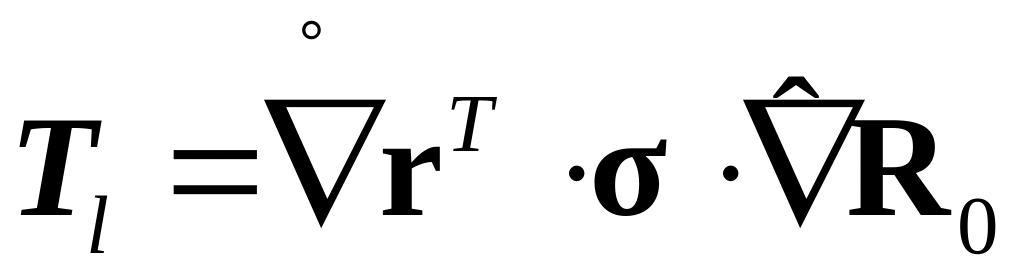 конвективных форм тензора напряжений,
ротационной формы тензора напряжений
конвективных форм тензора напряжений,
ротационной формы тензора напряжений
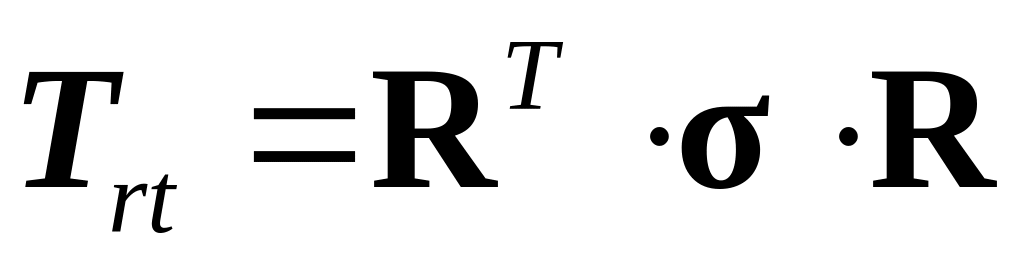 .
.Показать справедливость соотношения .
Показать, что тензор
 является девиатором и несимметричным
тензором.
является девиатором и несимметричным
тензором.Используя потенциал для классической гиперупругой среды получить ОС .
В точке M в декартовой системе координат компоненты тензора моментных напряжений имеют вид:
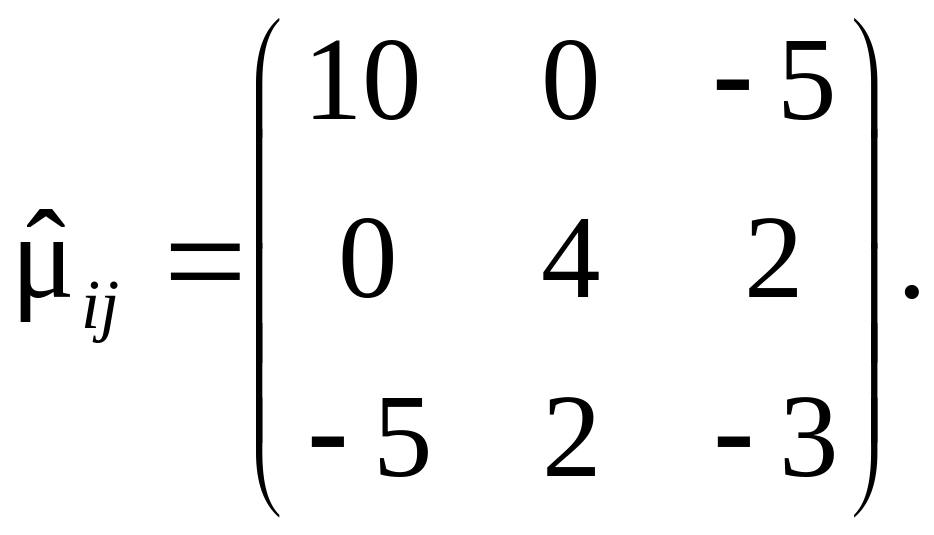
Определить вектор моментных напряжений
![]() на площадке с нормалью
на площадке с нормалью
![]() .
.
Поверхностью тензора напряжений σ для некоторой точки M сплошной среды называется такое геометрическое место точек, декартовы координаты xi которых удовлетворяют условию σijxixj=const, где σij – компоненты тензора σ в точке M. Определить форму поверхности напряжений для точки среды, где компоненты тензора напряжений в ортогональной декартовой системе координат имеют следующие значения:
а) σ11=σ22=σ33=σ, σij=0 при i≠j – всестороннее растяжение (сжатие);
б) σ11=σ, остальные σij=0 – одноосное растяжение (сжатие);
в) σ12=σ21=τ, остальные σij=0 – простой сдвиг;
г) σ11=A, σ22=B, σ33=C, σij=0 при i≠j – напряженное состояние общего вида в главных осях тензора напряжений. Исследовать вид поверхности напряжений в зависимости от знаков A, B, C. [25]
В кубическом кристалле происходит сдвиг скольжением на величину α по плоскости (0 1 1) в направлении
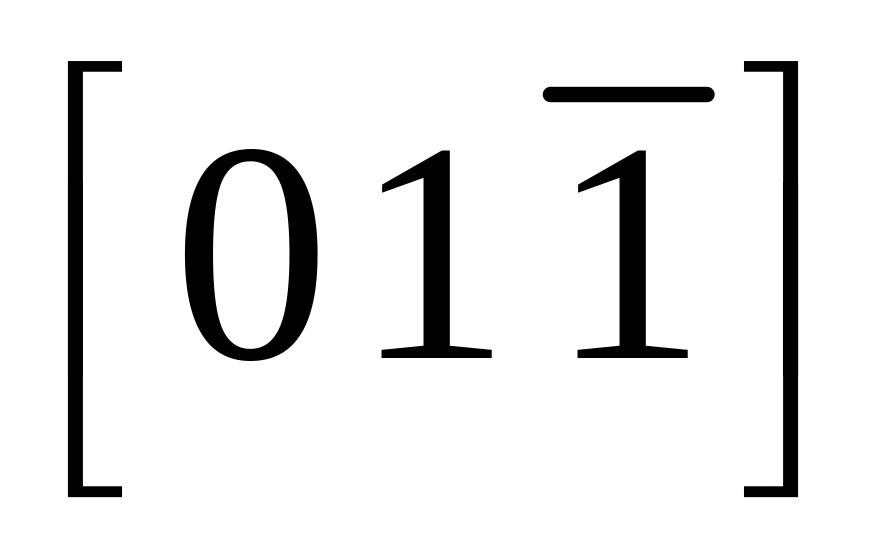 .
За оси координат приняты кристаллографические
оси кубического кристалла:
.
За оси координат приняты кристаллографические
оси кубического кристалла:
а) Выпишите компоненты тензора деформации сдвигом.
б) Выпишите компоненты тензора чистой деформации, если скольжение на величину α` происходит в том же направлении , но по плоскости (100). [16]
На тетрагональный кристалл действуют растягивающее напряжение σ вдоль [100] и сдвиговое напряжение τ по (100) вдоль [010].
а) Выпишете компоненты тензора напряжений, отнесенные к кристаллографическим осям.
б)
Найдите сдвиговое напряжение по (110) в
направлении
![]() ,
изменив оси тензора напряжений.
,
изменив оси тензора напряжений.
в) Таким же способом найдите растягивающее напряжение, нормальное к (110) [16].
Используя соотношение Шмида, определить сдвиговые касательные напряжения для всех СС ГЦК (ОЦК, ГПУ) кристалла, если компоненты тензора напряжений в декартовой ортогональной системе координат, совпадающей с кристаллографической системой кубических кристаллов (для ГПУ ось Ох1 направлена вдоль [2
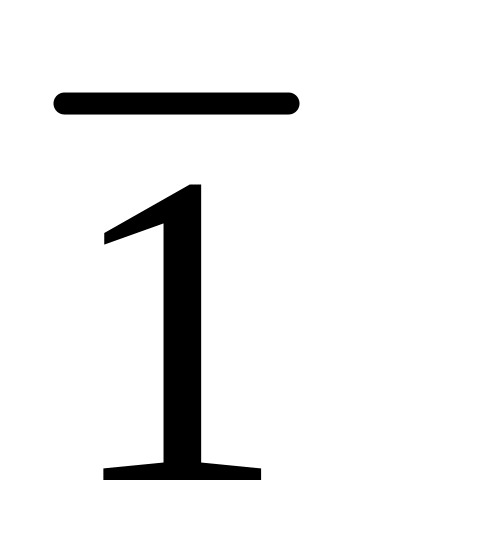 0],
ось Ох2
–
перпендикулярна ей и лежит в базовой
плоскости, ось Ох3
–
вдоль [0 0 0 1]), имеют вид:
0],
ось Ох2
–
перпендикулярна ей и лежит в базовой
плоскости, ось Ох3
–
вдоль [0 0 0 1]), имеют вид:
а) σ11=σ22=σ33=σ, σij=0 при i≠j – всестороннее растяжение (сжатие);
б) σ11=σ, остальные σij=0 – одноосное растяжение (сжатие);
в) σ12=σ21=τ, остальные σij=0 – простой сдвиг;
г) σ11=A, σ22=B, σ33=C, σij=0 при i≠j – напряженное состояние общего вида в главных осях тензора напряжений.
Показать, что в вершинах текучести для ГЦК кристаллита критерий Шмида одновременно выполняется или для 6, или для 8 СС.
Кубический кристалл растягивается в направлении [100]. Его деформация создается краевыми дислокациями, параллельными [001] и скользящими по плоскостям (110) и
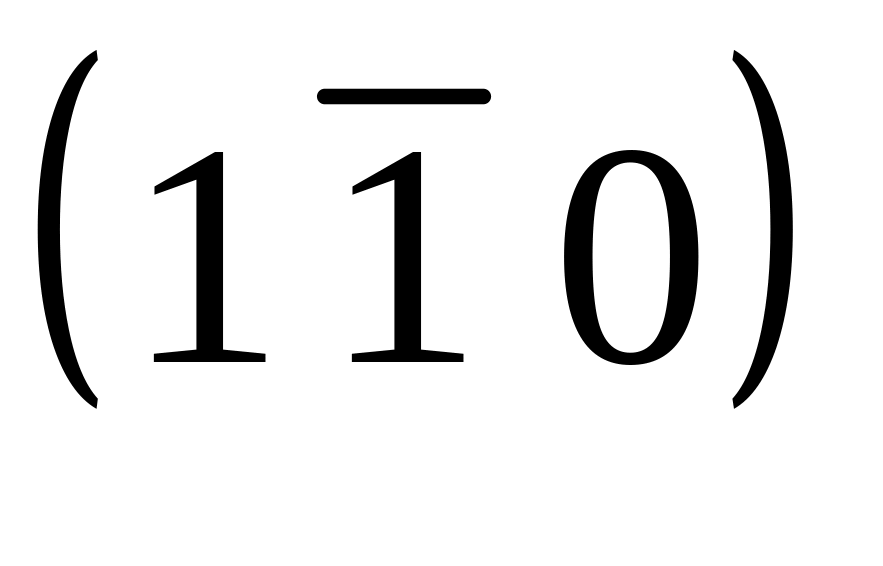 .
Если плотность этих дислокаций равна
ρ, величина вектора Бюргерса каждой b
и их средняя скорость v,
определите скорость возрастания
деформации растяжения кристалла (равную
(1/l)(dl/dt),
где l
– длина кристалла в направлении
растяжения) [16].
.
Если плотность этих дислокаций равна
ρ, величина вектора Бюргерса каждой b
и их средняя скорость v,
определите скорость возрастания
деформации растяжения кристалла (равную
(1/l)(dl/dt),
где l
– длина кристалла в направлении
растяжения) [16].Имеется две бесконечно длинные ортогональны винтовые дислокации с векторами Бюргерса b1 и b2. Рассчитайте величину силы, с которой вторая дислокация действует на первую [16].
Если концентрация вакансий в алюминии при его температуре плавления составляет 9,4·10-4 и если после закалки алюминия от температуры плавления вакансии конденсируются в диски на плотноупакованных плоскостях и образуют петли Франка, определите плотность создающихся дислокаций при радиусе петель а) 50 Å и б) 500 Å [16].
Один из способов описания взаимной ориентации сдвойникованной области и матрицы в двойниках (1-го рода) заключается в определении угла поворота решетки сдвойникованного индивида вокруг оси, лежащей в плоскости двойникования K1 перпендикулярно направлению сдвига η1. Определите величину угла поворота в случае двойника в а) ОЦК, б) ОЦК и г) ГПУ материалов [16].
Двойник в ОЦК-металле имеет следующие элементы двойникования: K1 = (112),
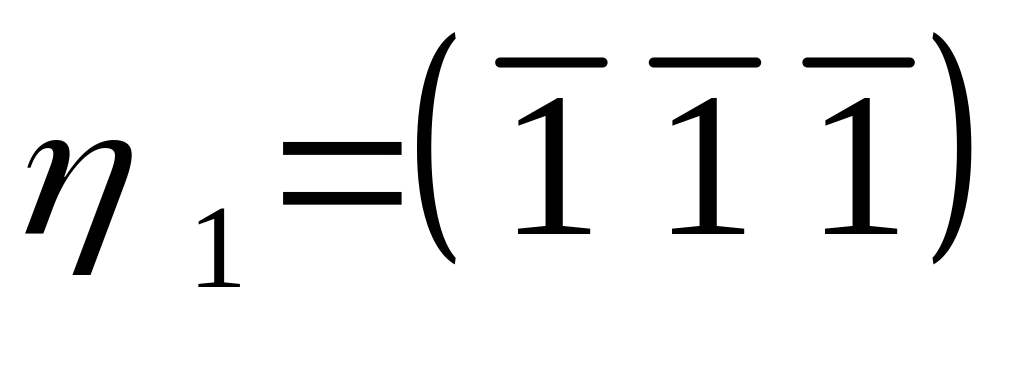 [16].
[16].
а) Определите индексы Миллера плоскостей, в которые преобразуются под действием двойникового сдвига следующие кристаллографические плоскости: (001), (010), (100).
б) Выведите тензор преобразования индексов плоскостей и определите плоскость, в которую переходить плоскость (101).
Показать, что критерий Шмида соответствует критерию Треска.
Показать, что первый инвариант линейной комбинации
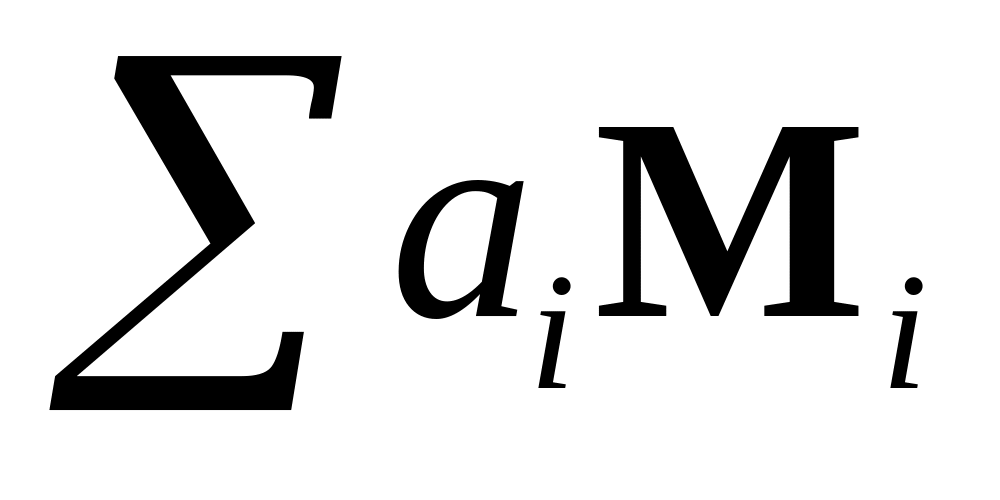 равен 0.
равен 0.Записать тензор пластической деформации при деформировании кристалла сдвигом краевых дислокаций по СС [110]
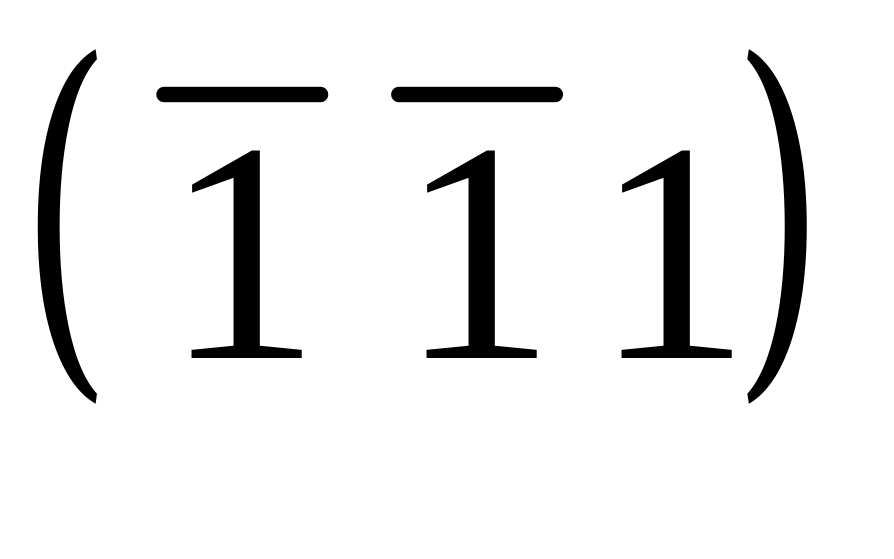 .
.Определить величину сдвига двойника γtw ГЦК, ОЦК и ГПУ металлов.
Используя соотношение , записать в общем виде неупругую составляющую тензора деформации скорости, связанную с двойникованием.
Используя разложение , полярное разложение , малость упругих деформаций показать, что тензор спина решетки при квазистатическом нагружении определяется согласно соотношению .
Показать, что если кристалл идеально ориентирован для сдвига по одной системе скольжения, то поворот решетки согласно модели Тейлора отсутствует, несмотря на формоизменение зерна.
Показать, что с точки зрения линейного программирования модели Тейлора и Бишопа-Хилла двойственны.
Из опыта решения задач МСС (и МДТТ, в частности) представляется обоснованным переход от трехмерных задач к двумерным для качественного анализа поведения исследуемых систем [1]). Конечно, в природе не существует двумерных или плоских кристаллов. Однако подобный кристалл является удобным модельным материалом для анализа физических моделей пластичности поликристаллических материалов. Отдельные эффекты реальных кристаллов, по-видимому, описать двумерной моделью принципиально невозможно. Между тем закономерности пластического поведения двумерных кристаллов должны в определенной степени наблюдаться и у реальных кристаллов.
Определить рабочую плоскость для 2Д-моделирования ГЦК-кристалла с учетом сдвигов по трем СС: линии краевых дислокаций из этих СС ГЦК-кристалла ортогональны плоскости моделирования, векторы Бюргерса и нормали к плоскостям скольжения лежат в плоскости моделирования.
Совпадает ли плоскость моделирования с плоскостью (111) наиплотнейшей упаковки ГЦК-кристалла?
Реализовать для плоского кристалла, соответствующего ГЦК-кристаллу (в 2Д-модели имеются 3 системы скольжения, векторы Бюргерса и нормали лежат в плоскости моделирования), следующие физические модели:
а) Закса,
б) Линя,
в) Тейлора,
г) Бишопа–Хилла.
С использованием построенных моделей проанализировать различные процессы деформирования.
Определить рабочую плоскость для 2Д-моделирования ОЦК-кристалла с учетом сдвигов по СС: линии краевых дислокаций из этих СС ГЦК-кристалла ортогональны рабочей плоскости, векторы Бюргерса и нормали к плоскостям скольжения лежат в плоскости моделирования. Определить число возможных направлений скольжения.
Реализовать для плоского кристалла, соответствующего ОЦК-кристаллу (в 2Д-модели векторы Бюргерса и нормали лежат в плоскости моделирования), следующие физические модели:
а) Закса,
б) Линя,
в) Тейлора,
г) Бишопа–Хилла.
С использованием построенных моделей проанализировать различные процессы деформирования.
Реализовать модель Закса для ГЦК-поликристалла. Определить предел текучести при одноосном растяжении, если критическое напряжение сдвига для всех СС равняется (для меди = 15 МПа).
Реализовать модель Закса для ОЦК-поликристалла. Определить предел текучести при одноосном растяжении, если критическое напряжение сдвига для всех СС равняется .
Исследовать начальную поверхность текучести ГЦК-монокристалла, используя в качестве критерия начала пластического деформирования критерий Шмида: определить число ребер, вершин различного порядка (который определяется числом одновременно активных СС), интенсивность напряжений в вершинах высокого порядка. В частности, убедиться, что критерий Шмида не может одновременно выполняться ровно на пяти СС.
Аналогично упр. 38 выполнить соответствующие исследования начальной поверхности текучести ОЦК-монокристалла.
Исследовать начальную поверхность текучести ГЦК-монокристалла, используя в качестве критерия начала пластического деформирования критерий Шмида: определить при различных ориентировках монокристалла на скольких СС (и на каких) будет впервые выполнен критерий текучести при монотонном растяжении ГЦК-монокристалла от естественной конфигурации.
При одноосном растяжении ГЦК-монокристалла в случае специальной ориентировки – при нахождении оси растяжения в вершине стереографического треугольника [0 0 1] (при рассмотрении обращенного движения) – все СС равноправны, т.е. должны быть приняты активными и скорости сдвигов по ним должны совпадать. Убедиться, что в этом случае согласно исходной модели стесненного поворота Тейлора (
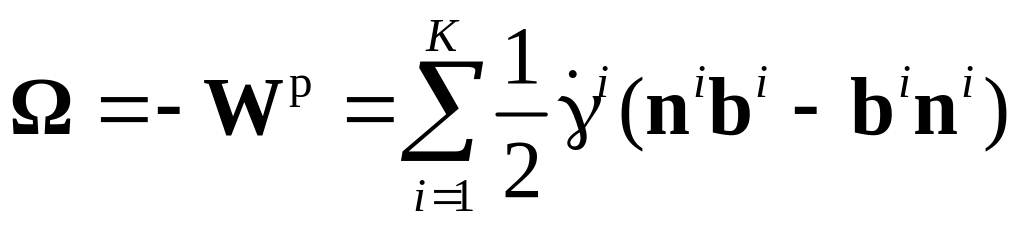 ,
K
– число СС), спин решетки Ω
нулевой, в то время как при ограничении
числа активных СС пятью (согласно
моделям типа Тейлора – Бишопа – Хилла)
спин решетки Ω
различен
в зависимости от выбора активных СС.
,
K
– число СС), спин решетки Ω
нулевой, в то время как при ограничении
числа активных СС пятью (согласно
моделям типа Тейлора – Бишопа – Хилла)
спин решетки Ω
различен
в зависимости от выбора активных СС.Реализовать для ГЦК (ОЦК, ГПУ) кристалла вязкоупругую модификацию модели Линя, используя соотношение . Исследовать вопрос об эквивалентности вязкоупругой и жесткопластической моделей.
Реализовать для ОЦК (ГЦК, ГПУ) кристалла вязкопластическую модификацию модели Линя, используя соотношение . Исследовать вопрос об эквивалентности вязкопластической и жесткопластической моделей.
Реализовать для ГПУ (ГЦК, ОЦК) кристалла упруговязкопластическую модификацию модели Линя, используя соотношение . Исследовать эффект «нырка» интенсивности напряжений.
Показать справедливость соотношений и .
Проверить справедливость соотношения .
Показать, что π, определяемый соотношением , является тензором четвертого ранга.
Реализовать модель мезоуровня неупругого деформирования ГЦК, ОЦК, ГПУ кристаллита.
Реализовать двухуровневую модель неупругого деформирования ГЦК, ОЦК, ГПУ поликристалла с учетом согласования ОС масштабных уровней.
