8.4. Модель поворотов кристаллической решетки, учитывающая взаимодействие элементов мезоуровня

Как уже отмечалось выше (см. п. 3.4), наиболее распространенными среди исследователей моделями повоторов кристаллической решетки зерен (далее используется термин «ротации») являются две: модель «полностью стесненного» поворота по Тейлору и модель так называемого «материального поворота» . В качестве серьезного недостатка этих моделей следует отметить отсутствие в них учета микровзаимодействий соседних зерен в поликристалле; по существу, взаимодействие кристаллитов осуществляется на макроуровне за счет используемой гипотезы связи уровней (Фойгта, Рейсса и др.). При рассмотрении поликристаллических материалов, для которых можно пренебречь взаимодействием дислокаций в соседних зернах, например, при наличии «толстых» границ аморфного строения в полимерных полукристаллических материалах, применение данных моделей достаточно обосновано. Однако для металлов экспериментально подтверждено (например, в работах В.Е.Панина [54], В.В.Рыбина [34]), что существенную роль в поворотах решетки играет несовместность скольжения дислокаций в соседних зернах.

Вообще говоря, в литературе можно найти достаточно много работ по физическим теориям (в иностранной литературе – crystal plasticity), в которых так или иначе вводятся вращательные степени свободы для кристаллической решетки и строятся кинетические уравнения для поворотов. К принципиальным сложностям таких моделей следует отнести как физическую непрозрачность описания поворотов и причин, приводящих к ним, так и неучет влияния на разворот данного зерна несовместности движения дислокаций в рассматриваемом и в соседних зернах. К одной из немногих работ по физическим теориям пластичности, в которых рассматривается вопрос описания разворотов в поликристалле при помощи явного введения моментных напряжений, относится работа [111], кратко изложенная в п.3.3. Анализируя рассмотренную работу, остановимся на тех моментах, которые не позволяют использовать ее в данном исследовании:

• в работе не приводится физическое обоснование соотношения для моментных напряжений, неявно предполагается независимость моментных напряжений от несовместности пластических деформаций в соседних зернах, не указывается физический объем, к которому приложены моментные напряжения;

• рассматривается поворот, связанный с мгновенной скоростью вращения материальных отрезков, в данный момент образующих ортогональную тройку, совпадающую с главными осями меры скорости деформации, пренебрегается упругими искажениями решетки;

• не учитывается пороговость необратимых разворотов, что приводит к появлению поворотов элементов уже при малых деформациях.

Введем дополнительные термины, необходимые для описания эволюционирующей структуры поликристалла, которые будут использоваться в дальнейшем. Под «элементом ротации» (ЭР) будем понимать любую структурную составляющую микроструктуры (зерно, субзерно, фрагмент) или их совокупность, способную к разворотам как целое, с сохранением (с приемлемой точностью) правильного кристаллического строения решетки составляющих, их взаиморасположения и взаимоориентации (рис.8.4.1). Здесь следует отметить, что, вообще говоря, размер ЭР, претерпевающего разворот, заранее не известен. Более того, эксперименты показывают, что с увеличением интенсивности деформаций характерные размеры разворачивающихся элементов структуры изменяются [10, 28, 34]. Для определения ЭР в каждый момент деформирования в работе вводится еще один тип структурных элементов, которые в каждый момент деформирования могут образовывать ЭР (по определенному алгоритму, о котором будет сказано ниже). Под «зерном» будем понимать наименьший объем материала, который (по крайней мере, на начальный момент деформирования) с приемлемой точностью можно считать монокристаллическим телом. Под «фрагментами зерна» будем понимать микрообласти материала, разориентированные относительно друг друга на углы порядка нескольких минут или градусов [34]. Надо отметить, что введение понятия «элемент ротации» не подменяет понятий «зерно» и «фрагмент зерна», т.к. вообще говоря, в произвольный момент деформирования в качестве ЭР могут выступать и фрагмент, и группа фрагментов, и зерно (и даже совокупность зерен).

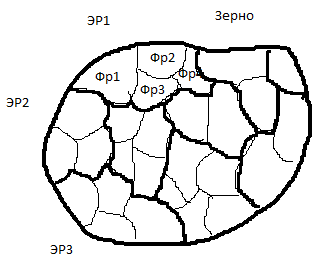
Рис.8.4.1. К выделению структурных элементов

В работах [40, 41] одной из причин разворотов решетки зерен (кроме т.н. «материального» поворота) считается несовместность сдвигов по системам скольжения в соседних зернах (моделирующих, в свою очередь, движение дислокаций). Тогда скорость изменения вектора поверхностного момента, действующего на часть границы анализируемого зерна (фрагмента зерна) в результате сопротивления переходу дислокаций из анализируемого зерна (фрагмента) в соседние ( ), можно определить как сумму

,

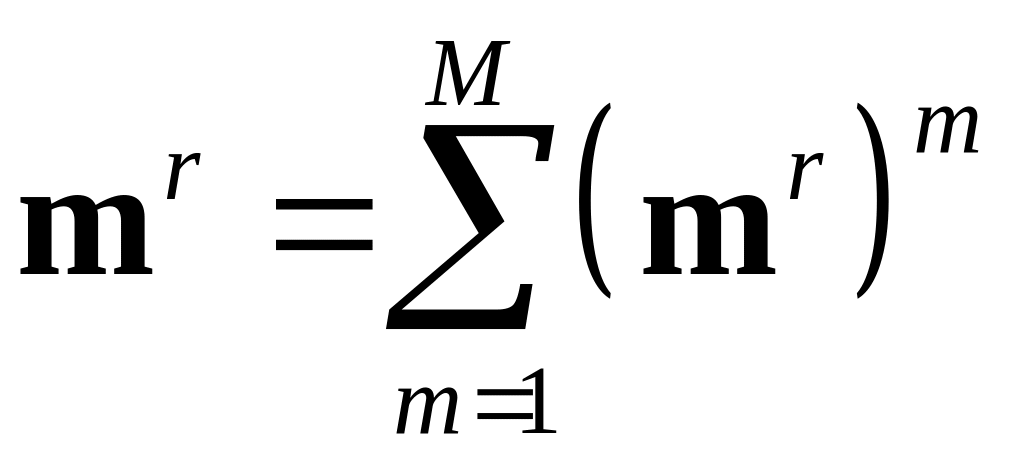где – соответствующая коротационная производная (вопрос о ее выборе обсуждается ниже), – составляющая скорости вектора момента, обусловленная несовместностью сдвига в данном фрагменте со сдвигами в соседнем m-м фрагменте, М – число соседних фрагментов.

Эволюция вектора-момента определяется следующим соотношением:

,

где λ – экспериментально определяемый (в ) параметр, – внешняя для анализируемого фрагмента единичная нормаль к границе с соседним фрагментом, – скачок пластической составляющей градиента скорости, определяемый согласно соотношению

,

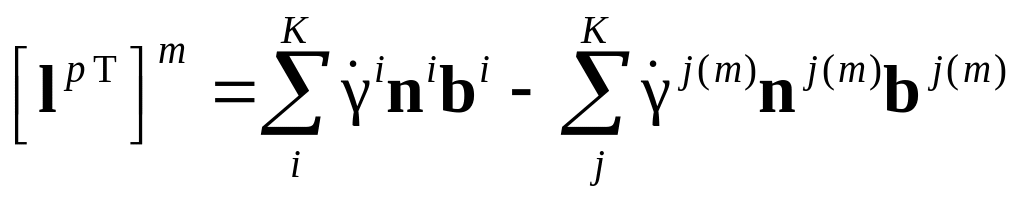где , – скорости сдвигов, , – единичные векторы по направлениям векторов Бюргерса, , – нормали для систем скольжения в исследуемом и соседнем фрагментах соответственно, – число систем скольжения (для ГЦК кристалла с учетом удвоения – 24).

Вкратце проанализируем соотношение, следующее из – :

.

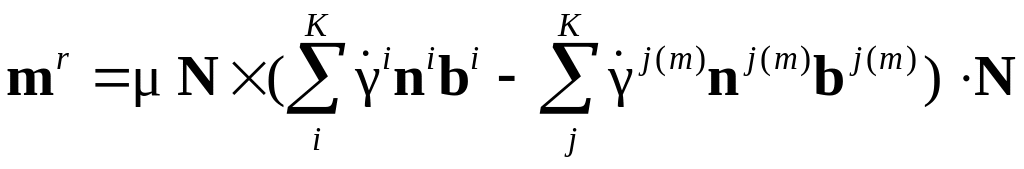1. В соотношении явно учитывается несовместность сдвигов и ориентация границы.

2. Рассмотрим случай отсутствия сдвигов в соседнем зерне (что согласно модели эквивалентно нахождению зерна в жесткой оболочке). Для простоты будем рассматривать случай, когда активна одна СС (индекс отбросим). Тогда .

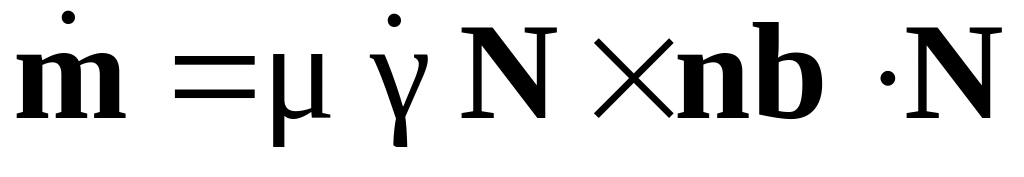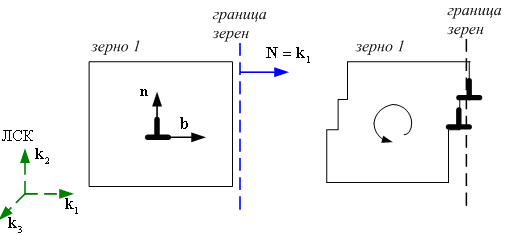
Рис. 8.4.2. Схема для пояснения , ,

Например, для случая, изображенного на рис. 8.4.2, . При в верхней части границы вследствие прохождения дислокаций по СС возникает избыток атомов, в нижней части – недостаток, поэтому скорость момента направлена против часовой стрелки.

3. Векторную часть , порождаемую операцией векторного умножения « 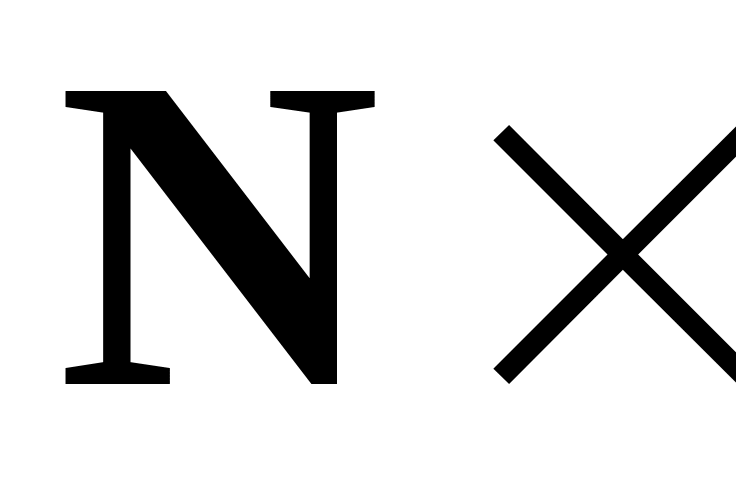» можно трактовать как вектор линии дислокации ориентационного несоответствия [34], залегающей в границе. Логично, что скорость момента, действующего на зерно, направлена вдоль этой линии.

4. Скалярные произведения « » характеризуют, каким образом сдвиг по СС ориентирован по отношению к границе. Например, в случае, когда направление сдвига по СС перпендикулярно нормали к границе, соответствующая составляющая будет нулевой, что согласуется с физическим анализом.

Соотношение перекликается с приведенным в работе [34]

,

где – вектор разориентации, - длина дуги деформации, – нормаль к границе между зернами n и n’, 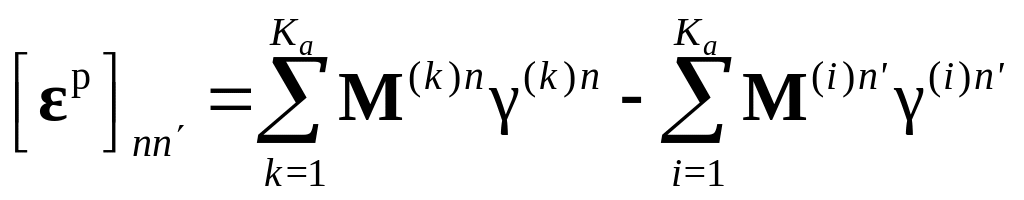– разность пластических составляющих деформаций в зернах n и n’. Однако имеется ряд отличий между предлагаемым соотношением и содержащимся в цитируемой работе :

– в соотношении используется симметричный тензор деформации, что представляется не совсем корректным с точки зрения описания движения дислокаций (вторая часть ориентационного тензора не соответствует реальной СС),

– соотношение не предполагает пороговости: изменение вектора начинается, как только начинается пластическое деформирование в соседних зернах, что также не соответствует физике процесса. Для обеспечения пороговости «решеточного» поворота вводится силовой фактор – моментные напряжения, чтобы затем явно задать критерий реализуемости решеточного поворота в замыкающем уравнении для связи спина решетки с моментными напряжениями.

При этом стоит отметить, что в работе [34] делается попытка обоснования соотношения на основе физических и математических посылок: вводятся дислокации ориентационного несоответствия, тензор их плотности , выводится уравнение для изменения в зависимости от деформации, затем автор приходит к соотношению . Соответствующие выкладки были проведены как для соотношения , так и для соотношения . Несмотря на ряд возникших при этом вопросов, такой путь – построение феноменологических моделей путем анализа физики процесса на меньших масштабных уровнях – представляется продуктивным.

Определим вид коротационной производной, которую необходимо применить в соотношениях – для соблюдения принципа материальной индифферентности. Пусть на элемент ротации, а также на все фрагменты, которые его окружают, накладывается поворот как жесткого целого. В этом случае очевидно, что и вектор (тензор) момент моментных напряжений испытает такой же поворот. Также отметим, что при расчетах для отдельного фрагмента все величины (деформации скорости, напряжения, тензор упругих свойств, сдвиги по системам скольжения, моменты) определяются с точки зрения наблюдателя, находящегося в кристаллографической системе координат; к этой же системе координат жестко «привязан» материал фрагмента. Т.к. вращение КСК осуществляется по отношению к лабораторной системе координат (ЛСК) как жесткого целого (вместе с материалом), то для удовлетворения принципа материальной индифферентности необходимо выбрать тип коротационной производной, «привязанной» к угловой скорости вращения кристаллической решетки, следовательно:

,

где – тензор спина кристаллической решетки фрагмента, определяемый в каждый момент деформирования как тензор, ассоциированный с вектором угловой скорости вращения решетки , , – тензор Леви–Чивита.

Тогда окончательно для поверхностных моментов имеем:

.

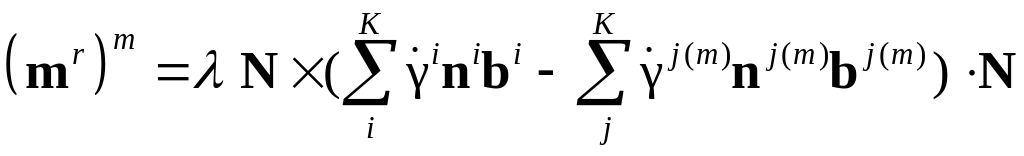Результирующий вектор-момент равен:

,

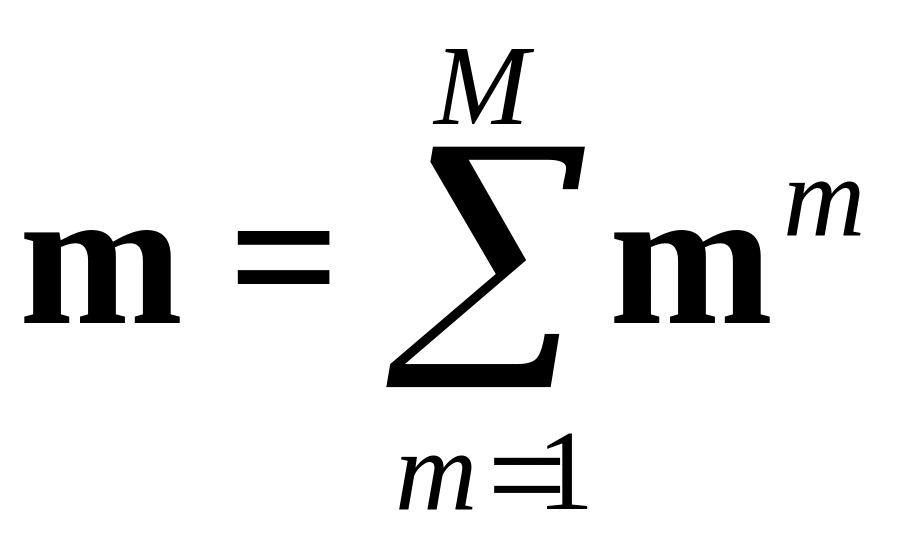где по индексу нумеруются составляющие момента на отдельных фасетках данного элемента ротации (кристаллита).

Скорость поворота (спин) решетки представляется суммой двух составляющих. Первая составляющая описывает поворот решетки вместе с материалом зерна при наложенном кинематическом воздействии, назовем эту составляющую «материальным поворотом». Связывая материальный поворот с ортогональным тензором, сопровождающим упругую деформацию, данную составляющую предлагается определять как . Вторая составляющая скорости поворота («решеточный поворот») характеризует ротацию собственно решетки кристаллита, обусловленную взаимодействием с окружением.

Составляющая спина решетки определяется соотношением:

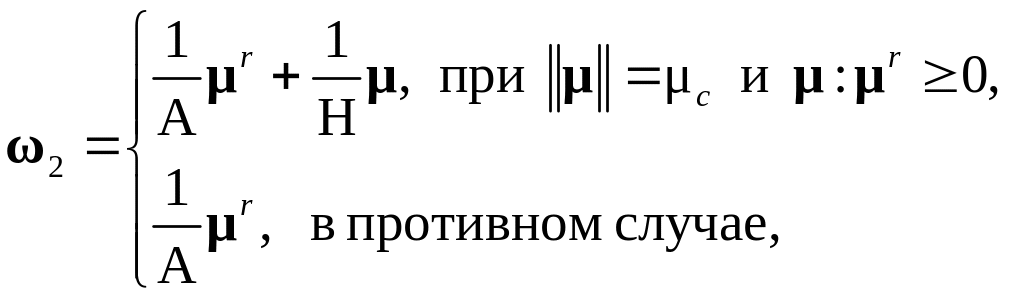
где – интенсивность тензора моментных напряжений, 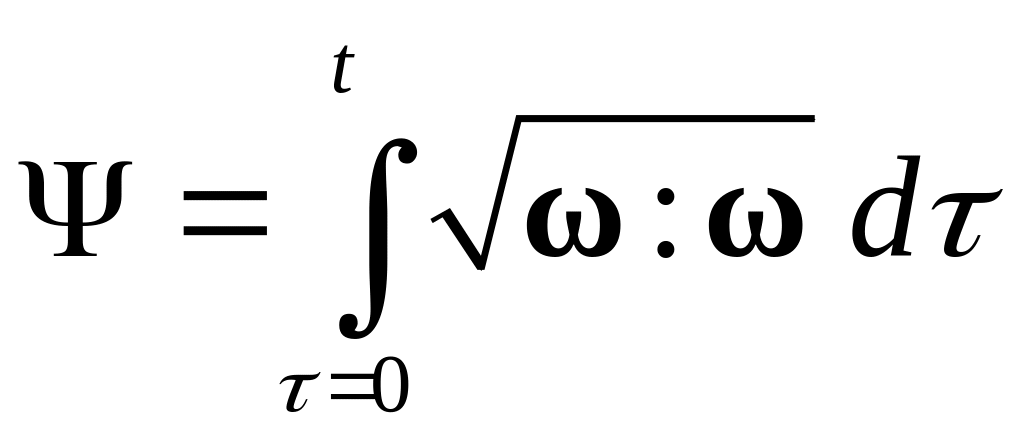– накопленный решеточный поворот, – текущее критическое моментное напряжение, определяемое экспериментально. Тензор моментных напряжений ассоциирован с вектором поверхностного момента ( ).

Согласно , составляющая спина решетки характеризует вращение решетки кристаллита, инициированное несовместностью движения дислокаций в соседствующих кристаллитах.