8.3. Классификация внутренних переменных и уравнений конститутивной модели на примере двухуровневой упруговязкопластической модели

На макроуровне рассматривается представительный объем поликристаллического металла, состоящий из совокупности кристаллитов – элементов мезоуровня.

Конститутивная модель материала на макроуровне принимается в виде:

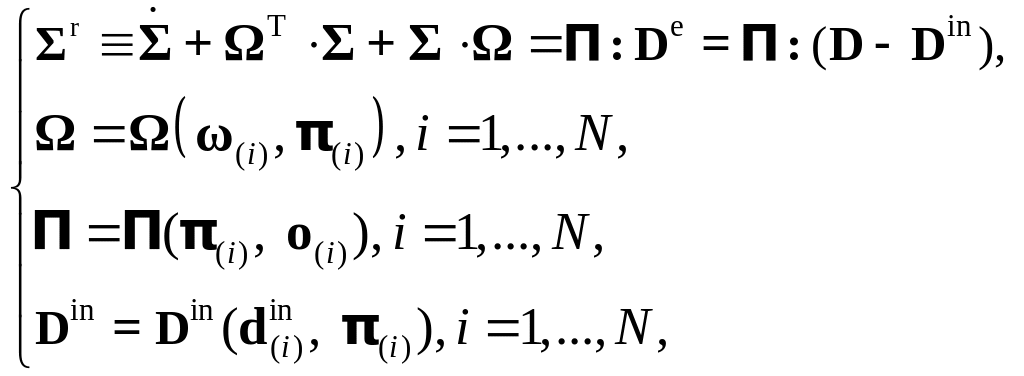
где – тензор напряжений Коши, Π – тензор модулей упругости, D, – тензор деформации скорости, его упругая и неупругая составляющая, индекс «r» означает независящую от выбора системы отсчета производную, – тензор, описывающий движение подвижной системы координат, относительно которой определяется собственно деформационное движение [31] на макроуровне. Стоит акцентировать внимание на том, что вопрос однозначного введения независящей от выбора системы отсчета производной, т.е. корректного разложения движения на квазитвердое и собственно деформационное – один из наиболее трудных в нелинейной механике деформируемого твердого тела [31] и, по мнению авторов, не решен до сих пор. Для определения предлагается использовать условие согласования определяющих соотношений на различных масштабных уровнях.

Таким образом, неупругая составляющая деформации скорости , эффективные анизотропные упругие свойства Π и описывающий движение подвижной системы координат тензор Ω являются явными внутренними переменными модели макроуровня, в каждый момент зависят от структуры на низших масштабных уровнях (а через нее – от истории нагружения) и определяются с помощью модели мезоуровня ( – число элементов мезоуровня, необходимых для статистического описания представительного объема макроуровня, далее индекс элемента мезоуровня опускается). Параметры представляют собой неявные внутренние переменные макроуровня.

Согласно вышеприведенной общей структуре конститутивной модели ₁ является уравнением состояния, а ₂-₄ – замыкающими уравнениями, конкретизация которых является одной из основной целей работы (предлагаемый авторами подход описан в п 8.2); в качестве эволюционных уравнений выступают соотношения модели мезоуровня.

На мезоуровне (уровне кристаллита) в двухуровневых моделях неупругого деформирования поликристаллических металлов используется следующая система соотношений:

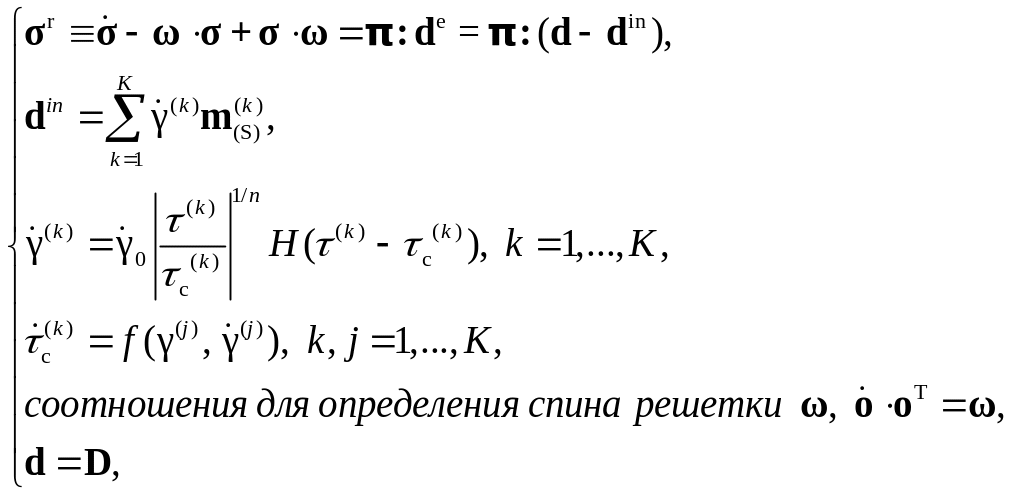
где – тензор напряжений Коши,π– тензор четвертого ранга упругих свойств кристаллита, – тензор деформации скорости, его упругая и неупругая составляющие на мезоуровне и тензор спина КСК, параметры являются явными внутренними переменными мезоуровня,

– накопленный сдвиг и критическое напряжение сдвига по k-й системе скольжения, – симметричная часть ориентационного тензора k-й системы скольжения, , – единичные векторы в направлении вектора Бюргерса и нормали к плоскости скольжения; плоскости залегания и ориентация векторов Бюргерса, вдоль которых осуществляется трансляционное движение (скольжение) краевых дислокаций, известны, ими являются наиболее плотно упакованные плоскости и направления; так, в ГЦК–металлах скольжение краевых дислокаций осуществляется в плоскостях системы 111 по направлениям 110 [42],

– константы материала: характерная скорость сдвигов при равенстве касательных напряжений на СС критическим и константа скоростной чувствительности материала [68],

– действующее в k-й системе скольжения касательное напряжение, ,

– функция Хэвисайда,

– число систем скольжения для рассматриваемого типа решетки. Отметим, что число систем скольжения в данном случае равно удвоенному числу кристаллографических систем (в каждой плоскости противоположным направлениям вектора Бюргерса соответствуют разные системы скольжения), т.е., например, для ГЦК–кристалла рассматривается 24 системы скольжения,

о – тензор текущей ориентации кристаллографической системы координат кристаллита относительно фиксированной лабораторной системы координат. Скорости сдвигов, накопленные сдвиги, критические напряжения систем скольжения, ориентационный тензор КСК кристаллита являются неявными внутренними переменными мезоуровня.

В качестве определяющего соотношения (уравнения состояния) на мезоуровне выступает закон Гука в скоростной форме ₁, при этом учитывается геометрическая нелинейность: квазитвердое движение [31] связывается с поворотом решетки (кристаллографической системы координат); в коротационной производной тензора напряжений Коши фигурирует тензор спина , характеризующий скорость вращения кристаллической решетки. Таким образом, напряжения характеризуют именно упругие связи в зерне, связанные с изменением расстояний между соседними атомами. Различные модели поворота решетки подробно рассмотрены в п.3.4 (см. также [57]).

Уравнение ₂ – кинематическое соотношение, согласно которому неупругое деформирование кристаллита осуществляется за счет сдвигов по системам скольжения.

Для определения скорости неупругого деформирования в моделях поликристаллических металлов может быть использована [52, 53] либо упругопластическая модель на базе модели Линя [21, 38, 42], либо применяемая в настоящей работе упруговязкопластическая модель ₃, в которых (как и ) связывается со скрытыми внутренними переменными мезоуровня, характеризующими дислокационное скольжение – скоростями сдвигов по системам скольжения, (K – число систем скольжения для рассматриваемого типа решетки), критическими напряжениями , тензором о текущей ориентации кристаллографической системы координат зерна относительно фиксированной лабораторной системы координат. Уравнение ₄, описывает эволюцию критических напряжений сдвига по системам скольжения.

Для передачи воздействия, производимого на макроуровне, на низшие масштабные уровни в модели применяется гипотеза Фойгта, согласно которой тензоры деформации скорости для каждого кристаллита совпадают с тензором деформации скорости макроуровня .

В конститутивной модели мезоуровня соотношения ₁ – уравнение состояния, ₃ – ₄ – эволюционные уравнения, в качестве замыкающих выступают уравнения ₂, ₅. Классификация внутренних переменных макро- и мезоуровня сведена в таблице 8.3.1.

Таблица 8.3.1

Параметры конститутивной модели поликристаллических металлов на разных масштабах

	Параметры воздействия	Параметры, определяемые на данном масштабном уровне
		Явные внутренние переменные	Неявные внутренние переменные	Реакция материала
Макроуровень			(для каждого кристаллита)
Мезоуровень (для каждого кристаллита)