Вопросы к главе 7

1. Какие модели физических теорий пластичности можно отнести к классу упруговязкопластических?

2. Проведите анализ мультипликативного разложения градиента места Ли с позиций преобразования материальных бесконечно малых отрезков из отсчетной конфигурации. Как определяется промежуточная конфигурация?

3. Запишите соотношения для определения неупругих составляющих тензоров деформации скорости и вихря через скорости сдвигов.

4. Выведите соотношение для связи упругих составляющих тензоров деформации скорости и скорости деформаций Коши ‑ Грина.

5. Какие материалы называются упругими по Грину? Каков физический смысл упругого потенциала?

6. Приведите определение операции позиционного умножения. Докажите, что объект, получаемый с помощью этой операции, является тензором, определите его ранг.

7. Проверьте выполнение аксиом ТОС для соотношения .

8. Приведите физические соотношения для скоростей сдвигов (за счет скольжения дислокаций).

9. Приведите кинематические и определяющие соотношения для кристаллита, применяемые в упруговязкопластических моделях.

10. Предложите алгоритм численной реализации упруговязкопластической модели кристаллита.

11. Проанализируйте известные Вам законы упрочнения. Проведите их сравнительный анализ.

12. Приведите соотношения для связи тензора напряжений Коши, взвешенного тензора Кирхгоффа, первого и второго тензоров Пиола ‑ Кирхгоффа, установите их физический (энергетический) смысл.

13. Приведите соотношения, используемые для осреднения напряжений в модели [64], проведите их анализ.

14. Какие гипотезы могут быть использованы для удовлетворения условий совместности деформаций кристаллитов?

15. Проанализируйте модель «механического порогового напряжения» (MTS – mechanical threshold stress), предложенной Фоллансби и Куксом. Укажите недостатки этой модели.

16. Перечислите известные Вам модели ротации решетки. Как согласно им преобразуется векторы, задающие СС (n^(k), b^(k))? Используя какое предположение, можно записать соотношения:

?

17. Проведите физический анализ соотношения для определения скоростей сдвигов .

18. На основе какого подхода построена модель E.P. Busso & G. Cailletaud?

19. Изложите суть модели «текстурных компонентов».

20. В чем состоят основные отличия градиентных физических теорий от классических?

21. Сформулируйте основные положения модели «структурных элементов».

Глава 8. Структура и алгоритмы реализации многоуровневых моделей

8.1. Наиболее распространенная схема построения многоуровневых моделей, их структура и классификация

С конца 70-х – начала 80-х прошлого столетия начинаются интенсивные исследования текстурообразования и влияния текстуры на свойства материалов с применением как физических теорий пластичности, так и экспериментальных методов [9, 77, 175 и др.]; краткий обзор способов описания текстуры и современные эффективные методы описания интересующийся читатель может найти, например, в [153]. Обширный обзор экспериментальных данных, теоретических методов и результатов анализа текстурообразования (главным образом – в процессах прокатки) с 60-х годов ХХ века по настоящее время содержится в статье [123]; особое внимание уделяется механизмам формирования в ГЦК–металлах двух типов текстуры прокатки – «текстуры меди» и «текстуры латуни».

Классификационными признаками для подразделения многоуровневых моделей на классы могут быть выбраны а) число уровней, включенных в рассмотрение, и связанный с уровнями выбор «элементарной ячейки» (в дальнейшем будем называть ее «элементом»); б) модель (гипотеза) связи однотипных характеристик различных уровней; в) физические теории, положенные в основу нижних масштабных уровней. В настоящее время подавляющее большинство используемых многоуровневых моделей относятся к двухуровневым (макро- и мезоуровни), в качестве элемента мезоуровня в таких моделях, как правило, выбирается зерно; в последние годы появляются трехуровневые модели (с добавлением микроуровня).

При моделировании конкретного процесса число рассматриваемых уровней определяется исследователем. Например, при моделировании неупругого деформирования поликристаллических металлов иерархию масштабных уровней можно определить следующим образом: макроуровень – мезоуровень (уровень кристаллита (зерна, субзерна, фрагмента)) – микроуровень (дислокационная структура) (рис. 8.1). Следует отметить, что на макроуровне следует выделить подуровень представительного макрообъема, которым исследователи оперируют при формулировке конститутивной модели материала, и уровень макроконструкции, реального физического тела, обрабатываемой заготовки и т.д., для которых требуется ставить и решать соответствующую краевую задачу. В настоящей работе внимание будет сосредоточено именно на подуровне представительного макрообъема.

Рис. 8.1.1. Схематичное представление иерархии масштабных уровней при моделировании поликристаллических металлов (слева направо: макроуровень, мезоуровень, микроуровень)

О гипотезах связи однотипных переменных разных уровней

Весьма важным отличительным признаком многоуровневых моделей, во многом определяющим «качество» моделей, является гипотеза о связи характеристик различных уровней (иногда говорят о гипотезе осреднения, или о гипотезе агрегирования – «объединения» элементов нижележащего уровня в элемент более высокого масштабного уровня). Наиболее распространенной в ФТП является гипотеза Фойгта (в некоторых работах ее называют гипотезой Тейлора), согласно которой полные деформации (или деформации скорости) зерен, входящих в поликристаллический агрегат, полагаются равными деформации (деформации скорости) представительного макрообъема, задаваемой условиями нагружения или решением соответствующей краевой задачи. Иначе говоря, передача воздействий с макроуровня на мезоуровень при принятии этой гипотезы осуществляется кинематическим способом.

Другой распространенной гипотезой является гипотеза Рейса (называемая в некоторых работах гипотезой Закса), в соответствии с которой однородными по поликристаллическому агрегату являются напряжения. Таким образом, применение этой гипотезы соответствует силовому (статическому) способу передачи воздействий.

Гипотеза Фойгта дает так называемую верхнюю оценку (интенсивность напряжений получается наибольшей из всех гипотез), гипотеза Рейса – нижнюю оценку. Следует отметить, что применение той или иной модели связи уровней может вести к качественно отличающимся результатам; так, в работе [123] указывается, что применение гипотезы Фойгта при исследовании процесса прокатки дает текстуру меди, а гипотезы Рейсса – текстуру латуни. Конечно, ни одна их этих гипотез не отражает реальные взаимодействия зерен в поликристалле. При этом в таких моделях обычно не учитывается взаиморасположение элементов–зерен в поликристалле. В связи с этим значительное число статей посвящено поиску новых способов соединения подмоделей монокристаллов в модель поликристалла. Согласно одному из таких способов параметры процесса предлагается усреднять по результатам расчета с применением каждой из указанных гипотез по отдельности. В работе [139] вводится взвешенное осреднение всех параметров процесса (напряжений, деформаций скорости, скорости поворота решетки), полученных при применении указанных гипотез. Весовой коэффициент полагается назначаемой величиной в пределах от 0 (соответствует гипотезе Фойгта) до 1 (гипотезе Рейса). Наряду с взвешенным осреднением полученных по отдельности результатов с использованием гипотез Фойгта и Рейса (линейная модель), предлагается более сложная нелинейная модель осреднения. Последняя основана на минимизации функции , где и соответственно отклонения нормы локальной деформации скорости от средней и локальных напряжений (в зернах) от средних по поликристаллическому агрегату. Минимизация функции r позволяет определить нелинейную зависимость локальных скорости деформаций и напряжений от соответствующих осредненных величин. В статье отсутствует обоснование выбора критерия «оптимального решения».

Е. Кренером было предложено линейное соотношение, связывающее локальные отклонения девиаторов напряжений и пластических деформаций от осредненных , :

,

где – константа материала для n-го зерна. Нетрудно видеть, что полученное соотношение может быть проиллюстрировано структурно-механической моделью, состоящей из параллельно соединенных «цепочек», каждая из которых содержит последовательно соединенные упругий и пластический элементы с различными характеристиками.

В ФТП используются и более сложные подходы к объединению кристаллитов в поликристаллический агрегат. Один из них, называемый «самосогласованной моделью» (или «моделью среднего поля»), основан на решении краевой задачи об одиночном включении (зерне) в матрице, имеющей осредненные («эффективные») характеристики поликристалла. Аналитические решения подобной задачи возможны только для включений канонической формы. Известные самосогласованные модели требуют весьма существенных вычислительных ресурсов, в связи с чем большая часть исследователей предпочитает более простые подходы. С современными самосогласованными моделями можно познакомиться, например, в статье [132]; вариант самосогласованной модели для упруговязкопластической физической теории предложен в работе [154].

Дальнейшим развитием самосогласованных моделей являются так называемые «прямые модели», в которых каждое зерно представляется совокупностью одного или нескольких конечных элементов, для каждого из элементов напрямую используется та или иная физическая теория. Понятно, что в этом случае вопроса о «согласовании» полей перемещений и вектора напряжений не возникает, непрерывность полей обеспечивается автоматически. Однако модели этого класса являются еще более ресурсоемкими, чем самосогласованные.

В связи с тем, что ограничения, накладываемые гипотезой Фойгта, являются слишком жесткими, в начале 80-х годов прошлого века появились работы по модификации модели Тейлора, основанные на «релаксации» («смягчении») геометрических ограничений [175, 177-180]; рассматриваемые модели относятся к классу «промежуточных» (между моделями, основанными на простых гипотезах (Фойгта, Рейсса), и самосогласованными моделями).

В связи с отмеченными выше недостатками моделей, в которых принимается та или иная гипотеза однородности, появились «многозеренные» модели, предельным случаем которых являются прямые модели, основанные на МКЭ. К числу этих моделей относятся следующие [177]: LAMEL, оперирующая с 2-мя зернами, GIA (8 зерен), новая модифицированная модель ALAMEL (advanced LAMEL). В этих моделях поля деформаций теперь не являются однородными. Тем не менее, во всех этих трех моделях осредненные скорости деформаций приравниваются средним предписанным скоростям деформации.

Интересный подход в развитие многозеренных моделей предлагается в [131], названный автором иерархической моделью. Для построения модели используется так называемое «бинарное дерево», представляющее собой совокупность узлов и ветвей, причем из каждого узла исходят две ветви нижележащего иерархического уровня. Высший узел иерархии представляет модель поликристаллического агрегата; элементами низшего уровня («листьями») являются зерна, для элементов нижнего уровня применяется вязкопластическая теория [64].

В работе [97] рассматривается двухуровневая упругопластическая модель. На мезоуровне применяется закон Гука в скоростной релаксационной форме; в качестве меры скорости напряжений использована коротационная «решеточная» производная тензора напряжений Коши. Скорость поворота решетки определяется упругой составляющей тензора вихря. Коэффициенты упрочнения по СС определяются плотностью накопленных дислокаций; приведено эволюционное уравнение для плотности дислокаций, учитывающие генерацию и аннигиляцию дислокаций. Для связи переменных мезо- и макроуровня принимается самосогласованная схема, основанная на решении Эшелби для эллиптического включения.

Представляется необходимым упомянуть о двухуровневом подходе, подробно изложенном в статьях [82, 120, 137, 143, 160], в основу которого положено мультипликативное разложение градиента места мезоуровня и введен новый градиент места, которые авторы называют «тензором мезо–несовместности» и полагают его ответственным за неоднородность упругопластических деформаций в представительном макрообъеме.

В последние годы появились двухуровневые модели, в которых делается попытка учета движения и взаимодействия дискретного множества дислокаций [86 и др.].

Для процессов деформирования поликристаллических тел, в частности – в процессах обработки металлов давлением, характерна существенная неоднородность распределения напряжений и деформаций по области деформирования и, как следствие, значительное различие историй деформирования различных материальных подобластей, их мезо- и микроструктуры.

При использовании многоуровневого подхода исследуемая область на макроуровне заменяется кусочно-однородным с точки зрения историй нагружения аналогом, объем однородных подобластей не должен быть меньше представительного объема (ПО) макроуровня. Для поликристаллических материалов в качестве ПО макроуровня [36, 37, 39,51] обычно принимается конгломерат, включающий не менее 7 структурных элементов мезоуровня по стороне куба (т.е. не менее 343 таких элементов).

В качестве структурных элементов мезоуровня можно рассматривать кристаллиты, представляющие собой модельный однородный материал. Под кристаллитом здесь понимается идеальный кристалл (с той или иной решеткой), обладающий соответствующими анизотропными упругими свойствами и набором систем скольжения: зерно, субзерно, фрагмент зерна. Совокупность кристаллитов, образующих элемент макроуровня, будем называть поликристаллическим агрегатом (ПКА) [1, 36, 37]. Для моделирования взаимодействия элементов ПКА можно ввести дополнительные структурные элементы, описывающие границы зерен. Ориентацию кристаллической решетки кристаллита удобно описывать тремя углами Эйлера или кватернионом, задающими ориентацию кристаллографической системы координат (КСК) элемента относительно лабораторной системы координат (ЛСК), вводимой при постановке макрозадачи.

Поведение представительного объема макроуровня описывается моделью макроуровня, учитывающей геометрические особенности макрозадачи и (или) особенности истории макровоздействий. Для ПКА разрабатывается соответствующая модель мезоуровня, учитывающая распределение ориентаций КСК кристаллитов, особенности границ между кристаллитами (зернами, субзернами, фрагментами), число и расположение в решетке систем скольжения и т.п. В зависимости от поведения материала на макроуровне может понадобиться несколько различных моделей мезоуровня (например, только упругие, упругопластические и/или упруговязкопластические модели).

Рассмотрим более подробно особенности макромодели. Параметрами процесса на макроуровне являются предписанные условия нагружения, которые и определяют эволюцию макронапряжений (Х, t) и/или макродеформаций, задаваемых некоторой мерой деформации М(Х, t), и их скоростей. В качестве определяющих соотношений макроуровня удобно использовать анизотропный закон Гука в скоростной релаксационной форме

,

где Π – тензор модулей упругости, D, – тензор деформации скорости и его пластическая составляющая, индекс r означает коротационную производную на макроуровне. Пластическая составляющая скорости деформации и анизотропные упругие свойства Π в каждый момент деформирования зависят от микроструктуры (а через нее – от истории нагружения), являясь явными внутренними переменными модели макроуровня [38, 51]. Параметры элементов мезоуровня (ориентации КСК, сопротивление сдвигу по системам скольжения (СС), скорости и накопленные сдвиги по СС) выступают в качестве неявных внутренних переменных макроуровня, а в качестве замыкающих уравнений, связывающих макро- и мезоуровень, используются соответствующие гипотезы (Фойгта, Рейса, Кренера и др.).

В силу случайного (по тому или иному закону, определяемому по экспериментальным данным) распределения начальных ориентаций КСК кристаллитов набор значений неявных внутренних переменных (например, ориентаций КСК), фигурирующих в модели ПКА, можно считать выборкой случайных чисел. Тогда правила взаимодействия макро- и мезоуровней сводятся к оценке математических ожиданий соответствующего параметра по имеющейся выборке. Например, скорость пластических деформаций D^p(Х, t) представительного объема Х вычисляется (ориентационным) осреднением выборки скоростей пластических мезодеформаций для момента времени t по всем кристаллитам, содержащемся в данном ПО [1]. При этом предполагается одинаковость хода времени на макро- и мезоуровнях.

Для определения тензора упругих свойств Π на макроуровне можно использовать выборку ориентаций Ф(Х, t) КСК кристаллитов ПКА. Преобразуя компоненты тензора упругих свойств кристаллитов из КСК в ЛСК, получаем выборку упругих свойств в ЛСК. Затем по одной из моделей (Фойгта, Рейса или Хашина–Штрикмана [58]) находятся эффективные упругие свойства ПО в ЛСК, которые без дополнительных преобразований, связанных с поворотами, можно использовать в макрозадаче. По выборке Ф(Х, t) ориентаций КСК кристаллитов ПКА можно построить функцию распределения ориентаций (ФРО), являющейся функцией плотности распределения случайной величины (рис. 8.2).

Макроуровень (представительный объем)

, ,

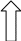
Мезоуровень (зерно, субзерно, фрагмент)

, , O

Рис. 8.2. Схема двухуровневой модели

Как любая методика, двухуровневый подход имеет свои достоинства и недостатки. К достоинствам подхода можно отнести:

• возможность моделирования мезоструктуры поликристалла (распределение ориентаций КСК зерен, их размер и форму);

• моделирование макросвойств, существенно зависящих от мезоструктуры, в частности, анизотропию упругих, пластических и прочностных свойств;

• относительно простой вид определяющих соотношений макроуровня (например, анизотропный закон Гука в релаксационной скоростной форме);

• возможность распараллеливания вычислений;

• применимость к решению существенно нелинейных задач.

Среди недостатков данного подхода можно отметить:

• невозможность получения аналитического решения задачи;

• большое количество неявных внутренних переменных для описания мезоуровня;

• большие запросы по ресурсам памяти и времени ЭВМ;

• высокая трудоемкость разработки программ для ЭВМ.

Многие из отмеченных недостатков носят не принципиальный характер, особенно в свете развития вычислительных технологий. Например, затраты машинного времени можно значительно снизить, используя распараллеливание алгоритма. При этом процедура распараллеливания может быть осуществлена как по отдельным элементам мезоуровня (зернам, фрагментам и т.д.), так и по ПО макроуровня. Для распараллеливания цикла по совокупностям ПКА удобно использовать технологию MPI. Более трудоемким является распараллеливание внутренних по отношению к макроуровню циклов и методов решения СЛАУ макрозадачи. Возможно, что в этом случае больший выигрыш можно получить от использования технологии OpenMP, ориентированной на многоядерность микропроцессоров.