Вопросы к главе 6

1. В чем состоит основное отличие вязкоупругих и вязкопластических моделей?

2. Предложите модификации соотношения для учета влияния температуры.

3. Как изменятся соотношения и при удвоении систем скольжения (то есть при переходе к положительным сдвигам)?

4. Приведите физическое объяснение закона упрочнения ‑.

5. Является ли система уравнений однозначно разрешимой? Каковы критерии ее разрешимости относительно s?

6. Приведите выражение тензора р в для случая одноосного напряженного состояния и одиночного скольжения по СС ГЦК – решетки (ориентация решетки по отношению к оси нагружения выбрать самостоятельно), определите обратный тензор р^-1.

7. Получите самостоятельно выражение .

8. Запишите математическую постановку задачи оптимизации для модели [141] с учетом ограничения типа равенства 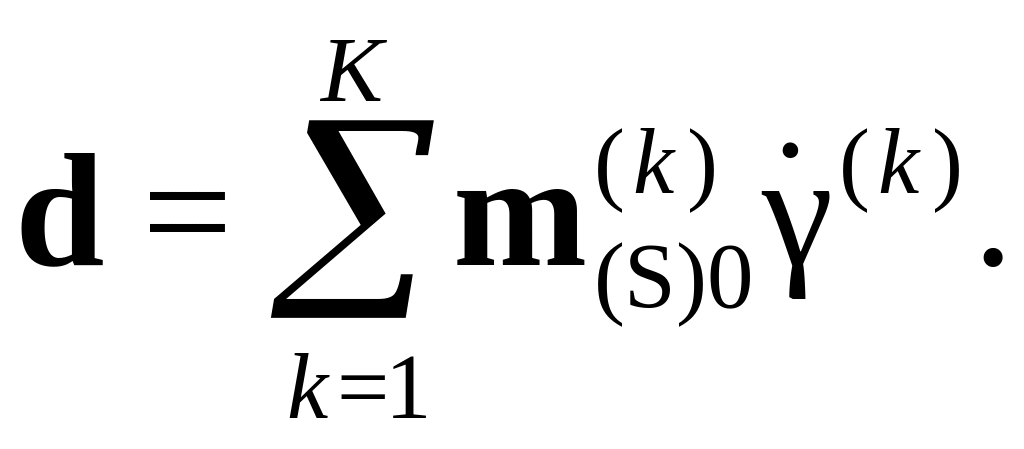_{Что можно сказать о единственности ее решения?}

9. Как описывается ротация кристаллической решетки в рассматриваемых моделях?

Глава 7. Упруговязкопластические модели

7.1 Анализ упруговязкопластических моделей [64, 114]

Обзор работ по физическим теориям пластичности, вязко- и упруговязкопластичности, выполненных до 1985 года, содержится в статье [64]. В ней подробно рассматривается конститутивная модель неупругого деформирования ГЦК поликристаллического агрегата при больших градиентах перемещений. Поскольку данная статья является одной из основополагающих и весьма часто цитируемых работ по ФТП, представляется целесообразным ее детальное рассмотрение. Предлагаемая модель является двухуровневой. Элементом макроуровня является поликристалл, мезоуровня – кристаллит (зерно), способный неупруго деформироваться скольжением краевых дислокаций. Связь низшего масштабного уровня с верхним осуществляется осреднением. Как отмечают авторы, модель пригодна для определения текстуры материала и напряженно-деформированного состояния при различных историях нагружения зерен ГЦК агрегата.

Одной из важных особенностей модели является выбор физически обоснованных законов упрочнения, основанных на экспериментальных данных. В модели описывается деформационное и латентное упрочнение, используются чувствительные к скорости деформирования уравнения состояния и соответствующие параметры материала. Основой предлагаемой модели является конститутивная упругопластическая модель Тейлора-Бишопа-Хилла. В работе предложен ряд модификаций, позволяющий, в частности, решить проблему выбора неединственности активных СС.

Модель мезоуровня

Описание пластического течения, как и многих других моделей ФТП, основывается на работах [164-166]. Некоторые конститутивные соотношения, используемые в данной работе, можно найти в [65, 103]. Зерно деформируется упруговязкопластически, механизмом неупругого деформирования мезоуровня является движение краевых дислокаций. Градиент деформаций (транспонированный градиент места) f записывается с помощью соотношения Ли [121]:

,

где описывает скольжение дислокаций по кристаллографическим СС и связывает отсчетную конфигурацию K₀ с разгруженной K_x, – характеризует упругое деформирование и переводит промежуточную конфигурацию K_x в текущую K_t. Выше использованы обозначения основного (взаимного) лагранжева базиса в отсчетной 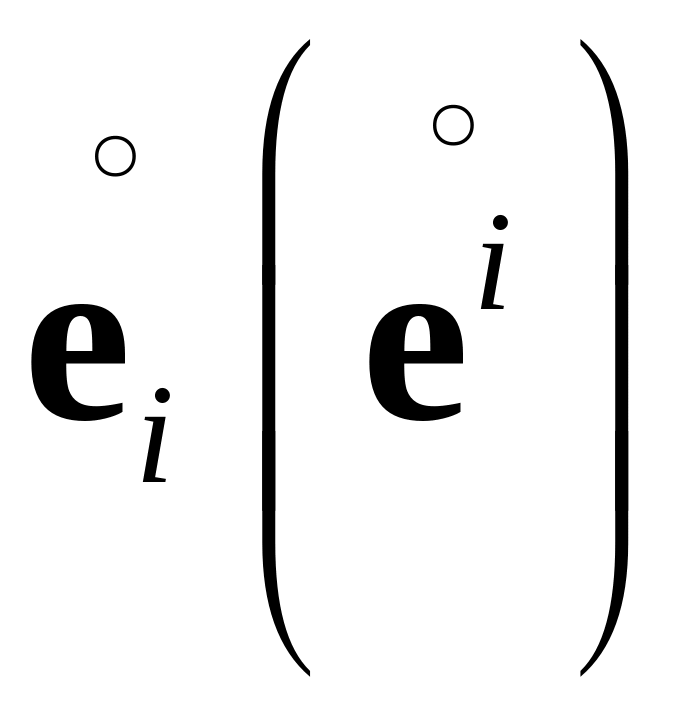, промежуточной 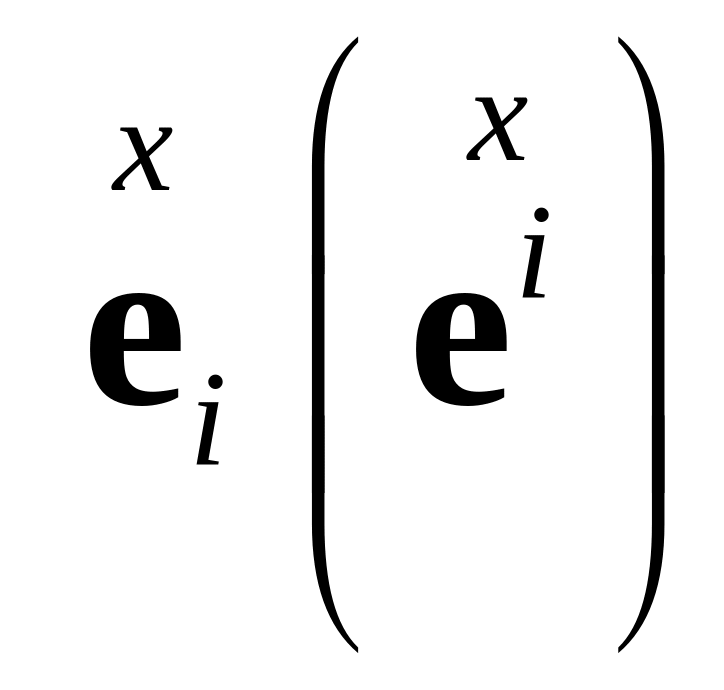и текущей конфигурациях.

Каждая k-ая система скольжения определяется направлением сдвига b^(k) и нормалью плоскости скольжения n^(k). Векторы и являются ортонормированными в недеформированной решетке (в отсчетной и промежуточной конфигурациях), в деформированной решетке (в текущей конфигурации) в анализируемой статье эти направления описываются соотношением:

.

Нетрудно проверить, что в текущей конфигурации векторы также ортогональны. В статье не обсуждается происхождение второго соотношения; вообще говоря, вектор нормали преобразуется при переходе от отсчетной к актуальной конфигурации совершенно аналогично соотношению для вектора направления скольжения: . Вероятно, авторы неявно принимают, что тензор упругих искажений в разложении упругой составляющей градиента места близок к ортогональному тензору (т.е. упругими искажениями пренебрегается); в этом случае , векторы являются единичными.

Используя мультипликативное разложение градиента деформации , можно определить градиент скорости перемещений l:

,

где l^e и lⁱⁿ – упругая и неупругая составляющая градиентов скоростей перемещений в текущей конфигурации. Полагая, что пластическая деформация осуществляется сдвигами по известным СС, используя и разложение lⁱⁿ на симметричную dⁱⁿ и антисимметричную части wⁱⁿ, записывается неупругая составляющая градиентов скоростей перемещения lⁱⁿ:

где – скорость сдвига по k-й CC, dⁱⁿ – пластическая составляющая тензора деформации скорости, wⁱⁿ – пластическая составляющая тензора вихря. Для каждой k-й СС вводятся в рассмотрение симметричные и антисимметричные тензоры:

.

Тогда dⁱⁿ и wⁱⁿ можно записать в виде:

Далее авторы, используя , раскладывают соответствующие составляющие на симметричную и антисимметричные части:

Для дальнейшего рассмотрения кинематики деформирования вводится аналог тензора Коши-Грина, определенный в терминах разгруженной конфигурации . Напомним, что тензор Коши-Грина определяется в отсчетной конфигурации K₀ [31]:

,

где I – единичный тензор; тензор определяется следующим образом:

.

Найдем связь этого тензора с упругой составляющей тензора деформации скорости d^e:

.

Для этого продифференцируем соотношение и полученное выражение слева скалярно умножим на f^e-T, справа – на f^e-1.

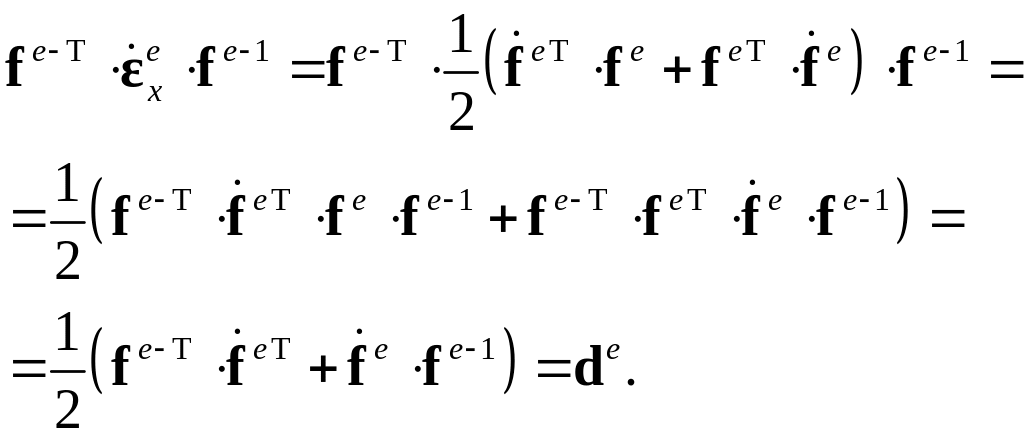
Отсюда следует связь тензоров и d^e:

.

Рассмотрим связь тензора скорости деформаций Коши-Грина и скорости упругого тензора Коши-Грина в разгруженной конфигурации . Продифференцируем соотношение и используем мультипликативное разложение градиента деформаций :

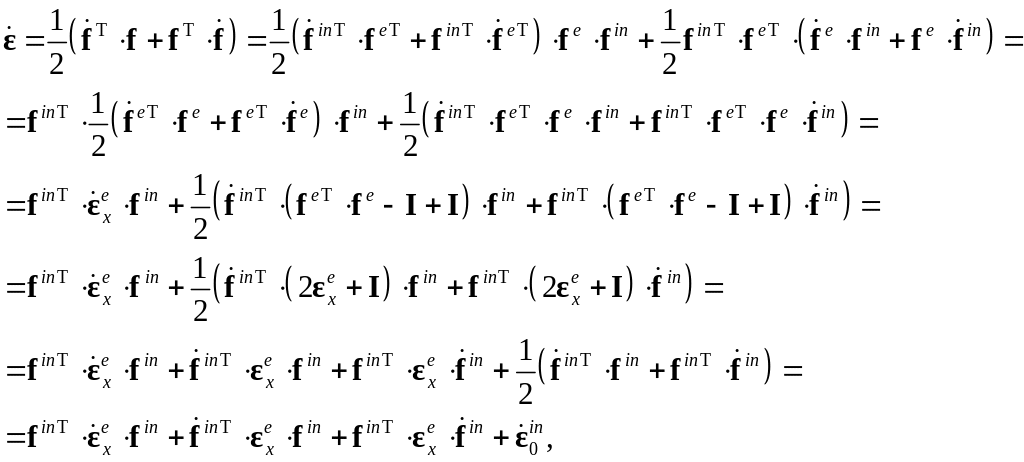
где обозначена скорость неупругого тензора Коши-Грина в отсчетной конфигурации K₀ ( ).

Целью дальнейших выкладок является получение ОС упругопластического тела. Для этого вводится в рассмотрение (упругий) потенциал, устанавливается его физический смысл; далее с помощью последнего определяется вид искомого ОС в скоростной форме.

Напомним, что существует определение упругих материалов, опирающиеся на понятие потенциала. Такие материалы называются упругими по Грину или гиперупругими. Для определения потенциала вводится элементарная работа внешних массовых и поверхностных сил [31]:

,

где δr – виртуальное (возможное) перемещение, δ'A – элементарная работа (δ' говорит о том, что речь идет не о вариации работы, а о работе на виртуальных перемещениях). Используя соотношение Коши, теорему Гаусса-Остроградского и уравнение движения сплошной среды, можно показать, что в случае квазистатического нагружения:

,

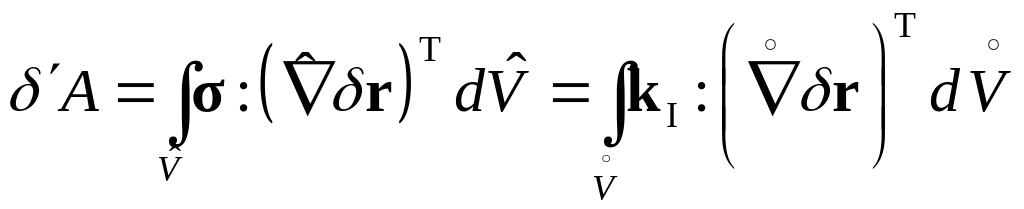где – I-й тензор Пиолы-Кирхгоффа, σ – тензор напряжений Коши. Вводя обозначение 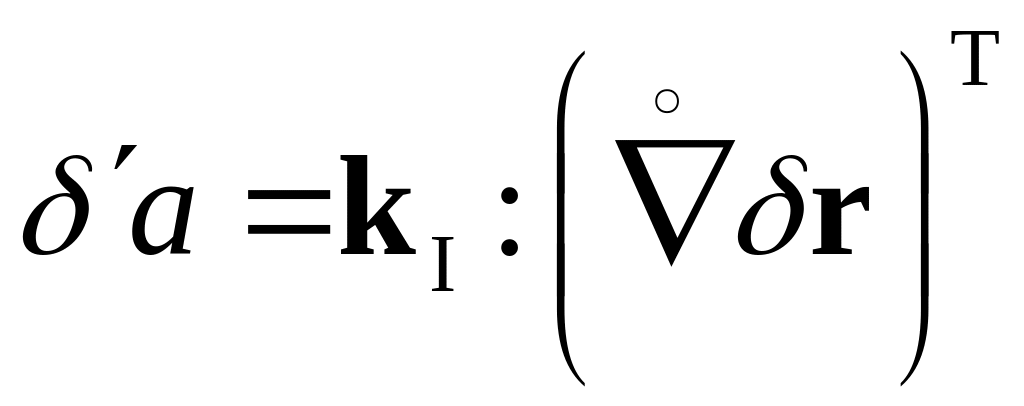для элементарной работы на единицу объема в K₀, можно записать:

.

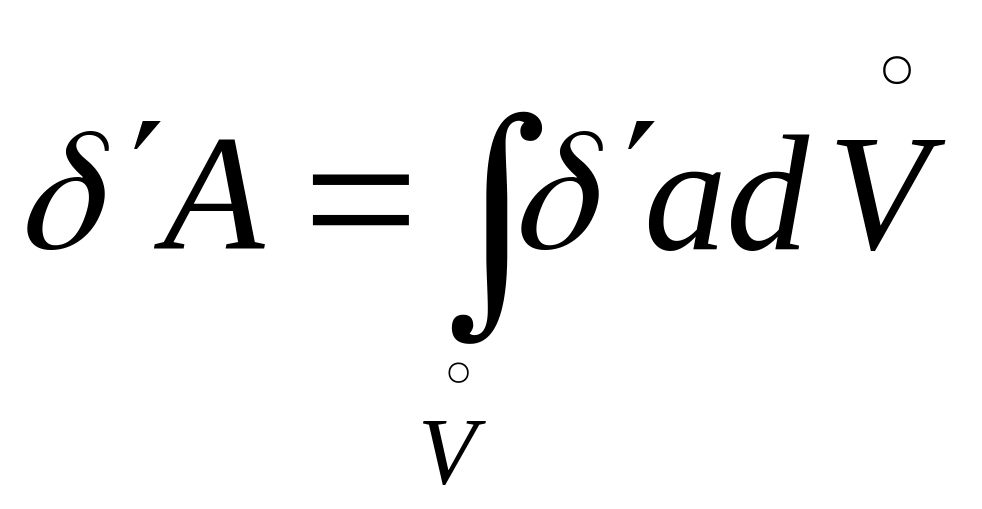Введенное определение дополняется требованием существования потенциала  – функции некоторой меры деформации, удовлетворяющей условию:

,

– вариация потенциала. Величина  характеризует запасенную в результате деформирования упругую энергию на единицу объема в K₀ [31]. Потенциальная энергия тела определяется интегрированием  по объему тела.

Напомним определение производной F_t скалярнозначной функции F тензорного аргумента A, который в свою очередь зависит от скалярной переменной t:

.

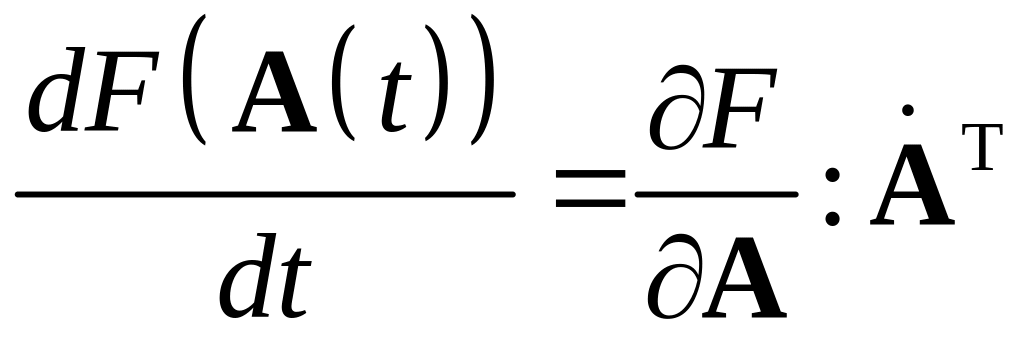В дальнейших выкладках понадобиться цепное правило для тензоров второго ранга, которое определяется соотношениями:

(А·B) :C=(А·B·C):I=(B·C·А):I=(B·C):А= (C·А):B,

В работе принимается, что упругость кристалла не зависит от скольжения и определяется удельной энергией упругой деформации . Скорость работы напряжений в единице объема зерна определяется соотношением:

где k – взвешенный тензор Кирхгоффа, равный тензору Коши σ, умноженному на det(f), – сдвиговые напряжения по k-й СС. Преобразуем , используя тензор скорости упругих деформаций Коши-Грина, определенный в разгруженной конфигурации [103], соотношения ₁ и :

.

Используя выражение для производной и симметричность тензора , найдем скорость изменения величины :

,

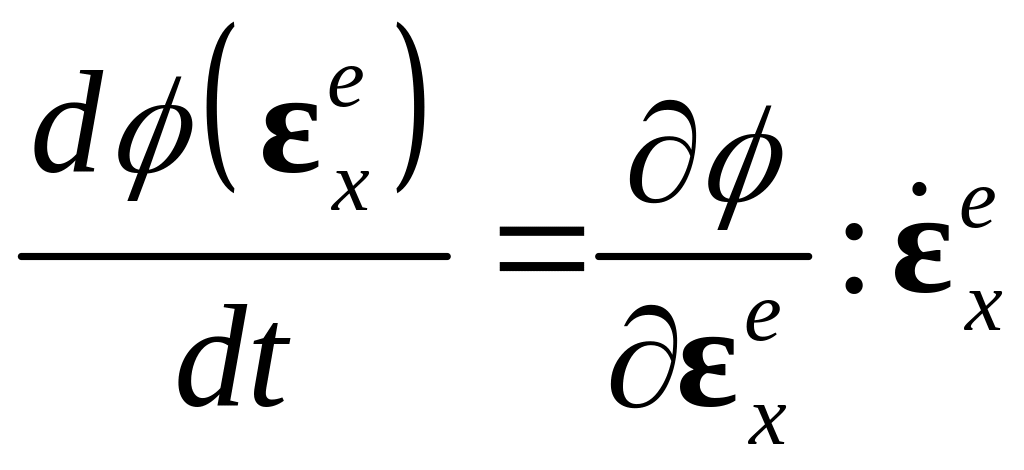Поскольку потенциал  характеризует запасенную упругую энергию на единицу объема, то полная производная по времени – скорость этой величины (сравнить с первым слагаемым правой части или ). Сопоставляя первое слагаемое правой части и , получаем:

,

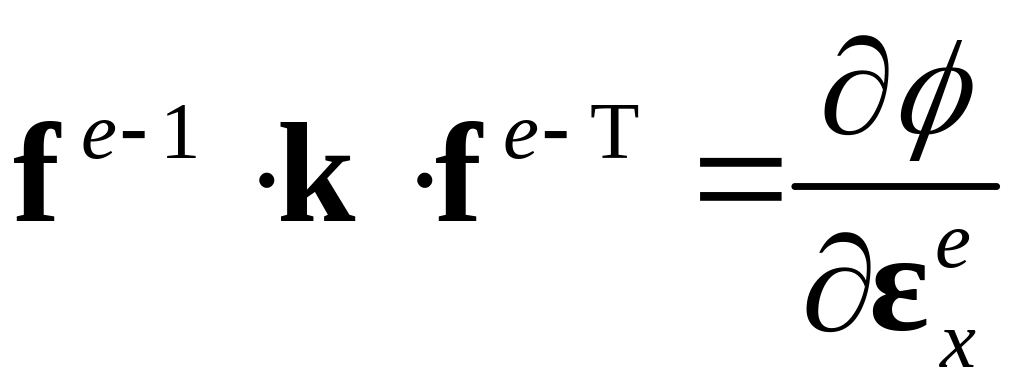или

.

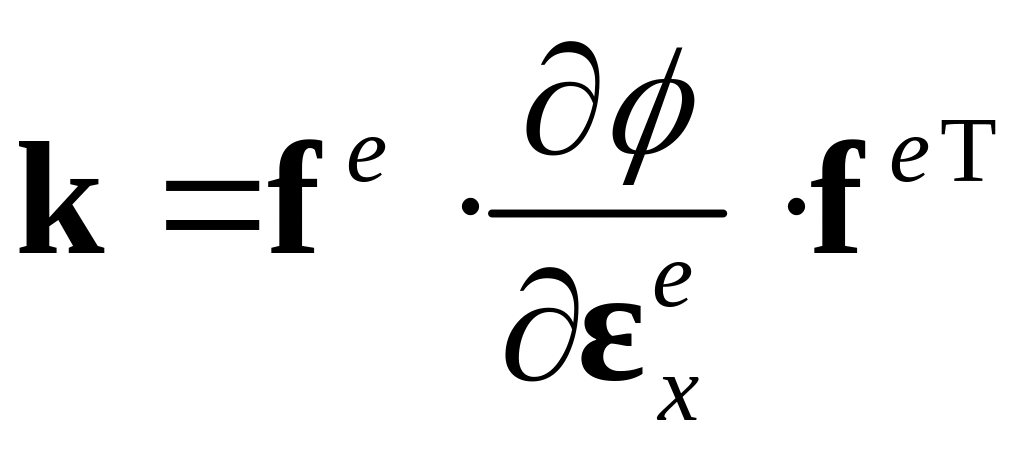Следует отметить, что в физических уравнениях упругого типа напряжения связаны с упругими деформациями, тогда как в соотношениях неупругого типа (вязких, пластических, вязкопластических и т.д.) фигурируют соответствующие составляющие тензора деформации скорости, выражаемые через напряжения. При этом соотношения для каждой из составляющих мер деформации или скорости деформации записываются независимо. С другой стороны, кинематические соотношения связывают деформации или скорости деформации с полями соответственно (полных) перемещений или скоростей перемещений, которые не могут быть разделены на составляющие. Для объединения составляющих мер деформации или скорости деформации в «полные» применяются или мультипликативное, или аддитивное разложения мер, для чего требуется приведение мер к одному типу – либо к деформациям, либо к скоростям деформации. В рассматриваемой работе использовано аддитивное разложение тензора деформации скорости; в связи с вышесказанным в законе упругости требуется переход к скоростям деформаций и напряжений. Для этого продифференцируем соотношение :

.

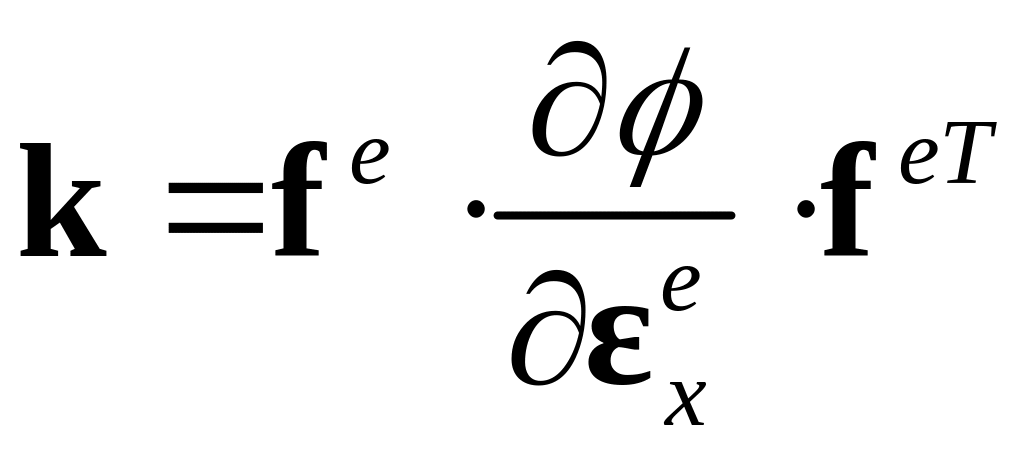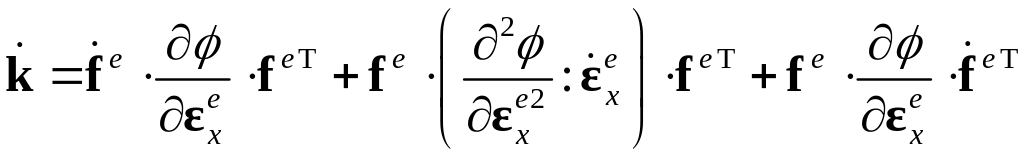Перепишем соотношение в виде:

.

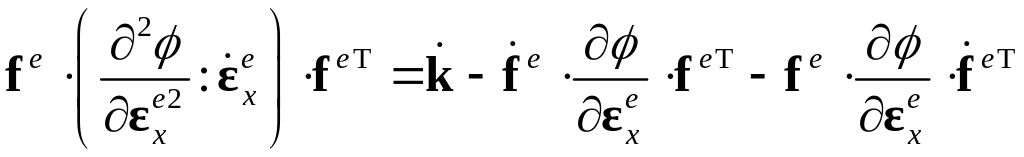Обозначим тензор четвертого ранга , определенный в разгруженной конфигурации K_x, как 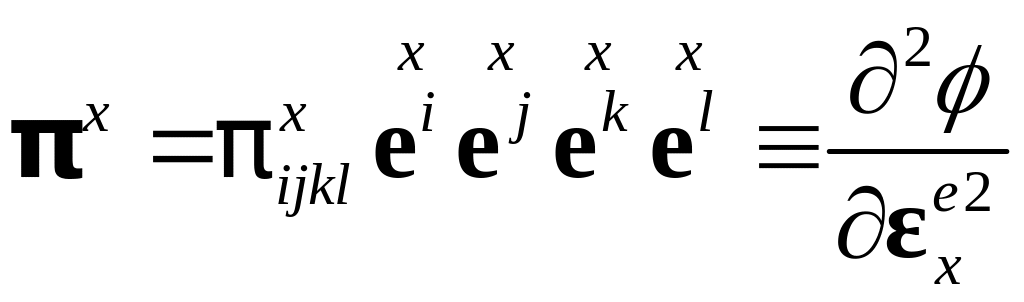. Напомним, что когда говорится «тензор, определенный в терминах (или в базисе) той или иной конфигурации», это означает, что компоненты тензора в соответствующем базисе имеют ясно выраженный физический (геометрический, энергетический) смысл. Разумеется, тензор в силу своих свойств можно преобразовать в любой другой базис, однако при этом, как правило, теряется физический смысл его компонент. Поскольку упругие деформации малы, производную можно определить в нуле, используя разложение в ряд Тейлора и ограничиваясь вторым порядком. Заметим, что для выявления симметрийных свойств удобно воспользоваться кристаллографической системой координат.

Левую часть соотношения в компонентах можно писать следующим образом (вывод предоставляется читателю):

Отметим, что справедливо равенство:

,

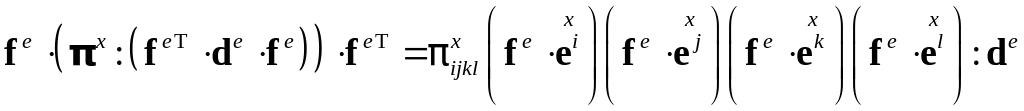в чем можно убедиться, записав правую часть в компонентах. Введем в рассмотрение математический объект с:

.

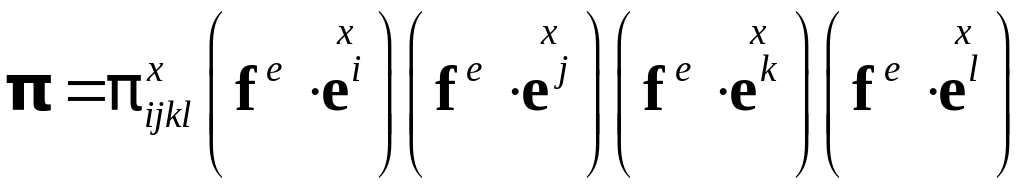Возникает вопрос о природе введенного объекта – является ли он тензором? Заметим, что π образован из компонент тензора 4-го ранга π^х в базисе разгруженной конфигурации и полиадного базиса в актуальной конфигурации. Напомним, что тензор – величина инвариантная по отношению к выбору системы координат, в то время как его компоненты изменяются при переходе к другому базису (по вполне определенному закону [50]). Согласно этому закону при разложении векторов «старого» базиса по векторам «нового» базиса (и наоборот)

,

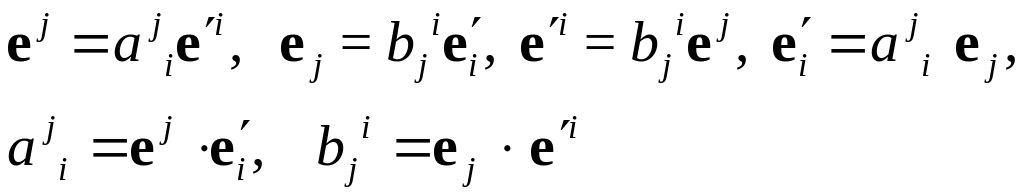компоненты, например, тензора четвертого ранга преобразуются следующим образом:

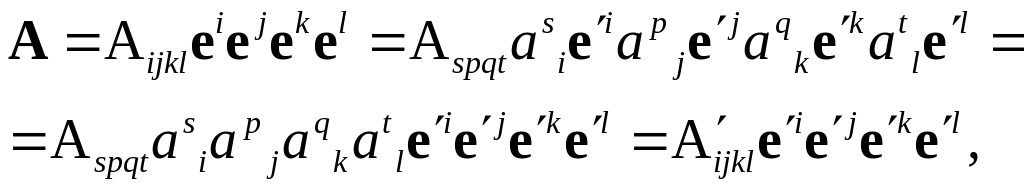
то есть:

.

Аналогичным образом, взяв за исходную запись тензора А в «новом» базисе, можно показать, что

Нетрудно показать, что контравариантные компоненты тензора преобразуются с помощью матрицы , при этом матрицы и взаимообратны, = , ( – дельта Кронекера). Сопоставляя ₁ и , ₃ и , легко обнаружить, что компоненты и базисные векторы преобразуются с помощью взаимообратных матриц, что и предопределяет неизменность тензоров при заменах систем координат.

Для решения поставленного выше вопроса (о природе введенного объекта с) расширим обычную алгебру тензорного исчисления новой операцией – позиционного умножения. Рассмотрим ее на примере двух тензоров М (ранга т) и N (ранга п). Позиционным (p, q) произведением (1≤ p ≤ т, 1≤ q ≤ п) тензоров М и N будем называть тензор L ранга (т+п–2), определяемый соотношением:

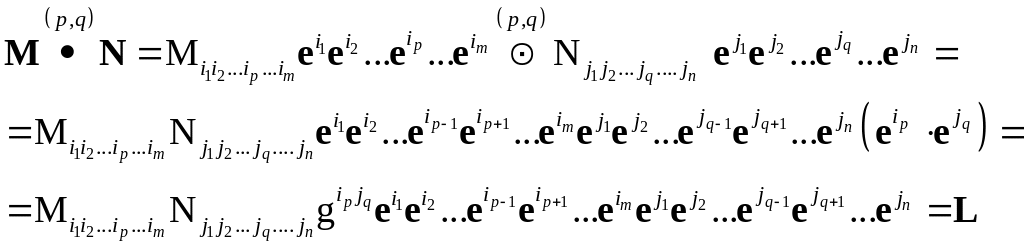
где (p, q) – номера перемножаемых базисных векторов и тензоров М и N, g^ij – (контравариантные) компоненты метрического тензора. То, что L представляет собой действительно тензор, можно показать аналогично приведенному выше примеру, доказательство предоставляется читателю.

С использованием введенной операции позиционного умножения выражение можно записать в виде:

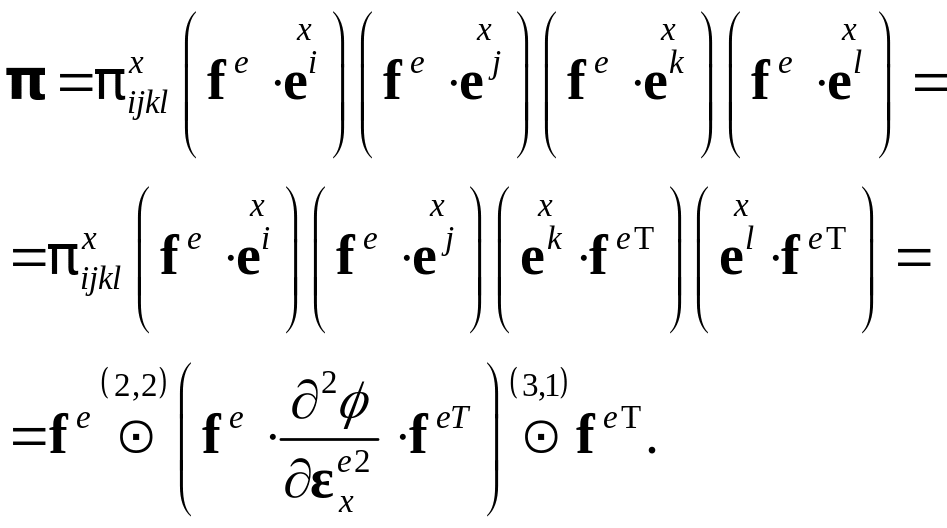
Таким образом, π действительно является тензором (4-го ранга), однако отличным от тензора π^х. При этом из приведенных выводов вытекает, что левую часть соотношения можно представить в виде: . Следует отметить, что в цитируемой работе приводится несколько иной вид тензора π:

.

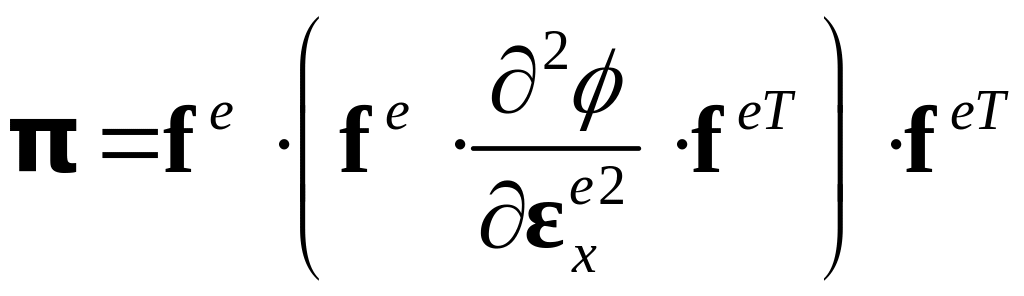К сожалению, авторам не удалось доказать правомочность такого перехода, вероятно, он не верен.

Преобразуем правую часть соотношения :

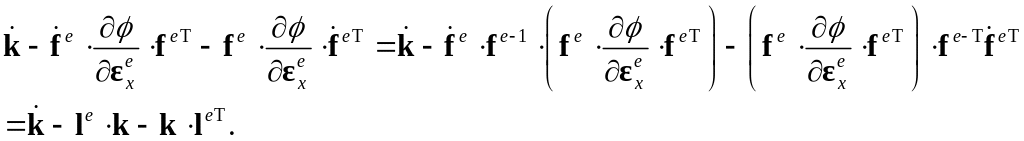
Тогда соотношение может быть приведено к виду:

.

Подставим разложение упругой составляющей градиентов скоростей перемещения l^e на симметричную d^e и антисимметричную части w^e в последнее соотношение:

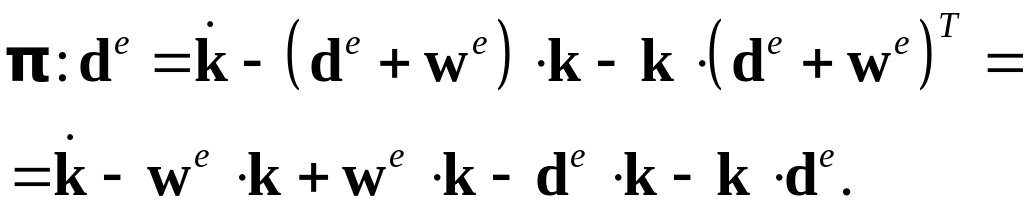
В учтено, что . Группируя слагаемые в соотношении , перейдем к виду:

Проанализируем члены в левой и правой частях соотношения. В левой части учтем, что для металлов, подвергаемых упругопластическому деформированию, компоненты напряжений на несколько порядков меньше упругих модулей (случай гидростатического нагружения при сверхвысоких давлениях из рассмотрения исключается), в силу чего 2-м и 3-м слагаемыми в левой части можно пренебречь. В правой части, учитывая, что рассматривается геометрически нелинейная проблема при произвольных градиентах скоростей перемещений (а следовательно – произвольных ), 2-м и 3-м членами в общем случае пренебречь не представляется возможным. Соотношение тогда примет вид:

Используя , преобразуем к следующему виду:

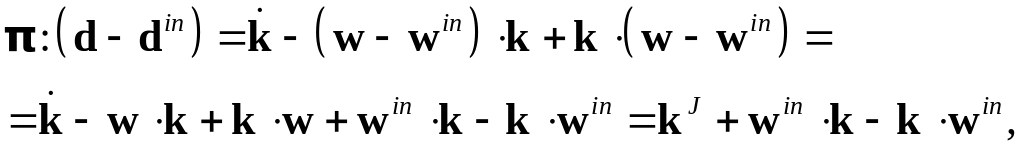
или

где введено обозначение производной Яуманна взвешенного тензора напряжений Кирхгоффа . Применяя , перепишем соотношение в виде:

Далее авторы статьи конкретизируют выражения для скоростей сдвигов . Отмечается, что зависят, в первую очередь, от напряженного состояния через сдвиговые напряжения на каждой k-й СС. Для описания скорости сдвига используется степенной закон Хатчинсона [105].

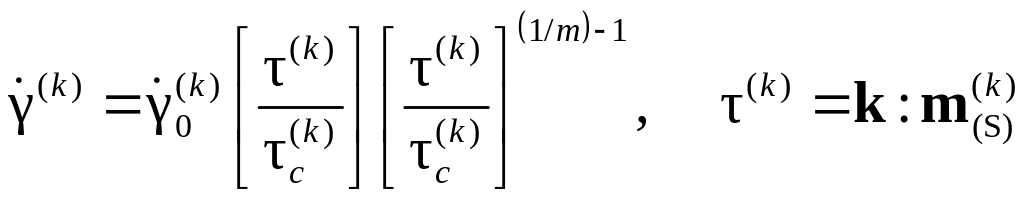
где – скорость сдвига при сдвиговых напряжениях τ^(k), равных критическим , которые полагаются одинаковыми для всех СС, m – параметр скоростной чувствительности материала. Скорости сдвигов однозначно определяются соотношением и в теориях вязкоупругого типа отличны от нуля при любых сдвиговых напряжениях на СС, не равных нулю; в упруговязкопластических моделях скорости сдвигов полагаются равными нулю при τ^(k) . При этом не возникает вопроса о выборе активных СС и их числе, все скорости сдвигов определяются независимо по сдвиговым напряжениям.

В цитируемой работе приводится часто используемый простейший закон изотропного упрочнения, согласно которому упрочнение (изменение ) принимается одинаковым для всех СС и зависящим от накопленного суммарного сдвига γ:

.

Рассматривается также более сложная форма закона упрочнения. Изменение критических напряжений определяется соотношением:

h_αβ – функция накопленного сдвига γ ₂. В недеформированной конфигурации каждое принимается равным τ₀. Соотношение для h_αβ принято аналогичным предложенному в работе [106]:

,

безразмерный параметр q определяет отношение величины латентного упрочнения к деформационному, h (размерность Па) – параметр, характеризующий активное (деформационное) упрочнение, δ_αβ – символ Кронекера. Принятый в работе закон латентного упрочнения подтвержден экспериментальными данными [150]. Для компланарных систем отношение латентного упрочения к деформационному упрочнению близко к 1, для некомпланарных – изменяется в диапазоне от 1.0 до 1.4. При вычислениях для компланарных СС параметр q=1, для некомпланарных q=1.4.

Модель поликристалла

В цитируемой работе авторы рассматривают агрегат, состоящий из большого числа зерен. Отклик каждого зерна описывается ОС . Через S_ext обозначается внешняя поверхность поликристалла, ограничивающая представительный макрообъем V.

Рассматривается квазистатическое нагружение, массовыми силами пренебрегается, граничные условия в перемещениях принимаются такими, что деформации являются однородными в образце. Переход от мезоуровня к макроуровню представляет собой осреднение по объему [102]. В предлагаемой модели условия совместность и равновесие выполняется в каждом зерне, но равновесие может быть нарушено между зернами.

Далее в рассмотрение вводится первый тензор Пиола–Кирхгоффа k_I, связанный с взвешенным тензором Кирхгоффа соотношением:

Сила dP, действующая в произвольный момент времени t на единичную площадку в K_t, но отнесенная к единице площади в K₀, определяется уравнением:

где N и dS задают направление и площадь материальной площадки в отсчетной конфигурации K₀.

Через F обозначается деформационный градиент макроуровня, который согласно принимаемой гипотезе Фойгта однороден в рамках представительного объема. Принимается гипотеза, что первый тензор Пиола–Кирхгоффа k_I удовлетворяет условию равновесия в пределах каждого зерна (но не между ними). Записывается работа внешних сил по объему агрегата, которая представима суммой интегралов по подобъемам, далее используется теорема Гаусса–Остроградского:

где – объем g-го зерна, ∆t – разница усилий между зернами по границе зерна; – межзереннная граница в агрегате. Заметим, что первый член правой части является суммой по всем межзеренным границам в агрегате.

Условия однородных перемещений на внешней границе S_ext можно представить в виде . Тогда последнее выражение можно записать следующим образом:

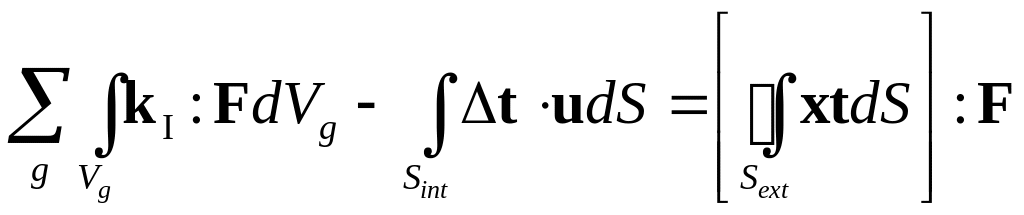
Далее авторами работы принимается существенное допущение, лежащие в основе процедуры осреднения, которое состоит в том, что второе слагаемое левой части пренебрежимо мало по отношению к остальным слагаемым. Отметим сомнительность этой гипотезы и отсутствие каких-либо попыток ее обоснования со стороны авторов цитируемой работы. Тогда можно записать:

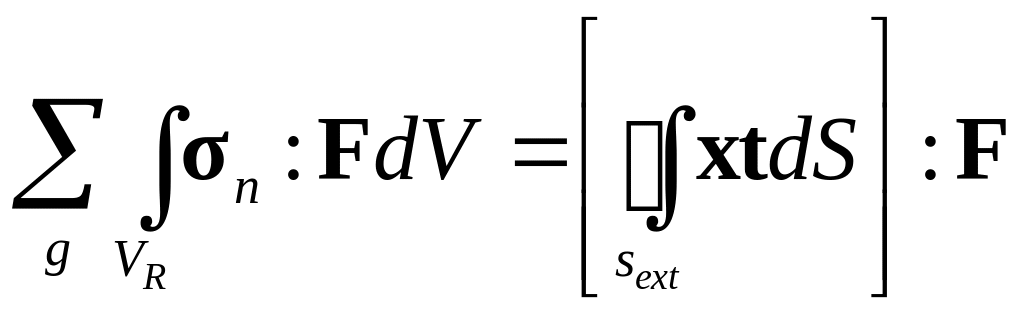
Полагая F однородным по всему объему поликристаллического агрегата, приводится к виду:

.

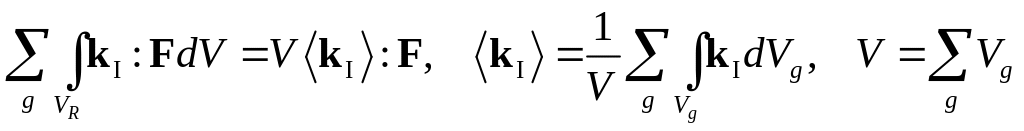Данная модель использовалась для вычисления напряженно-деформированного состояния упрочняющегося материала ГЦК–поликристалла. Авторы работы отмечают, что предлагаемая модель пригодна для описания формирования текстуры материала. Проанализировано влияние упрочнения на текстуробразование и рассмотрено влияние параметра скоростной чувствительности m на текстурообразование. Хорошее согласование с экспериментами показывают результаты расчетов при принятой низкой скоростной чувствительности (использовано m=0.005); уменьшение этого параметра приводит к более четко выраженной текстуре, что не так хорошо согласуется с экспериментальными данными. В работе представлены обратные полюсные фигуры при различных схемах нагружения (сжатие, растяжение) и на различных стадиях деформирования.

Подробно рассмотрена процедура численного решения. Исследовалось поведение поликристаллической меди (закон распределения начальной ориентации зерен – равномерный) при растяжении и сжатии в условиях осевой симметрии и плоско-деформированного состояния. Использовались смешанные граничные условия, объемными силами пренебрегалось, принята гипотеза Фойгта; в качестве процедуры определения осредненных напряжений для представительного объема поликристалла принято осреднение по объему. Приведены результаты расчета развития текстуры, отмечается существенное влияние на её эволюцию параметра латентного упрочнения. Представлены расчетные кривые «интенсивность напряжений – интенсивность деформаций» для различных значений параметра латентного упрочнения. Отмечается достаточно быстрый (при ) выход упрочнения на уровень насыщения; дальнейший рост интенсивности напряжений при больших деформациях ( ) связывается с формированием текстуры («геометрическое упрочнение»).

Для случая комбинированного нагружения (растяжение – сжатие с одновременным сдвигом) при различных предварительных деформациях растяжения и сжатия построены условные «поверхности текучести» с различным допуском на неупругие деформации. Из полученных расчетных кривых видно, что предлагаемая модель качественно описывает образование «носика» на поверхности текучести в направлении нагружения, уплощение тыльной части поверхности, эффект Баушингера.

К работе [64] вплотную примыкает работа [114]. В работе рассматривается упруговязкопластическая модель неупругого деформирования поликристалла. В отличие от более ранней работы [64] в [114] учитывается термоактивируемое движение дислокаций; законы упрочения основаны на модели «механического порогового напряжения» (MTS – mechanical threshold stress), предложенной Фоллансби и Куксом [93]. Отмечается, что модель способна описывать отклик материала на макроуровне и эволюцию кристаллографической текстуры. Численное моделирование проводилось для поликристалла тантала (ОЦК ‑ решетка) коммерческой чистоты при деформациях около 60%; скорость нагружения варьировалась в широких пределах от квазистатического нагружения до скорости деформирования 30 с^-1; изменения температуры были в диапазоне от 200 до 525 ºС.

В цитируемой работе также используется мультипликативное разложение деформационного градиента (транспонированного градиента места):

где f^e – упругая составляющая деформационного градиента, fⁱⁿ – неупругая составляющая, описывающая эффективное движение дислокаций по СС. В силу изохоричности неупругих деформаций det(fⁱⁿ)=1, det(f^e)>0.

Вводятся в рассмотрение следующие меры напряженного состояния: первый тензор Пиола–Кирхгоффа , второй тензор Пиола–Кирхгоффа в разгруженной конфигурации K_x:

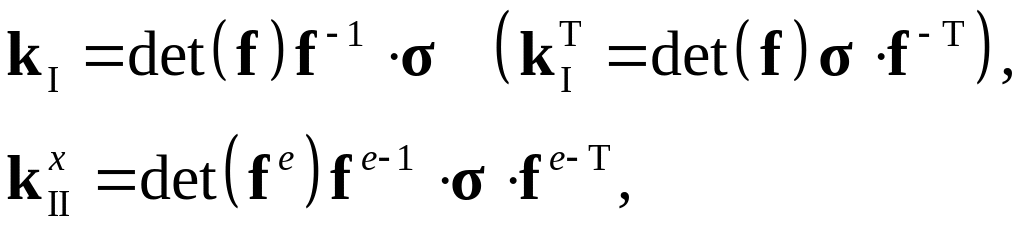
где σ – тензор напряжений Коши. Определяется тензор упругих деформаций Коши-Грина в разгруженной конфигурации K_x:

.

Отмечается, что неупругий градиент скорости перемещений полностью определяется движением краевых дислокаций по известным СС и представим в виде:

,

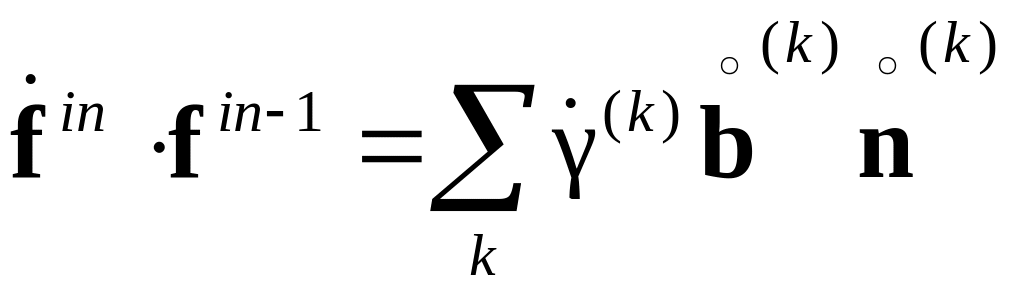где – единичные векторы в направлении вектора Бюргерса и нормали k-й СС. Авторы цитируемой работы отмечают, что выражения для скоростей сдвига по СС можно описать степенными соотношениями вида [105]:

,

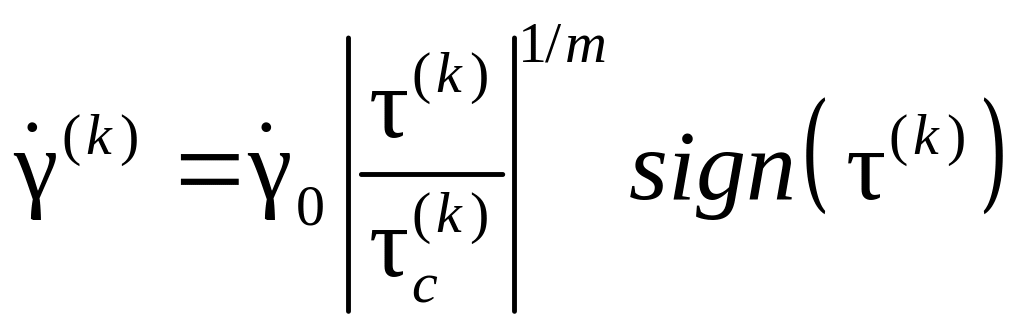где – сдвиговые касательные напряжения, – критические напряжения сдвига, – скорость сдвига при сдвиговых напряжениях , равных критическим, m – параметр, характеризующий скоростную чувствительность материала (модель называется независимой от скорости, если ). Однако, такое упрощенное описание скоростей сдвигов СС пригодно для вязкопластических материалов только в узком диапазоне скоростей деформаций и температур, но не пригодно для описания динамических нагружений, в связи с чем предлагается модифицировать это соотношение, опираясь на уравнение Орована.

Скорость сдвига k-й CC может определяться соотношением Орована [147], которое отражает физическую картину движения дислокаций при плотности подвижных дислокаций с модулем вектора Бюргерса b:

,

где – величина средней скорости движения дислокаций по k-й СС, которая в общем виде является функцией сдвиговых напряжения , критических напряжений и абсолютной температуры θ:

,

Отмечается, что критические напряжения сдвига характеризуют силу взаимодействия подвижных дислокаций и препятствий, плотность и взаиморасположение этих препятствий:

.

Для средней скорости движения дислокаций по k-й СС при сдвиговых напряжениях принимается:

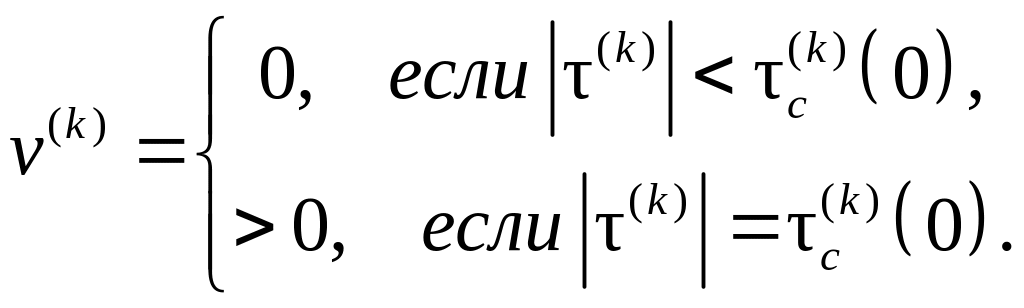
Здесь – критические напряжения сдвига при абсолютной температуре, равной нулевой, при этом полагается, что превышение сдвиговыми напряжениями на СС значения невозможно.

Сопротивление сдвигу при абсолютном нуле температуры называется «механическим пороговым напряжением» (MTS – mechanical threshold stress) [93, 112]. Авторы работы отмечают, что в реальных материалах в силу флуктуаций микроструктуры скорость дислокаций не будет изменяться скачком, как в соотношении , однако «пороговый» характер будет проявляться.

При температуре θ>0 неупругое деформирование может протекать посредством нескольких физических механизмов. Во-первых, поскольку основным механизмом, определяющим величину критического напряжения , является упругое взаимодействие атомов, то повышение температуры, которое сопровождается уменьшением модулей упругости, приводит к снижению величины , поэтому при θ>0 . Во-вторых, что, вероятно, более важно, с повышением температуры локальные близкодействующие барьеры движению дислокаций (с характерным размером менее 10 атомных диаметров) могут быть преодолены при достаточно низких напряжениях сдвига за счет тепловых флуктуаций.

Таким образом, по утверждению авторов, можно разделить барьеры для движения дислокаций на два типа: 1) которые могут быть преодолены с помощью термической флуктуаций, и 2) которые непреодолимы за счет термических флуктуаций. Соответственно критическое напряжение сдвига предлагается разложить на две составляющие – термическую и атермическую:

,

где – описывает вклад в упрочнение барьеров 1-го типа, – барьерами 2-го типа. Типичные примерами атермических барьеров являются группы дислокаций, большие некогерентные включения. Напряжениями Пайерлса, примесные атомы, лесовые дислокации – барьеры 1-го типа. Следует заметить, что в цитируемой работе не обсуждается вопрос о приемлемости гипотезы об аддитивности вкладов от двух указанных типов барьеров. Также вызывает вопросы явная зависимость атермической составляющей от температуры, возможно, авторы имели в виду косвенное влияние на критические атермические напряжения упругих и прочностных свойств дальнодействующих барьеров.

В рассмотрение вводятся эффективные сдвиговые напряжения τ_eff, определяемые соотношением:

.

Отмечается, что данные напряжения характеризуют термическую составляющую напряжений и применимы для описания ОЦК и ГПУ кристаллов (напряжения Пайерлса возрастают с уменьшением температуры). Тогда соотношение может быть записано следующим образом:

Основываясь на ранее опубликованной монографии A.S. Krausz и H.E.Eyring (1975), вводится свободная энтальпия активации (или свободная энергия Гиббса) , которая определяет величину энергии, необходимой для преодоления барьера и реализации приращения сдвига. Величина 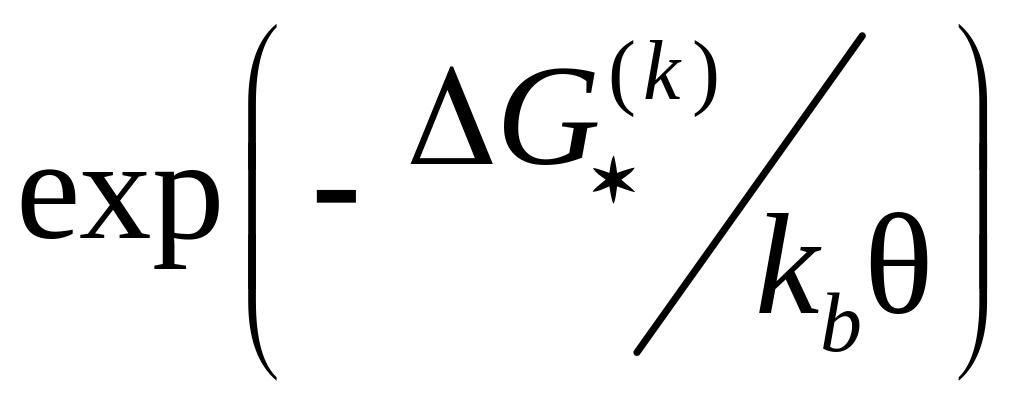(k_b – константа Больцмана) является вероятностью того, что термическая флуктуация энергии, равная (или выше) требуемой величины для осуществления приращения сдвига, имеет место в материале при температуре θ>0. Скорость, с которой дислокации преодолевают препятствия, определяется выражением:

,

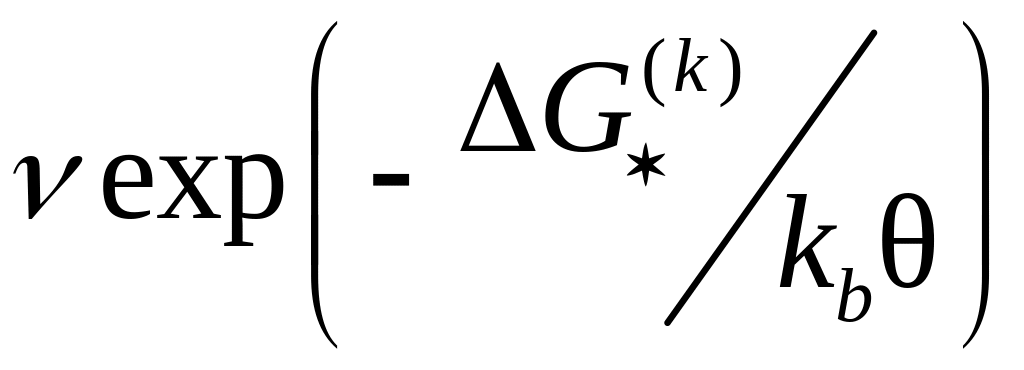где – характерная частота (порядка 10¹² c^-1). Обозначая l^(k) среднюю длину пробега дислокации, записывается средняя скорость движения дислокаций:

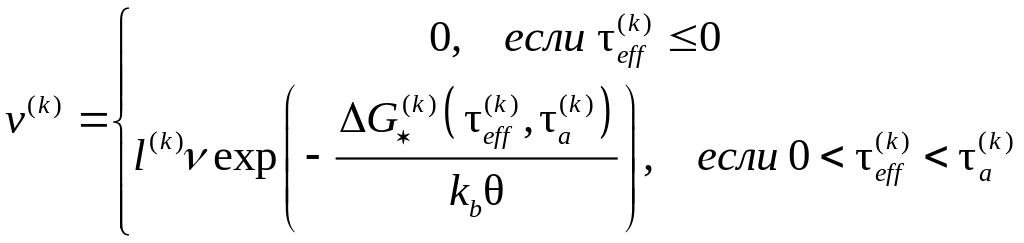
Используя и соотношение Орована, скорости сдвигов могут быть преобразованы к виду:

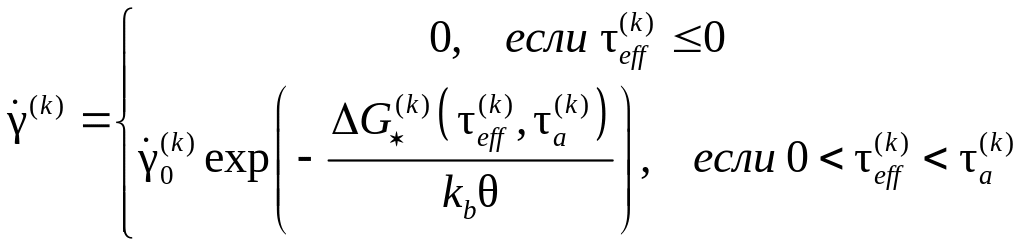
где . Полагается, что для упрощения модели множитель можно принять одинаковым на всех СС, обозначив его как , величина имеет порядок . Следует заметить, что в общем случае является функцией приложенных напряжений и температуры [112], однако в цитируемой работе эта зависимость не учитывается.

В работе [112] конкретизируется выражение для свободной энтальпии :

,

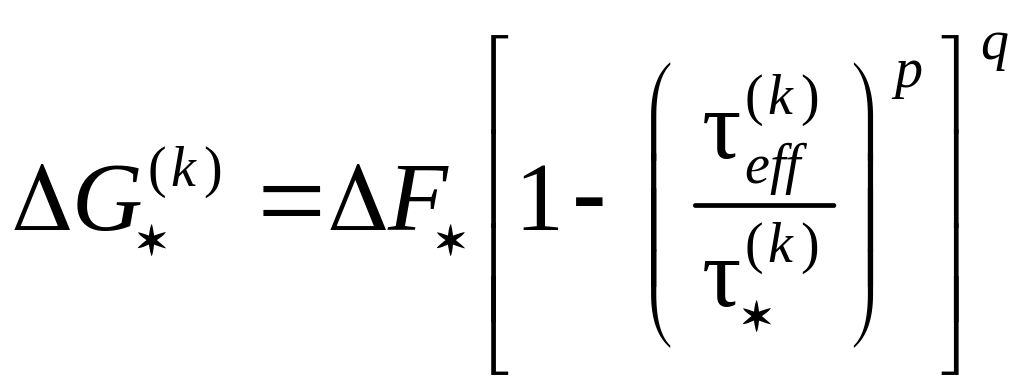где – свободная энергия активации, требуемая для преодоления барьеров скольжением без помощи приложенных сдвиговых напряжений, которая в анализируемой работе полагается одинаковой для всех СС и не изменяющейся в случае, если вид препятствий не меняется. Энергия активации лежит в диапазоне:

,

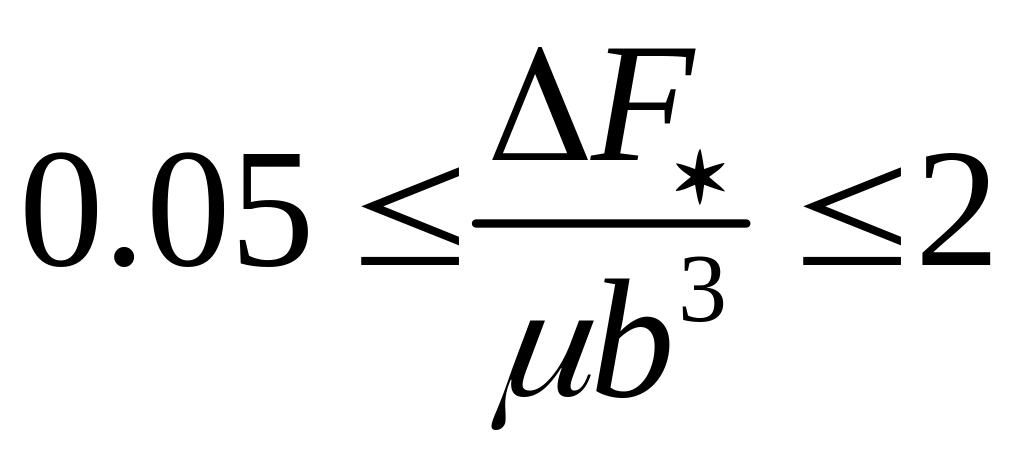где μ – модуль сдвига, b – модуль вектора Бюргерса. Параметры p и q могут принимать значения: .

При неупругом деформировании кристаллита предлагается использовать соотношение:

,

где 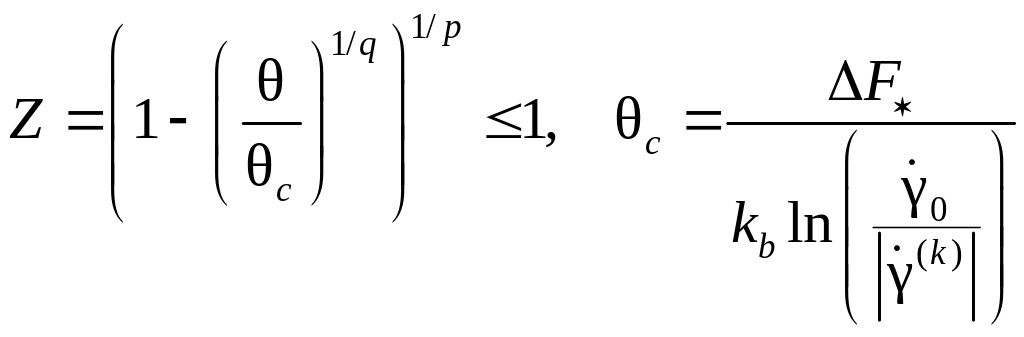. При θ=0 параметр Z=1, при получаем Z=0. Таким образом, делается вывод, что температура превышающая значение , является достаточной для преодоления дислокацией препятствия посредством термической флуктуации (без приложенных сдвиговых напряжений). Отметим, что соотношение представляется несколько не понятным, поскольку действующие касательное напряжение определяется параметрами материала; вероятно, подразумевалось критическое напряжение сдвига.

Законы упрочнения

Сдвиговые напряжения k-й СС определяются согласно соотношению:

Последнее соотношение можно преобразовать к более привычному виду, часто используемому в законе Шмида:

где – взвешенный тензор Кирхгоффа (учтено, что ). Принимается, что упругая составляющая тензора искажений близка к единичному тензору, а сам можно считать ортогональным тензором: ; , – ортонормированные векторы k-й СС в актуальной конфигурации.

В работе используется закон упрочнения стандартного типа:

,

где – скорость сдвига по β-й CC, h^αβ – матрица модулей упрочнения (описывает деформационное и латентное упрочнение). Использование модуля скоростей сдвигов отражает то обстоятельство, что упрочнение незначительно зависит от направления сдвига. Каждый элемент матрицы h^αβ зависит от истории деформирования.

Поскольку в работе используется разложение на атермическую и термическую составляющую , то ключевым моментом является определение эволюционных соотношения для внутренних переменных . По мнению авторов, для ОЦК–кристаллов, в которых характеризует напряжения Пайерлса, можно принять:

,

и

Следует заметить, что вывод о том, что термические составляющие критических напряжений могут быть постоянными, вызывает некоторые сомнения, так как к этой составляющей авторы также относят дислокации леса, конфигурация и плотность которых не могут считаться постоянными.

Матрица модулей упрочнения принимается в виде [150]:

,

h^β – параметр деформационного упрочнения, q₁ – параметр латентного упрочнения. Отмечается, что q₁ не обязательно должен быть постоянным и может, как и h^β, зависеть от истории нагружения.

Основной целью данной работы является формулировка конститутивной модели для описания неупругого деформирования поликристаллов при сложном нагружения. В связи с этим авторы предлагают усложнить эволюционное соотношение для параметра h^β [76]:

.

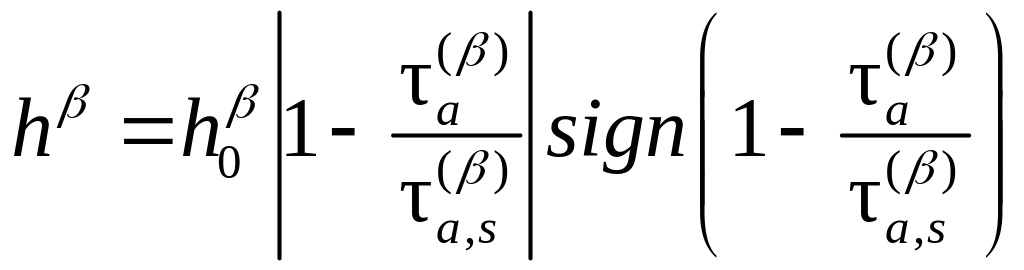где параметры модели зависят от скорости деформирования и температуры: и – напряжение насыщения для .

В качестве определяющего соотношения для монокристалла в цитируемой работе выступают термоупругий закон Гука, записанный в разгруженной конфигурации K_x:

где π – тензор 4-го ранга упругих свойств в разгруженной конфигурации, b – анизотропный тензор 2-го ранга теплового расширения в K_x, – изменение абсолютной температуры.

Для поликристалла использовались гипотезы, предложенные в работе Тейлора [164], в соответствии с которыми градиент деформации каждого зерна равен макроскопическому градиенту (расширенная гипотеза Фойгта). Для такой модели, подробно рассмотренной в [64], тензор напряжений Коши макроуровня можно записать в виде:

,

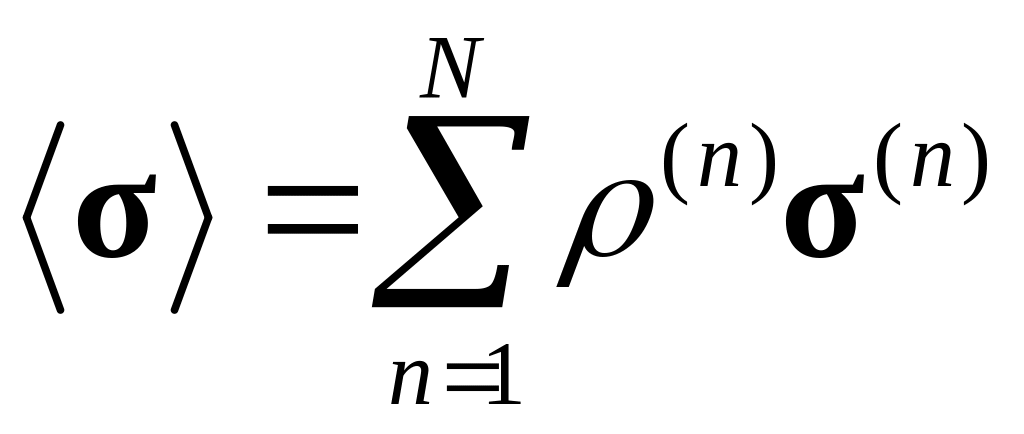где ρ⁽ⁿ⁾ – объемная доля каждого зерна в представительном объеме поликристалла. Принимая все зерна агрегата одинаковыми по объему, тензор напряжений Коши представим:

.

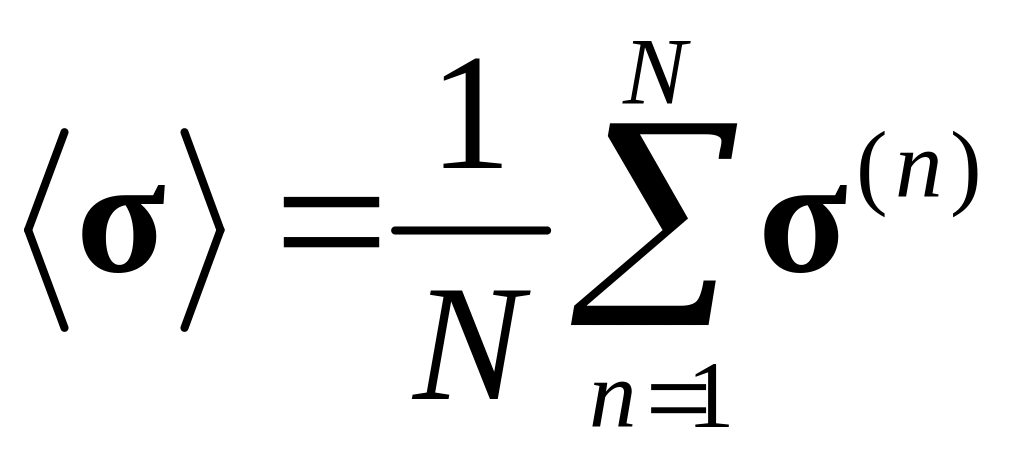Авторы внедрили представленную конститутивную модель в коммерческий конечно-элементный комплекс ABAQUS и провели ряд расчетов для изотермического и адиабатического случаев.