
- •Министерство образования и науки российской федерации
- •Физические теории пластичности
- •Оглавление
- •Основные обозначения
- •Сокращения
- •Введение
- •Подход к построению определяющих соотношений с использованием внутренних переменных
- •Структура конститутивной модели с внутренними переменными
- •О многоуровневых моделях
- •Вопросы к «Введению»
- •Глава 1. Основные понятия и определения
- •1.1. О геометрической нелинейности и независимых от выбора системы отсчета тензорзначных характеристиках
- •1.2. Классический и обобщенные континуумы
- •Вопросы к главе 1
- •Глава 2. Механизмы неупругого деформирования
- •2.1. О дислокационных механизмах неупругого деформирования
- •2.2 Взаимодействия дислокаций с дислокациями и точечными дефектами
- •2.3 Деформирование монокристалла двойникованием
- •2.4. Закон Шмида
- •2.5. Механизмы и модели деформационного упрочнения
- •Вопросы к главе 2
- •Глава 3. Кинематика неупругого деформирования
- •3.1. Уравнение Орована
- •3.2. Моды неупругого деформирования монокристаллов
- •3.3. Статистически накопленные и геометрически необходимые дислокации, изгибы–кручения решетки
- •3.4 Ротационные моды деформирования, модели ротации
- •Вопросы к главе 3
- •Глава 4. Жесткопластические модели
- •4.1. Модель Закса
- •4.2. Модель Тейлора
- •4.3. Модель Бишопа-Хилла
- •Вопросы к главе 4
- •Глава 5. Упругопластические модели
- •5.1. Модель Линя
- •5.2. Направления развития упругопластических моделей
- •Вопросы к главе 5
- •Глава 6. Вязкоупругие и вязкопластические модели
- •Вопросы к главе 6
- •Глава 7. Упруговязкопластические модели
- •7.1 Анализ упруговязкопластических моделей [64, 114]
- •7.2. Краткий обзор работ по упруговязкопластическим моделям
- •Вопросы к главе 7
- •Глава 8. Структура и алгоритмы реализации многоуровневых моделей
- •8.1. Наиболее распространенная схема построения многоуровневых моделей, их структура и классификация
- •8.2. Согласование определяющих соотношений масштабных уровней и конкретизация независящей от выбора системы отсчета производной
- •8.3. Классификация внутренних переменных и уравнений конститутивной модели на примере двухуровневой упруговязкопластической модели
- •8.4. Модель поворотов кристаллической решетки, учитывающая взаимодействие элементов мезоуровня
- •8.5. Алгоритм реализации двухуровневой упруговязкопластической модели
- •Библиографический список
- •Предметный указатель
Вопросы к главе 5
Какие соотношения применяются в качестве определяющих в большинстве физических теорий?
Приведите и проанализируйте основные гипотезы модели Линя.
Приведите кинематические и определяющие соотношения для кристаллита, применяемые в модели Линя.
Изложите алгоритм применения модели Линя для исследования упругопластического деформирования поликристаллического представительного макрообъема.
Перечислите достоинства и недостатки модели Линя.
Какие физические модели применяются для удовлетворения условий равновесия на границах кристаллитов?
Каким образом модифицируется закон Гука в случае геометрически нелинейных задач?
Проанализируйте закон упрочнения, используемый в работах Токуды и Краточвила.
Используя мультипликативное разложение градиента места, получите аддитивное разложение градиента скорости перемещений на упругую и пластическую составляющие.
Запишите определяющие соотношения гипоупругости и гиперупругости.
Глава 6. Вязкоупругие и вязкопластические модели
Наряду с жесткопластическими и упругопластическими моделями физической теории пластичности интенсивно разрабатываются и вязкопластические (вязкоупругие) модели (т.е. модели, в которые явным образом входит физическое время), роль которых особенно велика при рассмотрении процессов неупругого деформирования при повышенных температурах и медленных нагружениях, поскольку, как известно, движение дислокаций (особенно – неконсервативное) является термически активируемым, связанным с диффузионными процессами.
Основным вопросом построения вязких моделей является выбор определяющего соотношения для скоростей сдвигов по СС, которое в таких моделях записывается явным образом. Среди множества таких определяющих соотношений выделим широко используемый (см., например, [63, 64, 105, 145, 149]) степенной закон (часто в литературе называемый соотношением Хатчинсона):
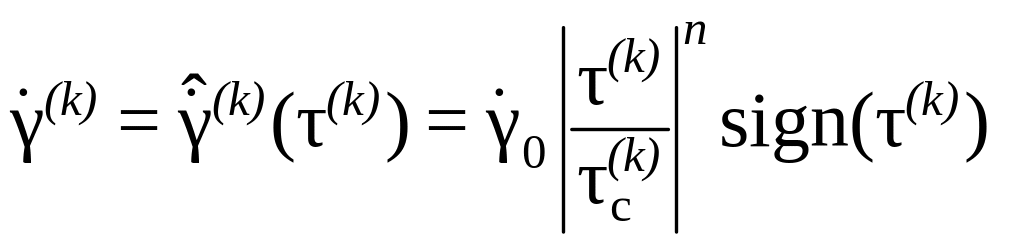 ,
,
где
![]() – критическое напряжение сдвига на k-й
СС; следует отметить, что в
вязкоупругих и вязкопластических
моделях удвоение числа СС не используется,
направление скольжения определяется
знаком сдвигового напряжения.
Следует отметить, что при стремлении
n→∞ соотношение приближается к
жесткопластическому закону; детально
вопрос об эквивалентности вязкопластической
и жесткопластической моделей исследован
в работах [62, 144].
– критическое напряжение сдвига на k-й
СС; следует отметить, что в
вязкоупругих и вязкопластических
моделях удвоение числа СС не используется,
направление скольжения определяется
знаком сдвигового напряжения.
Следует отметить, что при стремлении
n→∞ соотношение приближается к
жесткопластическому закону; детально
вопрос об эквивалентности вязкопластической
и жесткопластической моделей исследован
в работах [62, 144].
Следует отметить, что модели, построенные на соотношении нельзя в полной мере отнести к пластическим, поскольку в явным образом отсутствует пороговость, характерная для пластических моделей. Поэтому модели, построенные на принято называть вязкоупругими, для перехода к вязкопластическим моделям соотношение необходимо модифицировать, например, введя в него функцию Хэвисайда:
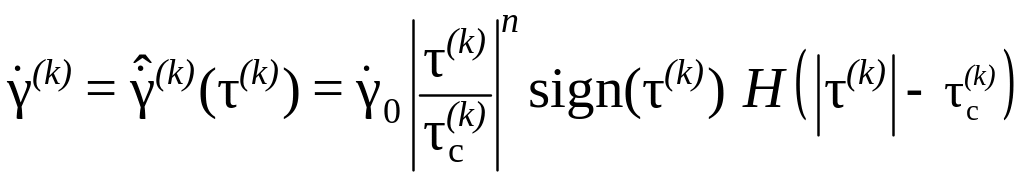 .
.
Кроме того, следует отметить, что в
вязкоупругих моделях не имеет смысла
вводить понятие активности системы
скольжения, т.к. при любых положительных
касательных напряжениях соотношение
Хатчинсона будет давать ненулевую
скорость сдвига, поэтому при анализе
поведения материалов на мезоуровне для
вязкоупругих моделей рассматриваются
накопленные сдвиги на всех потенциально
возможных СС, оценивая в каждый момент
деформирования относительную скорость
сдвигов на различных СС. При этом и
критическое напряжение сдвига
![]() изменяет свой первоначальный смысл,
который оно имело в жесткопластических
и упругопластических моделях как
касательного напряжения начала
скольжения; оно выступает теперь в роли
материальной функции процесса, определение
которой при идентификации модели следует
осуществлять в совокупности с установлением
других параметров вязкоупругого закона
–
изменяет свой первоначальный смысл,
который оно имело в жесткопластических
и упругопластических моделях как
касательного напряжения начала
скольжения; оно выступает теперь в роли
материальной функции процесса, определение
которой при идентификации модели следует
осуществлять в совокупности с установлением
других параметров вязкоупругого закона
–
![]() и
п. Однако физический смысл
как сопротивления движению дислокаций
при этом сохраняется, что позволяет
относительно независимо от других
параметров модели формулировать для
него законы упрочнения.
и
п. Однако физический смысл
как сопротивления движению дислокаций
при этом сохраняется, что позволяет
относительно независимо от других
параметров модели формулировать для
него законы упрочнения.
Весьма противоречивые данные приводятся
в литературе для параметра
,
значения которого по различным источникам
отличаются на 4-5 порядков. С детальным
анализом влияния параметра
на
поведение модели можно ознакомиться в
работе [59], где рассмотрены
характерные особенности вязкопластического
соотношения для определения скоростей
сдвигов. В соответствии с двухуровневой
физической моделью ГЦК-поликристалла
[48] рассмотрен представительный
объем поликристаллического тела с
равномерным случайным распределением
ориентаций кристаллических решеток
отдельных зерен, испытывающий деформацию
одноосного сжатия вдоль одной из осей
неподвижной лабораторной системы
координат; параметры материала
соответствуют чистой меди. Упрочнение
и развороты зерен в статье не
рассматриваются. В качестве определяющего
соотношения для скоростей сдвигов в
отдельных зернах выбрано соотношение
. Выделен параметр
![]() ,
связывающий характерную скорость
деформирования (в процессе с постоянной
скоростью деформации) и
скорость сдвига в СС при достижении
критического касательного напряжения:
,
связывающий характерную скорость
деформирования (в процессе с постоянной
скоростью деформации) и
скорость сдвига в СС при достижении
критического касательного напряжения:
![]() ,
выявлены характерные зависимости от
данного параметра характеристик
напряженно-деформированного состояния.
Показано, что характер диссипации
энергии пластическими сдвигами зависит
от значения
,
точнее: при
,
выявлены характерные зависимости от
данного параметра характеристик
напряженно-деформированного состояния.
Показано, что характер диссипации
энергии пластическими сдвигами зависит
от значения
,
точнее: при
![]() скольжение сдвигом
характеризуется меньшим набором активных
систем скольжения и большими скоростями
сдвигов, при
скольжение сдвигом
характеризуется меньшим набором активных
систем скольжения и большими скоростями
сдвигов, при
![]() – большим количеством
активных СС и меньшими
скоростями сдвигов в них.
Также показано, что суммарная
скорость сдвига по
всем СС не зависит от данного параметра,
а зависит от скорости деформирования.
Выявлена обратная зависимость предела
текучести от
,
однако при значениях
предел текучести одинаков и модель по
сути становится упругопластической.
– большим количеством
активных СС и меньшими
скоростями сдвигов в них.
Также показано, что суммарная
скорость сдвига по
всем СС не зависит от данного параметра,
а зависит от скорости деформирования.
Выявлена обратная зависимость предела
текучести от
,
однако при значениях
предел текучести одинаков и модель по
сути становится упругопластической.
Остановимся на одной из самых простых
моделей вязкого типа [60].
В качестве закона течения принят типовой
закон ; как уже отмечалось выше, этот
закон применяется чрезвычайно часто,
основные отличия теорий вязкого типа
состоят в принимаемых законах упрочнения,
учете (или неучете) влияния температуры,
вводимых в рассмотрение механизмов
деформирования. В цитируемой работе
применен анизотропный закон упрочнения
![]() ,
где hkl – матрица модулей
упрочнения, которую следуя [110]
для ГЦК–кристаллов
предлагается принять в виде:
,
где hkl – матрица модулей
упрочнения, которую следуя [110]
для ГЦК–кристаллов
предлагается принять в виде:
 .
.
Здесь h0, τs, а –
материальные параметры, определяющие
скорость упрочнения (τs – так
называемое напряжение насыщения),
приятые постоянными для всех СС. Матрица
![]() для ГЦК–кристаллов (12 СС)
представляется в блочной форме:
для ГЦК–кристаллов (12 СС)
представляется в блочной форме:
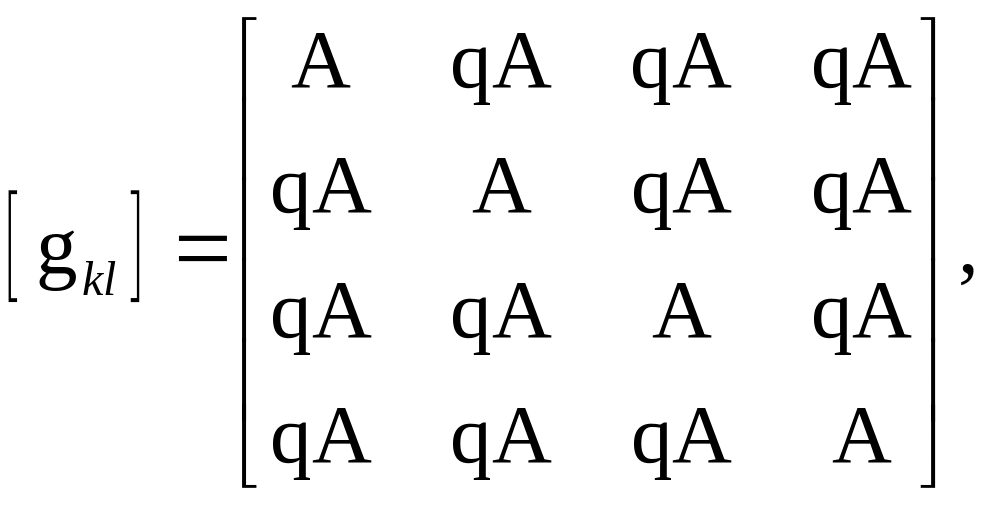
где А – матрицы размерностью 3×3, все компоненты которой равны 1, q – характеризует отношение скорости латентного и деформационного упрочнения. Тензор пластической составляющей градиента скорости перемещений выражается классическим соотношением:
![]() ,
,
где
и
![]() – соответственно симметричная и
несимметричная части фактора Шмида,
,
– соответственно симметричная и
несимметричная части фактора Шмида,
,
![]() .
Тогда тензор пластической
составляющей градиента скорости
перемещений можно
представить в виде суммы скорости
неупругой деформации
.
Тогда тензор пластической
составляющей градиента скорости
перемещений можно
представить в виде суммы скорости
неупругой деформации
![]() и тензора «пластического спина»
и тензора «пластического спина»
![]() .
В силу того, что упругими и термическими
деформациями пренебрегают, определяющее
соотношение для описания вязкопластического
поведения материала принимает вид:
.
В силу того, что упругими и термическими
деформациями пренебрегают, определяющее
соотношение для описания вязкопластического
поведения материала принимает вид:
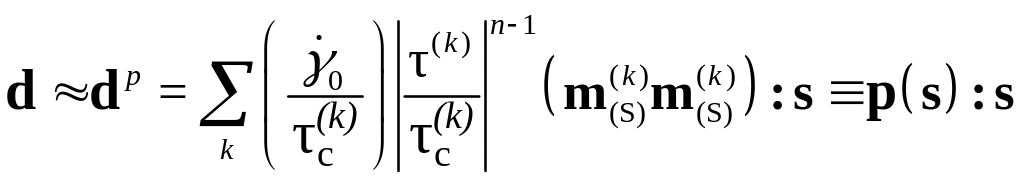 ,
,
где
![]() – так называемый тензор вязкопластических
свойств (4-го ранга), s
– девиатор тензора напряжений Коши.
Показывается, что в случае 5 активных
систем скольжения тензор
обратим, тогда можно разрешить
относительно напряжений:
– так называемый тензор вязкопластических
свойств (4-го ранга), s
– девиатор тензора напряжений Коши.
Показывается, что в случае 5 активных
систем скольжения тензор
обратим, тогда можно разрешить
относительно напряжений:
![]() .
.
В силу пренебрежения в
рассматриваемой работе упругими
деформациями упругая составляющая
градиента места равна ортогональному
тензору,
![]() ,
который полагается ответственным за
повороты кристаллической решетки.
Данная модель в цитируемой работе
используется в сочетании с самосогласованной
схемой, однако использовать ее можно и
в рамках статистического подхода.
,
который полагается ответственным за
повороты кристаллической решетки.
Данная модель в цитируемой работе
используется в сочетании с самосогласованной
схемой, однако использовать ее можно и
в рамках статистического подхода.
Более сложная модификация модели вязкого типа рассмотрена в работе [113], в которой учтено влияние температуры, базирующееся на континуальной модели «механического порогового напряжения» (MTS – mechanical threshold stress), предложенной Фоллансби и Куксом [93]. Последняя представляет собой изотропную «скалярную» модель для предсказания напряжения течения в зависимости от скорости деформации, температуры и текущего состояния, описываемого параметром состояния, называемым механическим порогом. В первой части работы рассматривается так называемая «стандартная вязкопластическая модель Тейлора» (standard rate dependent Taylor model). В ней используется «жесткопластическое» мультипликативное разложение градиента места f:
![]() .
.
Составляющая переводит отсчетную конфигурацию К0 в промежуточную при отсутствии поворота (ориентация кристаллической решетки остается неизменной), а ротация r переводит в актуальную конфигурацию Кt. Тогда (транспонированный) градиент скорости перемещений l (в актуальной конфигурации) определяется соотношением:
![]() .
.
Заметим, что
![]() – «пластический» градиент скорости
перемещений, связанный со скоростями
сдвигов по системам скольжения (СС)
соотношением:
– «пластический» градиент скорости
перемещений, связанный со скоростями
сдвигов по системам скольжения (СС)
соотношением:
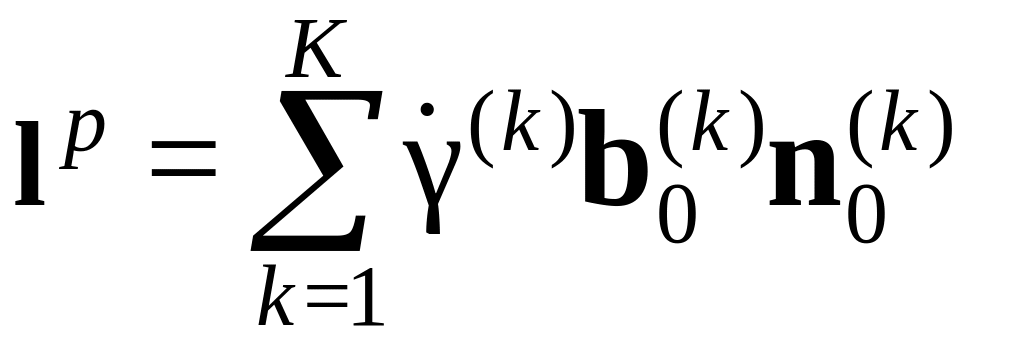 ,
,
где
![]() – скорость сдвига по k-й
СС,
– скорость сдвига по k-й
СС,
![]() –
единичный вектор направления скольжения
(сонаправленный вектору Бюргерса),
–
единичный вектор направления скольжения
(сонаправленный вектору Бюргерса),
![]() –
единичный вектор нормали k-й
СС, определенные в промежуточной (или,
что то же самое, в отсчетной) конфигурации.
Вводится аддитивное разложение градиента
скорости перемещений:
–
единичный вектор нормали k-й
СС, определенные в промежуточной (или,
что то же самое, в отсчетной) конфигурации.
Вводится аддитивное разложение градиента
скорости перемещений:
![]() ,
,
при этом с учетом – имеем:
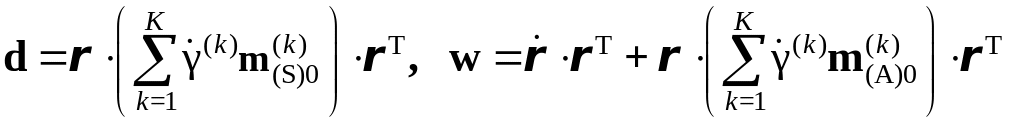 ,
,
где
![]() .
Тензор ротации решетки определяется
решением уравнения:
.
Тензор ротации решетки определяется
решением уравнения:
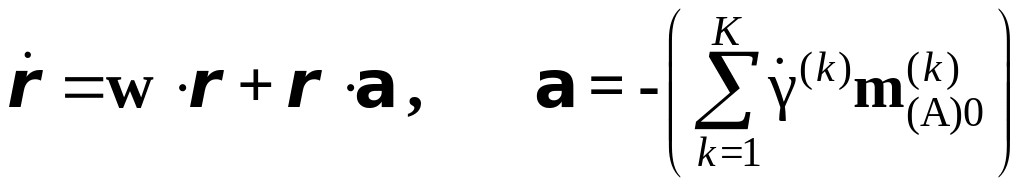 .
.
Таким образом, ротация решетки складывается
из «материального вращения» (w)
и ротации от «стесненного
сдвига» (a).
Используя далее симметричный
ориентационный тензор в актуальной
конфигурации
(![]() ),
сдвиговое напряжение в k-й
СС устанавливается следующим образом:
),
сдвиговое напряжение в k-й
СС устанавливается следующим образом:
![]() ,
,
где
![]() – тензор напряжений Коши и его девиатор
(мезоровня).
– тензор напряжений Коши и его девиатор
(мезоровня).
Подставляя в 1, девиатор напряжений может быть определен решением следующей системы нелинейных уравнений:
![]() ,
,
где четырехвалентный тензор вязкопластических свойств определяется соотношением:
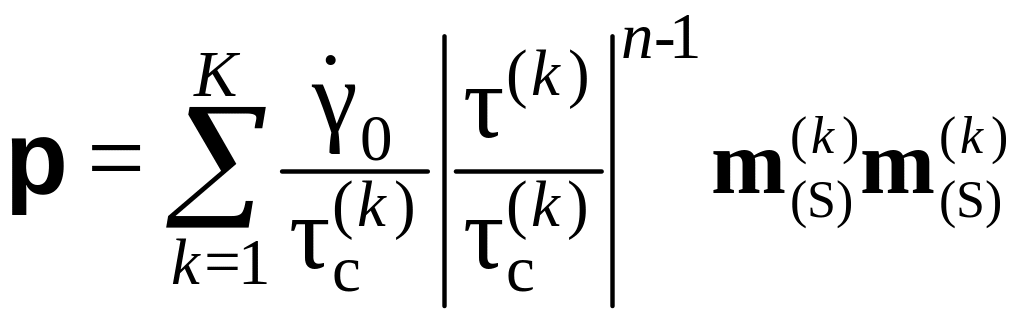 ,
,
т.е. идентичен использованному в
соотношении . Следует подчеркнуть, что
из определения тензора свойств
![]() очевидна нелинейность соотношения ,
поскольку
очевидна нелинейность соотношения ,
поскольку
![]() определяется по искомому тензору s.
определяется по искомому тензору s.
Принимается закон изотропного упрочнения, эволюционное уравнение для критического напряжения имеет вид закона Воуса (Voce):
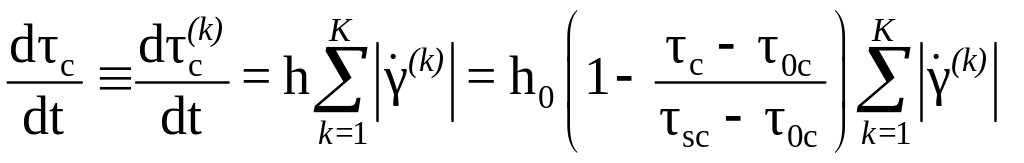 .
.
Здесь h0 – начальная
скорость упрочнения,
![]() – начальное напряжение течения и
напряжение насыщения. Макроскопический
девиатор напряжений определяется
осреднением с весами по всем зернам.
– начальное напряжение течения и
напряжение насыщения. Макроскопический
девиатор напряжений определяется
осреднением с весами по всем зернам.
Отмечается, что степенной закон может рассматриваться лишь как приближенный закон, не имеющий под собой должного физического обоснования. В связи с этим в работе предлагается модифицировать указанный закон для учета скорости деформации в широком диапазоне ее варьирования и влияния температуры. В основу указанной модификация положена упомянутая выше модель механического порогового напряжения.
Подробно описывается численная процедура; для интегрирования по времени используется неявная разностная схема, система нелинейных уравнений решается методом Ньютона–Рафсона. Для установления шага по времени решена задача на одноосное сжатие при 10, 20, 40 и 100 постоянных шагах по времени; различие между результатами расчета напряжения сжатия при 10 и 100 шагах не превысило 0.24%.
Верификация предлагаемой модели осуществляется сопоставлением полученных с ее помощью результатов расчета напряжений с результатами стандартной изотропной модели MTS. Скоростная и температурная зависимости определялись в опытах на сжатие алюминиевого сплава Al 5182 при температурах 200 и 300оС при скоростях деформации 0.001 и 1.0 с-1. Показано очень хорошее соответствие результатов. Анализ предсказания моделью формирования текстуры осуществлен сопоставлением с результатами, полученными Kalidindi e.a. с использованием модели Тейлора; отмечается хорошее качественное соответствие результатов.
В работе [141] также
используется мультипликативное
разложение градиента места. Упругими
деформациями пренебрегается, в силу
чего упругая составляющая градиента
места описывает только поворот
кристаллической решетки,
![]() .
Получено аддитивное разложение градиента
скорости перемещений l в промежуточной
конфигурации:
.
Получено аддитивное разложение градиента
скорости перемещений l в промежуточной
конфигурации:
![]() ,
,
где
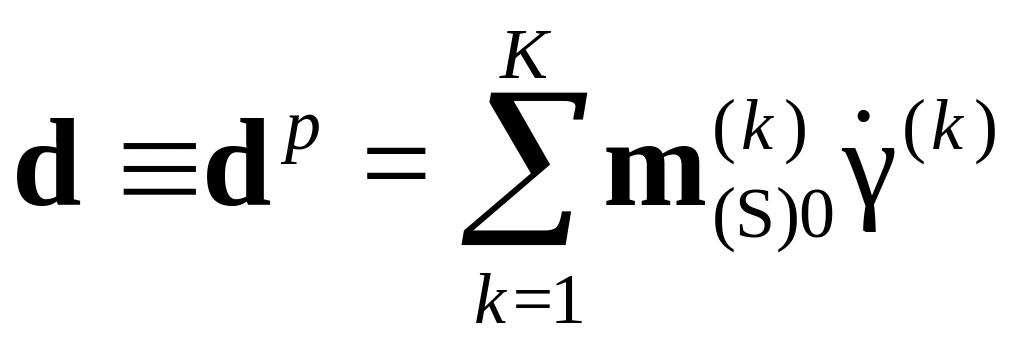 ,
,
![]() – спин решетки,
– спин решетки,
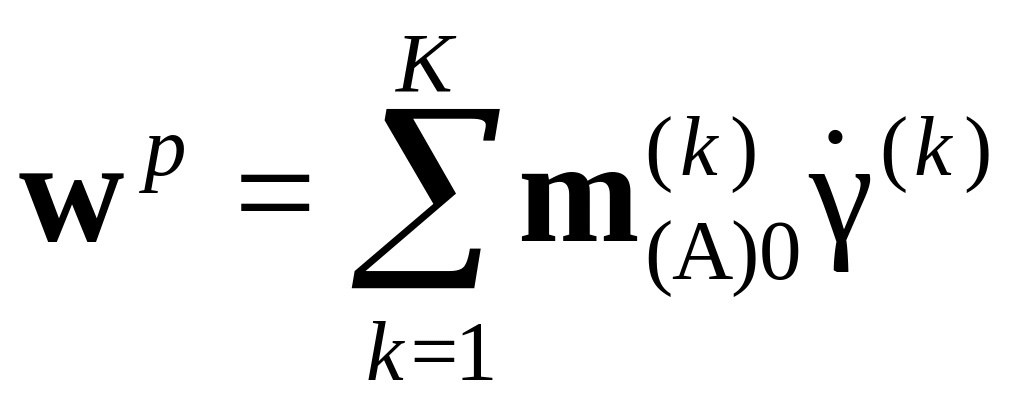 ,
причем тензоры
,
причем тензоры
![]() и
и
![]() (симметричная
и антисимметричная части ориентационного
тензора) определены также в промежуточной
конфигурации. Используется гипотеза
Фойгта, т.е. деформации скорости
принимаются одинаковыми в каждый момент
времени во всех зернах поликристалла.
Скорости сдвигов на СС определяются
степенным законом вида .
(симметричная
и антисимметричная части ориентационного
тензора) определены также в промежуточной
конфигурации. Используется гипотеза
Фойгта, т.е. деформации скорости
принимаются одинаковыми в каждый момент
времени во всех зернах поликристалла.
Скорости сдвигов на СС определяются
степенным законом вида .
Следует отметить, что хотя в вязкопластических
моделях активными в каждый момент
времени могут быть любые из возможных
для данного типа кристалла СС, не все
они будут линейно независимы; например,
на каждой кристаллографической плоскости
линейно независимыми могут быть только
две из трех СС. В работе предлагается
эвристическая, чисто геометрическая
процедура определения активных СС,
число которых на каждой плоскости не
более двух; например, для ГЦК – кристаллов
общее число активных СС, таким образом,
не превышает восьми. При
определении скоростей
сдвигов на СС используется
принцип минимума сдвига, решается
соответствующая задача оптимизации;
кинематическое ограничение
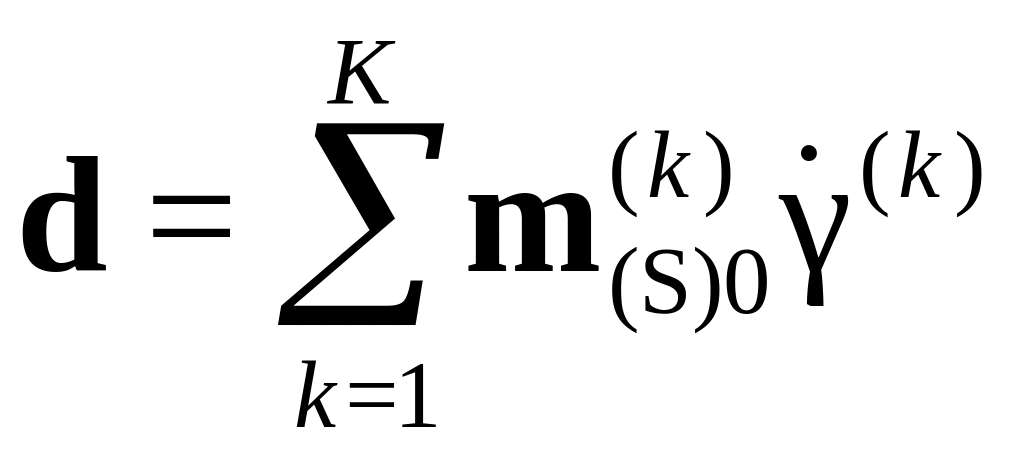 вносится с использованием
множителей Лагранжа.
вносится с использованием
множителей Лагранжа.
С использованием предлагаемой модели решены тестовые задачи одноосной осадки и простого сдвига монокристаллов с различной начальной ориентацией, одноосной осадки, осадки в условиях плоско-деформированного состояния и простого сдвига поликристаллических образцов. Сопоставление результатов расчета эволюции ориентаций кристаллитов с теоретическими результатами, полученными с использованием других моделей, и экспериментальными данными обнаруживает хорошее соответствие.
Представляется целесообразным упомянуть работу [69], содержащей значительное количество экспериментальных данных по лучевым и двухзвенным траекториям деформации листового алюминиевого сплава, пригодных для идентификации и верификации теоретических моделей. Подробно описана методика экспериментальных исследований, включающих как чисто механические измерения, так и анализ текстуры и дислокационных субструктур. Теоретические исследования проведены с использованием вязкопластических моделей со степенным законом, «полностью стесненной» и самосогласованной. Обе модели дают близкие результаты как по зависимостям напряжений от работы на пластических деформаций, так и по полюсным фигурам; отмечается, что полюсные фигуры в теоретических расчетах получаются более четко выраженными («острыми»), чем в экспериментах.
